|
||||
|
Глава 1 Справочная информация теоретического характера § 1. Логические основы школьного курса планиметрии 1.1. Справочная информация Геометрия – это наука о свойствах геометрических фигур. Слово «геометрия» греческое, в переводе на русский язык означает «землемерие». Такое название этой науке было дано потому, что в древнее время главной целью геометрии было измерение расстояний и площадей на земной поверхности. Геометрия часто применяется на практике. Её надо знать и рабочему, и инженеру, и архитектору, и художнику. Одним словом, геометрию надо знать всем. Планиметрия – это раздел геометрии, в котором изучаются фигуры на плоскости. Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур. Основными геометрическими фигурами на плоскости являются точка и прямая. Этим фигурам в геометрии не даётся определений. Также не определяются такие понятия (отношения), как «лежать между», «принадлежать», «проходить через...» и так далее. Остальным геометрическим фигурам и другим понятиям даются определения. Определение – это предложение, в котором разъясняется смысл и содержание того или иного понятия. При этом разъяснение состоит в том, что оно сводится к ранее определённым понятиям. Существует несколько подходов к построению курса планиметрии (и геометрии в целом):аксиоматический, аналитический, векторный, групповой. Аксиоматическая теория строится следующим образом: 1) даются неопределяемые понятия (в нашем случае это точка и прямая); 2) вводятся неопределяемые отношения (связи между понятиями – «лежать между», «принадлежать» и так далее); 3) даётся система аксиом – то есть утверждений, принимаемых без доказательства; 4) на основе аксиом и законов математической логики доказываются теоремы. Аксиом, как правило, немного, а вот теорем – бесконечное множество. К аксиомам планиметрии можно отнести следующие: 1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну. 2. Из трёх точек на данной прямой одна и только одна лежит между двумя другими. 3. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин его частей, на которые он разбивается любой его точкой. 4. Прямая разбивает плоскость на две полуплоскости. 5. Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами. 6. На любом луче от его начальной точки можно отложить отрезок заданной длины, и только один. 7. От любого луча в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один. 8. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данного луча. 9. Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной. На основе приведённых аксиом доказываются различные свойства геометрических фигур (теоремы). Доказать теорему – значит провести логически правильное рассуждение о свойстве той или иной геометрической фигуры. Любая теорема состоит из двух частей: условия и заключения. Записывают это так: У ? З (из условия следует заключение; или: если У, то З). Например: У = «углы ? и ? – вертикальные», З = «углы ? и ? равны». Получаем верное утверждение (теорему):У ? З (если углы и – вертикальные, то они равны, или, проще: вертикальные углы равны). К каждому утверждению У ? З, называемому прямым, можно написать ещё три: З ? У – обратное утверждение; не У ? не З – противоположное утверждение; не З ? не У – противоположное к обратному утверждение. В нашем примере обратное утверждение (если углы равны, то они вертикальны) и противоположное утверждение (если углы не вертикальные, то они не равны) являются ложными, а вот противоположное к обратному утверждение (если углы не равны, то они не вертикальные) – истинно. Вообще, в математической логике есть закон контрапозиции, который гласит, что прямое и противоположное к обратному утверждения эквивалентны (по этому же закону эквивалентны обратное и противоположное утверждения). На законе контрапозиции основан метод доказательства теорем от противного. Пусть требуется доказать теорему У ? З. Мы предполагаем, что её заключение неверно. Далее логически доказываем, что тогда и У неверно. Иными словами, мы доказываем противоположную к обратной теореме: не З ? не У. Тогда прямая теорема по закону контрапозиции также верна. Метод доказательства от противного применяется тогда, когда противоположная к обратной теорема доказывается проще прямой теоремы. Теоремы можно поделить и по другому основанию. Выделяют теоремы-свойства и теоремы-признаки. В теоремах-свойствах доказываются свойства заданных геометрических фигур. Например, утверждение: «в ромбе диагонали перпендикулярны друг другу», «медианы в треугольнике делятся в отношении 2:1» – это теоремы свойства. Теоремы-признаки – это утверждения, благодаря которым можно определить, о какой фигуре идет речь. Например, «если в четырёхугольнике противоположные стороны равны, то этот четырёхугольник – параллелограмм». Безусловно, верно и обратное утверждение: «у параллелограмма противоположные стороны равны». Иными словами, равенство противоположных сторон является не только свойством, но и признаком параллелограмма. Свойство фигуры, которое является одновременно и её признаком, называется характеристическим свойством (критерием) данной геометрической фигуры. В принципе, любое характеристическое свойство фигуры можно принять за её определение. Иногда для удобства выделяют два частных случая теорем – следствие и лемму. Следствие – это утверждение, непосредственно вытекающее из теоремы. Лемма – это вспомогательное утверждение, используемое при доказательстве основной теоремы. Множество всех неопределяемых понятий и отношений, аксиом и теорем называют аксиоматической теорией. Аксиоматическая теория, построенная на основе девяти приведённых аксиом, называется евклидовой. Несколько дополнительных сведений по аксиоматическому подходу в геометрии. Система аксиом геометрии подбирается не произвольным образом. К ней предъявляются три основных требования: независимости, непротиворечивости и полноты. Система аксиом называется независимой, если ни одну из аксиом нельзя вывести как теорему из других аксиом (тогда данная аксиома была бы лишней). Система аксиом называется непротиворечивой, если из неё нельзя вывести две теоремы, которые противоречат друг другу. Систему аксиом называют полной, если какое бы утверждение о свойстве той или иной геометрической фигуры мы ни сформулировали, всегда можно установить – истинно оно или ложно. Приведённая выше система аксиом евклидовой геометрии удовлетворяет всем трём требованиям (доказано А. В. Погореловым). Помимо евклидовой существуют и другие аксиоматические теории (неевклидовы геометрии). Например, если девятую аксиому евклидовой геометрии заменить на её отрицание («Через точку, не лежащую на прямой, можно провести более одной прямой, параллельной данной»), а остальные оставить без изменения, получим планиметрию Лобачевского. Тогда будут доказаны неожиданные для нас утверждения: «Сумма углов в треугольнике меньше двух прямых», «существуют треугольники, около которых нельзя описать окружность», «не существует подобных треугольников» и многие другие. Изменяя систему аксиом, а также меняя неопределяемые понятия и отношения, мы будем получать другие неевклидовы геометрии (сферическую, эллиптическую и так далее). Помимо аксиоматического, в геометрии широко распространён аналитический подход. Его суть состоит в том, что на плоскости вводится система координат и каждой точке ставится в соответствие пара чисел (х; у) – её координаты. Благодаря этому удаётся записывать уравнения различных фигур (прямых, окружностей и так далее), изучать их свойства. Введение декартовой прямоугольной системы координат и применение алгебраического аппарата нередко позволяют легче решать многие задачи по геометрии. Обобщением (в определённом смысле) аналитического подхода в геометрии является векторный подход. Разница состоит в том, что на плоскости вводится векторная (аффинная) система координат, причём два базисных вектора не обязательно перпендикулярны друг другу и к тому же могут различаться по длине. Введение векторной системы координат также нередко позволяет быстрее и проще решать целый ряд геометрических задач. В высшей геометрии весьма распространён групповой подход. Группой называется непустое множество М, на котором определена некоторая операция*, причём выполняются следующие условия: 1) для любых элементов а, в, с из М(а*в)*с = а*(в*с): 2) существует элемент е из М, такой, что а*е = е*а = а: 3) для любого элемента а существует элемент а-1, что а*а-1= а-1*а = е. В геометрии можно выделить множество групп, например, группу перемещений, группу преобразования подобия. Самой важной группой в планиметрии является группа перемещений плоскости, так как с её помощью вводится понятие равных фигур. Равные фигуры обладают одинаковыми геометрическими свойствами, которые не изменяются (инвариантны) под действием перемещений. В целом можно сказать, что каждая группа преобразований задаёт свою геометрию, в которой изучаются свойства фигур, инвариантные (неизменяемые) относительно данной группы преобразований. Инварианты группы перемещений (и других групп) «невидимо» присутствуют при решении задач методом геометрических преобразований. Так, строя образы фигур при различных видах движений (симметрия, параллельный перенос и так далее), мы получаем равные фигуры, что позволяет в ряде случаев успешно решать сложные задачи. 1.2. Вопросы для самопроверки 1. Что изучает геометрия? (1) 2. Что означает слово «геометрия» в переводе с греческого языка? (1) 3. В каких видах человеческой деятельности нужны знания по геометрии и пространственное воображение? Покажите эту значимость в деятельности: а) рабочего; б) инженера; в) архитектора; r) художника; д) Вас лично в решении бытовых задач. (1) 4. Что изучает планиметрия? Приведите примеры геометрических фигур и их свойств. (1) 5. Назовите основные (неопределяемые) понятия в планиметрии. (1) 6. Какие вы знаете неопределяемые отношения в курсе геометрии? (1) 7. Что значит дать определение геометрической фигуры? (1) 8. В чем состоит сущность аксиоматического подхода в геометрии? (1) 9. Что такое аксиома? (1) 10. Что такое теорема? (1) 11. Перечислите аксиомы планиметрии. (1) 12. Что значит доказать теорему? (1) 13. Из каких частей состоит теорема? (1) 14. Какая теорема называется: а) обратной; б) противоположной; в) противоположной к обратной? (1) 15. Даны четыре теоремы: прямая, обратная, противоположная, противоположная к обратной. Какие пары из перечисленных теорем являются эквивалентными? (1–2) 16. В чем состоит сущность метода доказательства теорем от противного? (1) 17. Что такое теорема-свойство и теорема-признак? (1) 18. Что такое характеристическое свойство геометрического объекта (фигуры, тела и т. д.)? Как связаны между собой термины «характеристическое свойство объекта» и «определение объекта»? (1) 19. Какие требования предъявляются к системе аксиом? (3) 20. Как вы понимаете следующие высказывания: а) система аксиом непротиворечива; (3) б) система аксиом независима; (3) в) данная система аксиом – полная (3)? 21. Какая геометрия называется евклидовой? (1) 22. Какие неевклидовы геометрии вы знаете? (3) 23. В чем отличие аксиоматики Лобачевского от систем аксиом Евклида? (3) 24. В чем суть аналитического подхода в геометрии? (2) 25. Что такое аффинная система координат? (2) 26. Что такое группа? В чем суть группового подхода в геометрии? (3) 27. Что такое инвариант? (3) 1.3. Темы для сообщений и рефератов 1. Высказывания. Операции над высказываниями. Законы математической логики.(2) 2. Основные факты планиметрии Лобачевского. (3) 3. Особенности геометрии на сфере. (3) 4. Методы доказательства теорем (прямое доказательство, от противного, контрпример, метод симметрии и т. д.). (1–2) 5. Группы преобразований плоскости и их инварианты. (3) 6. Топологические многообразия в геометрии. (3) § 2. Основные понятия планиметрии 2.1. Справочная информация На экзамене по геометрии очень важно давать правильные (корректные) определения. Часто допускаются такие ошибки, как «порочный круг» (например, круг – это часть плоскости, ограниченной окружностью, а окружность – это граница круга), наличие синонима определяемого термина в определении, пропуск «несущественных деталей» (например, касательная к окружности – это прямая, имеющая с окружностью одну общую точку, «деталь» – это тот факт, что прямая должна лежать с окружностью в одной плоскости). Определения геометрических фигур можно дать различными способами: 1. Через род и видовое отличие. Например: квадрат – это прямоугольник с равными сторонами. Прямоугольник в определении – ближайший род, равенство сторон – видовое отличие. 2. Генетически (указание происхождения понятия). Например, окружность – это множество точек плоскости, находящихся на равном расстоянии от данной точки, лежащей в этой плоскости. 3. Через указание свойств фигуры (дескрипции). Пример: число ? – это то число, которое, будучи умножено на длину диаметра, даёт длину его окружности. 4. Конструктивно (указывается способ построения объекта). Пример: пусть дана произвольная окружность. Разделим её на n равных частей последовательно расположенными точками А1, А2..., Ап. Замкнутая ломаная A1A2...АnА1 образует правильный n-угольник. 5. Аксиоматически. К примеру, определение площади фигуры F даётся как числовая функция S(F), удовлетворяющая определённым условиям (аксиомам). Другие способы дачи определений в геометрии встречаются крайне редко. Перейдём к определениям. Неопределяемыми геометрическими фигурами на плоскости являются точка и прямая. Точки принято обозначать прописными латинскими буквами: А, В, С, D .... Прямые обозначаются строчными латинскими буквами: а, b, с, d .... Точка А лежит на прямой а, точка В лежит на прямой b, точка О принадлежит одновременно прямым а и b, т. е. является точкой пересечения этих прямых (рис. 1). 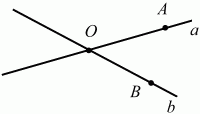 Рис. 1. Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти две точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: «отрезок АВ», то подразумевают отрезок с концами в точках А и В (рис. 2).  Рис. 2. [АВ] – отрезок АВ. Прямая разбивает плоскость на две полуплоскости. Это разбиение обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую. Отрезок АВ не пересекает прямую а, отрезок АС пересекает прямую а (рис. 3). 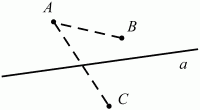 Рис. 3. Лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой луча. Различные лучи одной и той же прямой, имеющие общую начальную точку, называют дополнительными (рис. 4).  Рис. 4. Лучи, так же как и прямые, обозначаются строчными латинскими буквами. Точка А является начальной точкой двух лучей p и q. Лучи p и q являются дополнительными. Углом называется фигура, которая состоит из точки – вершины угла – и двух различных лучей или отрезков, исходящих из этой точки – сторон угла. Слово «угол» иногда заменяют знаком ? (рис. 5, 6). 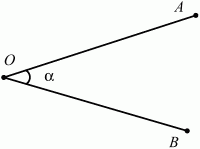 Рис. 5. 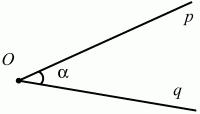 Рис. 6. На рис. 5 угол ? = ?АОВ образован двумя отрезками ОА и ОВ. На рис. 6 угол ? образован двумя лучами р и q, имеющими начальную точку О. Если стороны угла являются дополнительными лучами одной прямой, то угол называют развёрнутым (рис. 7).  Рис. 7. Угол А является здесь развёрнутым. Луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок, соединяющий любые две точки, лежащие на разных сторонах угла. Луч q проходит между сторонами ОА и OB угла AOB (рис. 8). 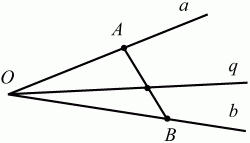 Рис. 8. Углы измеряют в градусах и радианах. При этом ? радиан = 180°. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами (рис. 9). 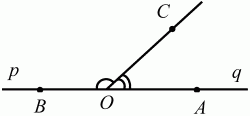 Рис. 9. Сумма смежных углов равна 180°. Лучи p и q – дополнительные, точка В принадлежит лучу p а точка А принадлежит лучу q. Углы СОА и СОВ – смежные. Угол, равный 90°, называется прямым. Угол, меньший 90°, называют острым углом. Угол, больший 90° и меньший 180°, называют тупым (рис. 10, а; б; в). 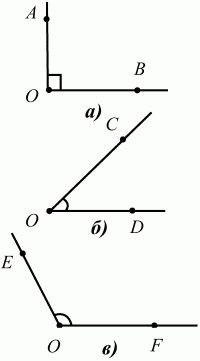 Рис. 10. Углы:?АОВ – прямой, ?COD – острый, ?EOF – тупой. На рисунках прямые углы часто обозначают знаками ?, ?. Два угла называют вертикальными, если стороны одного угла являются дополнительными лучами сторон другого (рис. 11). 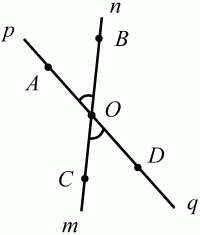 Рис. 11. р и q – дополнительные лучи одной прямой, а m и n – дополнительные лучи другой прямой. Точка О – точка пересечения этих двух прямых и является начальной точкой всех указанных выше лучей. Точки А, В, С, D лежат на соответствующих лучах. Углы АОВ и COD – вертикальные. Две прямые называют перпендикулярными, если они пересекаются под прямым углом. Перпендикулярность прямых обозначается знаком ? (рис. 12): а ? b. 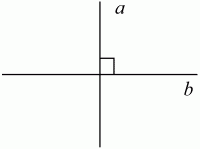 Рис. 12. Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра (рис. 13): АA' – перпендикуляр к прямой a, A' – обоснование перпендикуляра. 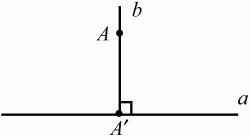 Рис. 13. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам (рис. 14). 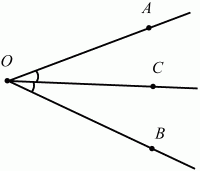 Рис. 14. ОС – биссектриса угла АОВ (?АОС = ?ВОС). Пусть две прямые a и b пересечены прямой с. Прямая с по отношению к прямым a и b называется секущей (рис. 15). 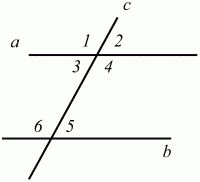 Рис. 15. Углы 3 и 5 (4 и 6) называются внутренними накрест лежащими, углы 3 и 6 (4 и 5) – внутренними односторонними, углы 1 и 6 (2 и 5) – соответственными. Две прямые называются параллельными, если они не пересекаются. Для обозначения параллельности прямых используется знак||(рис. 16): а||b.  Рис. 16. Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами (рис. 17): ?ABC. 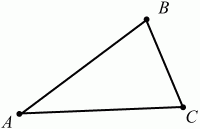 Рис. 17. Углом треугольника ABC при вершине А называется угол, образованный отрезками АВ и АС. Также определяются углы треугольника при вершинах В и С. Две фигуры называются равными, если они при наложении друг на друга совпадают (т. е. существует движение, переводящее одну фигуру в другую). Таким образом, треугольники равны, если у них соответствующие стороны и соответствующие углы равны (при этом соответствующие углы лежат против соответствующих сторон). Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника (рис. 18). 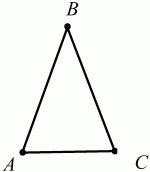 Рис. 18. ?ABC – равнобедренный (АВ = ВС – боковые стороны, АС – основание). Треугольник, у которого все стороны равны, называется равносторонним (рис. 19). 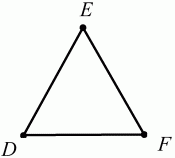 Рис. 19. ? DEF– равносторонний (DE = EF = DF). Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведённый из этой вершины к прямой, которая содержит противолежащую сторону треугольника (рис. 20, а; б). 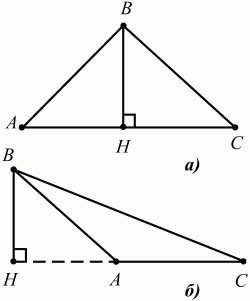 Рис. 20. ВН – высота в треугольнике ABC (ВН ? АС). Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне (рис. 21). 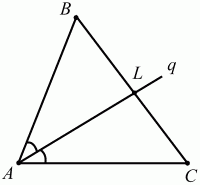 Рис. 21. AL – биссектриса в треугольнике ABC (?BAL = ?CAL). Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны треугольника (рис. 22). 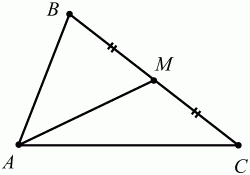 Рис. 22. AM – медиана треугольника ABC (BM = MC). Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине (рис. 23). 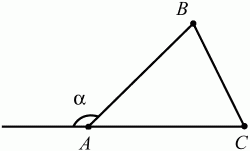 Рис. 23. ? – внешний угол ?ABC при вершине А. Треугольник называется прямоугольным, если у него есть прямой угол (рис. 24). 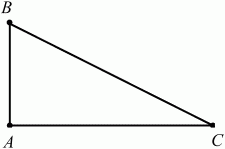 Рис. 24. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами. ?ABC – прямоугольный (?А = 90°). АВ и АС – катеты, ВС – гипотенуза. Треугольник называется остроугольным, если все его углы – острые. Треугольник называется тупоугольным, если у него есть тупой угол. ?ABC – остроугольный, ?А < 90° (рис. 25, а); ?ABC – тупоугольный, ?А > 90° (рис. 25, б). 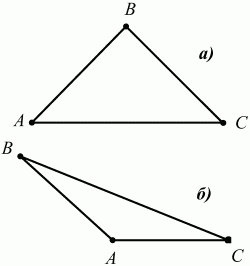 Рис. 25. Средней линией треугольника называется отрезок, соединяющий середины двух любых сторон треугольника (рис. 26). 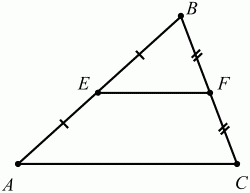 Рис. 26. EF – средняя линия ?ABC (АЕ = ЕВ. CF = FB). Египетским называется прямоугольный треугольник, у которого длины сторон выражаются целыми числами (например:3, 4, 5 или 5, 12, 13 и так далее). Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от заданной точки. Эта заданная точка называется центром окружности. Расстояние от точек окружности до её центра называется радиусом окружности. Радиусом называется также отрезок, соединяющий любую точку окружности с её центром (рис. 27). 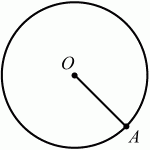 Рис. 27. ОА – радиус окружности. Радиусы окружностей часто обозначают буквами R или r, т. е. ОА = R или ОА = r. Круг – это часть плоскости, ограниченная окружностью (рис. 28).  Рис. 28. Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называется диаметром окружности (рис. 29). 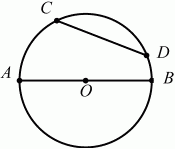 Рис. 29. АВ – диаметр окружности, CD – хорда. Диаметры окружностей часто обозначают буквами D или d. Очевидно, что D = 2R или d = 2 r. Дуга окружности – это её часть, ограниченная двумя точками окружности (рис. 30). 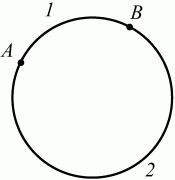 Рис. 30. Точки А и В делят окружность на две дуги:1 и 2. Сектор круга – часть круга, ограниченная двумя радиусами и соответствующей дугой (рис. 31). 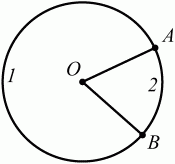 Рис. 31. Радиусы ОА и ОВ разделили круг на два сектора:1 и 2. Сегмент круга – это часть круга, ограниченная хордой и соответствующей дугой (рис. 32). 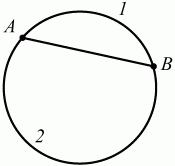 Рис. 32. Хорда АВ делит круг на два сегмента:1 и 2. Окружность называется описанной около треугольника, если она проходит через все его вершины (рис. 33). 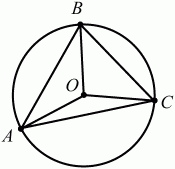 Рис. 33. ОА = ОВ = ОС = R. Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром (рис. 34). В связи с этим говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника. а – серединный перпендикуляр к отрезку АВ (АО = ОВ). 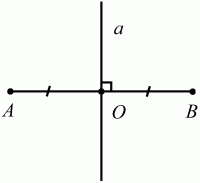 Рис. 34. Прямая, проходящая через точку окружности в той же плоскости перпендикулярно к радиусу, проведённому в эту точку, называется касательной. При этом данная точка окружности называется точкой касания (рис. 35). 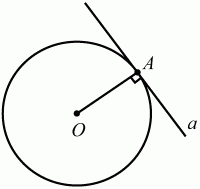 Рис. 35. а – касательная к окружности, А – точка касания, а ? ОА. Говорят, что две окружности, имеющие общую точку, касаются в этой точке, если они имеют в этой точке общую касательную. Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной. Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной (рис. 36, а; б). 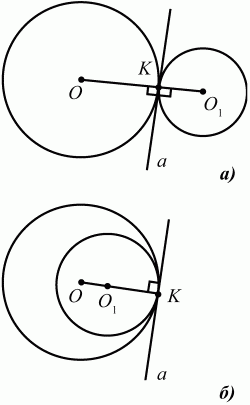 Рис. 36. а – общая касательная к двум окружностям, К – точка касания. Окружность называется вписанной в треугольник, если она касается всех его сторон (рис. 37). 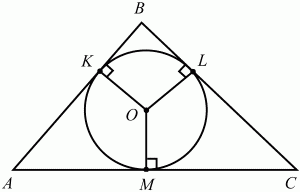 Рис. 37. Точки K, L, M – это точки касания окружности, вписанной в ?ABC. OK = OL = OM = r. В задачах на построение речь идет о построении геометрической фигуры с помощью данных чертёжных инструментов. Такими инструментами чаще всего являются линейка и циркуль. Решение задачи состоит не столько в построении фигуры, сколько в решении вопроса о том, как это сделать, и соответствующем доказательстве. Задача считается решённой, если указан способ построения фигуры и доказано, что в результате выполнения указанных построений действительно получается фигура с требуемыми свойствами. С помощью линейки, как инструмента геометрических построений, можно провести произвольную прямую; произвольную прямую, проходящую через данную точку; прямую, проходящую через две данные точки. Никаких других операций выполнить линейкой нельзя. В частности, нельзя откладывать линейкой отрезки, даже если на ней имеются деления. Циркуль, как инструмент геометрических построений, позволяет описать из данного центра окружность определенного радиуса. Циркулем также можно отложить определенный отрезок на данной прямой от заданной точки. Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, обладающих определённым свойством. Например, окружность можно определить как геометрическое место точек плоскости, равноудалённых от данной точки. Сущность метода геометрических мест, используемого при решении задач, состоит в следующем. Пусть, решая задачу, нам надо найти точку X, удовлетворяющую двум условиям. Геометрическое место точек, удовлетворяющих первому условию, есть некоторая фигура F1, а геометрическое место точек, удовлетворяющих второму условию, есть некоторая фигура F2. Искомая точка X принадлежит F1 и F2 т. е. является их точкой пересечения. Если эти геометрические места простые (скажем, состоят из прямых и окружностей), то мы можем их построить и найти интересующую нас точку X. Ломаной А1А2А3...An называется фигура, которая состоит из точек А1, А2 ..., An и соединяющих их отрезков А1A2, A2A3, ..., An-1, Aп. ТочкиА1, А2..., Аn называются вершинами ломаной, а отрезки A142, A2A3 ..., An-1, An – звеньями ломаной. Ломаная называется простой, если она не имеет самопересечений (рис. 38). 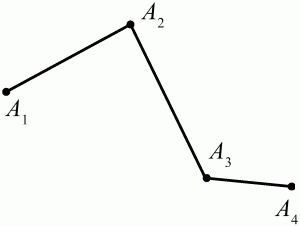 Рис. 38. А1A2A3A4 – простая ломаная из трёх звеньев. Ломаная называется замкнутой, если у неё концы совпадают. Простая замкнутая ломаная называется многоугольником, если её соседние звенья не лежат на одной прямой. Вершины ломаной называются вершинами многоугольника, а звенья ломаной – сторонами многоугольника. Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями. Многоугольник с n-вершинами, а значит, и с n-сторонами называется n-угольником. Плоским многоугольником и многоугольной областью называется конечная часть плоскости, ограниченная многоугольником. Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону (рис. 39). Многоугольник называется невыпуклым, если он оказывается лежащим по обе стороны прямой, содержащей любую его сторону (рис. 40). 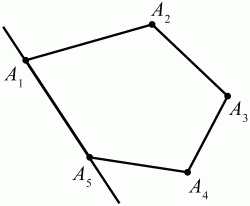 Рис. 39. 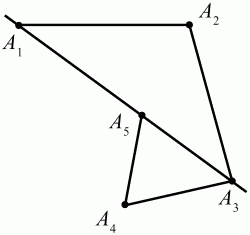 Рис. 40. Выпуклый многоугольник называют правильным, если у него все стороны равны и все углы равны. Многоугольник называется вписанным в окружность, если все его вершины лежат на некоторой окружности. Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности. Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины многоугольника, называются диагоналями. Стороны многоугольника, исходящие из одной вершины, называются соседними сторонами. Стороны, не имеющие общего конца, называются противолежащими сторонами. Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны, т. е. лежат на параллельных прямых (рис. 41). 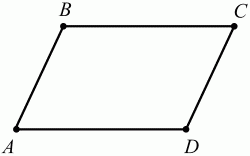 Рис. 41. ABCD – параллелограмм, т. к. ВС||AD и АВ||CD. Прямоугольник – это параллелограмм, у которого все углы прямые (рис. 42). 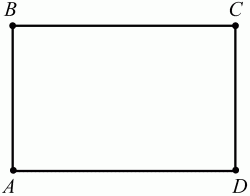 Рис. 42. ABCD – прямоугольник, т. к. ?А = ?В = ?С = ?D = 90°. Ромб – это параллелограмм, у которого все стороны равны (рис. 43). 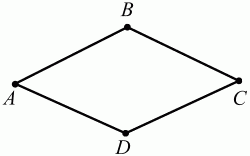 Рис. 43. ABCD – ромб, т. к. AD||ВС и АВ||DC и AB = BC = CD = AD. Квадрат – это прямоугольник, у которого все стороны равны. Можно также сказать, что квадрат – это ромб, у которого все углы прямые (рис. 44). 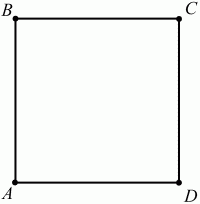 Рис. 44. ABCD – квадрат, т. к. ?А = ?В = ?С = ?D = 90° и АВ = ВС = CD = DA. Трапецией называется четырёхугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами (рис. 45). 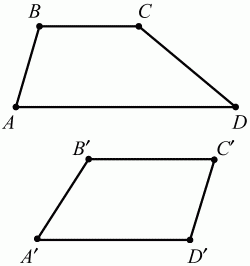 Рис. 45. ABCD и А' В' С' D' – трапеции, т. к. BC||AD, BC||AD. Трапеция, у которой боковые стороны равны, называется раенобокой (рис. 46). 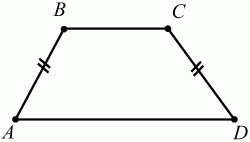 Рис. 46. ABCD – равнобедренная трапеция (АВ = CD). Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции (рис. 47). 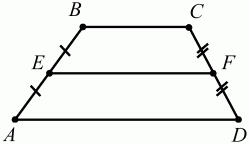 Рис. 47. EF – средняя линия трапеции ABCD: AE = EB, DF = FC. Пусть ВА – перпендикуляр, опущенный из точки В на прямую а, и С – любая точка прямой а, отличная от А. Отрезок ВС называется наклонной, проведённой из точки В к прямой а. Точка С называется основанием наклонной. Отрезок АС называется проекцией наклонной (рис. 48). 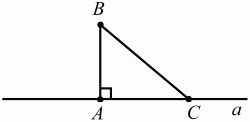 Рис. 48. ВА – перпендикуляр к прямой а, ВС – наклонная. Проведём на плоскости через точку О две взаимно перпендикулярные прямые х и у – оси координат. Ось х (она обычно горизонтальная) называется осью абсцисс, а ось у – осью ординат. Точкой пересечения О – началом координат – каждая из осей разбивается на две полуоси. Условимся одну из полуосей каждой оси называть положительной, отмечая её стрелкой, а другую – отрицательной. Каждой точке А плоскости мы сопоставим пару чисел – координаты точки – абсциссу х и ординату у по следующему правилу. Через точку А проведём прямую, параллельную оси ординат. Она пересечёт ось абсцисс х в некоторой точке Аx. Абсциссой точки А мы будем называть число х, абсолютная величина которого равна расстоянию от точки О до точки Аx. Это число будет положительным, если Аx принадлежит положительной полуоси и отрицательным, если А принадлежит отрицательной полуоси. Если точка А лежит на оси ординат y, то полагаем х равным нулю. Ордината j точки А определяется аналогично. Через точку А проведём прямую, параллельную оси абсцисс х. Она пересечёт ось ординату в некоторой точке Аy. Ординатой точки А мы будем называть число у, абсолютная величина которого равна расстоянию от точки О до точки Аy. Это число будет положительным, если Аy принадлежит положительной полуоси, и отрицательным, если А принадлежит отрицательной полуоси. Если точка А лежит на оси абсцисс х, то полагаем у равным нулю. Координаты точки записывают в скобках рядом с буквенным обозначением точки, например: А(х; у) (на первом месте абсцисса, на втором – ордината) (рис. 49). 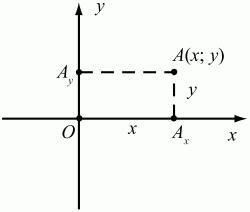 Рис. 49. Уравнением фигуры в декартовых координатах на плоскости называется уравнение с двумя неизвестными х и у, которому удовлетворяют координаты любой точки фигуры. Например, уравнение прямой у = kx + b, где k – тангенс угла наклона прямой к оси Ох (рис. 50). 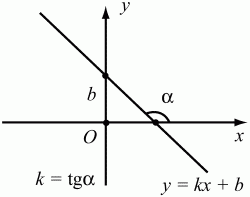 Рис. 50. Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной. Симметрия относительно точки, симметрия относительно прямой, поворот, параллельный перенос – виды движений. Два отрезка называют одинаково направленными, или сонаправленными, если они совмещаются параллельным переносом. Векторы АВ и CD называют одинаково направленными, если отрезки АВ и CD одинаково направлены. Векторы АВ и CD называют противоположно направленными, если отрезки АВ и CD противоположно направлены. Первая буква в обозначении вектора является его началом, а вторая буква – его концом. Например, у вектора АВ точка А – начало вектора, а точка В – его конец (рис. 51). 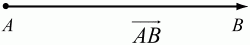 Рис. 51. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Обозначают модуль вектора (на пример, АВ) следующим образом:|АВ|. Очевидно, что |AB| = AB, где АВ – это длина отрезка АВ. Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора (рис. 52). 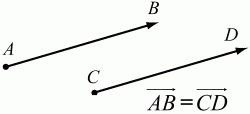 Рис. 52. Пусть вектор а имеет началом точку А1(х1; у1), а концом точку А2(х2; у2). Координатами вектора а будем называть числа a1 = x2 – x1, a2 = y2 – y1. Суммой векторов а и b с координатами а1, а2 и BL, b2 называется вектор с с координатами a1 + BL, a2 + b2. Разностью векторов а (a1; a2) и b (BL; b2) называется такой вектор с (с1; с2), который в сумме с вектором b даёт вектор а, т. е. b + с = а. Отсюда находим координаты вектора с = а – b: с1 = а1 – BL: с2 = а2 – b2. Удобно производить разложение вектора по двум перпендикулярным осям. В этом случае составляющие вектора называются проекциями вектора на оси. Произведением вектора а (a1; a2) на число k называется вектор с координатами (kа1; kа2). Два вектора а и b называются коллинеарными (параллельными), если существует такое число k ? 0, что вектор а есть kb. Разложить вектор а по векторам b и с – значит найти такие числа n, m, что а = nb + mc. Скалярным произведением векторов а (a1; a2) и b (BL; b2) называют число a1BL + a2b2. Углом между ненулевыми векторами АВ и АС называется угол ВАС. Углом между любыми двумя ненулевыми векторами а и b называется угол между равными им векторами с общим началом. Угол между одинаково направленными векторами считается равным нулю. Если векторы перпендикулярны, то их скалярное произведение равно нулю. И обратно: если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны. Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления положительных координатных полуосей, называют координатными векторами или ортами. Преобразование фигуры F в фигуру F1 называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз. Это значит, что если произвольные точки X, Y фигуры F при преобразовании подобия переходят в точки X1, Y1 фигуры F1, то X1Y1 = k ? ХУ, причём число k – одно и то же для всех точек X, Y. Число k называется коэффициентом подобия. При k = 1 преобразование подобия, очевидно, является движением. Пусть F – данная фигура и О – фиксированная точка. Проведём через произвольную точку X фигуры F отрезок ОХ и отложим на нём отрезок ОХ1 равный k ? ОХ, где k – положительное число. Преобразование фигуры F, при котором каждая её точка X переходит в точку X1 построенную указанным способом, называется гомотетией относительно центра О. Число k называется коэффициентом гомотетии, фигуры F и F1 называют гомотетичными. На рис. 53 ?АВС и ?A1В1С1 – гомотетичны. 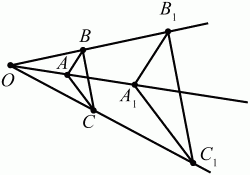 Рис. 53. Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия. Угол разбивает плоскость на две части. Каждая из частей называется плоским углом. Плоские углы с общими сторонами называются дополнительными. Центральным углом в окружности называется плоский угол с вершиной в её центре. Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу. Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла (рис. 54). ?АОВ (угол ?) – центральный. 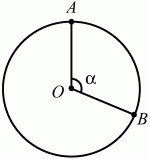 Рис. 54. Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность (рис. 55). 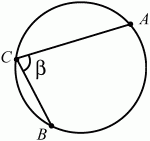 Рис. 55. ?АСВ (угол ?) – вписанный. Геометрическую фигуру будем называть простой, если её можно разбить на конечное число плоских треугольников. Напомним, что плоским треугольником мы называем конечную часть плоскости, ограниченную треугольником. Дадим определение площади для простых фигур. Для простых фигур площадь – это положительная величина, численное значение которой обладает следующими свойствами: 1. Равные фигуры имеют равные площади. 2. Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей. 3. Площадь квадрата со стороной, равной единице, равна единице. 2.2. Вопросы для самопроверки 1. Как принято обозначать точки и прямые на чертеже или в тексте? (1) 2. Что такое отрезок? Нарисуйте произвольный отрезок и отметьте его концы. Как принято обозначать отрезок? (1) 3. Что такое полуплоскость? (1) 4. Что такое луч? Как принято обозначать луч? (1) 5. Какие лучи называются дополнительными? (1) 6. Что такое угол? Как принято обозначать угол? Нарисуйте произвольный угол и укажите его вершину и стороны. (1) 7. Какой угол называется развёрнутым? (1) 8. Как Вы понимаете фразу: «Луч проходит между сторонами данного угла»? (1) 9. В чём измеряют углы? Каковы градусная и радианная мера развёрнутого угла? (1) 10. Какие углы называют смежными? Чему равна сумма смежных углов? (1) 11. Какой угол называется: а) прямым; б) острым; в) тупым? (1) 12. Какие углы называются вертикальными? (1) 13. Какие прямые называются перпендикулярными? Как обозначается перпендикулярность прямых? (1) 14. Что называют перпендикуляром к прямой? Сделайте соответствующий рисунок и покажите основание перпендикуляра. (1) 15. Дайте определение биссектрисы угла. (1) 16. Какая прямая называется секущей по отношению к двум другим? (1) 17. Нарисуйте две прямые и третью – секущую по отношению к первым двум. Покажите на рисунке пары: а) внутренних односторонних; б) внутренних накрест лежащих; в) соответственных углов. (1) 18. Какие прямые называются параллельными? Как обозначается параллельность прямых? (1) 19. Что такое треугольник? Нарисуйте произвольный треугольник и укажите его вершины, стороны и углы. (1) 20. Какие фигуры называются равными? (1) 21. Какой треугольник называется равнобедренным? Нарисуйте равнобедренный треугольник, укажите его основание и боковые стороны. (1) 22. Какой треугольник называется равносторонним? (1) 23. Что такое высота треугольника? Нарисуйте прямоугольный и тупоугольный треугольники и проведите «на глазок» в каждом из них все высоты. (1) 24. Что такое биссектриса треугольника? (1) 25. Что такое медиана треугольника? (1) 26. Что такое внешний угол треугольника? (1) 27. Какой треугольник называется: а) прямоугольным; б) остроугольным; в) тупоугольным? (1) 28. Что такое гипотенуза и катет? (1) 29. Что называют средней линией треугольника? (1) 30. Какой треугольник называется египетским? Приведите пример такого треугольника. (1) 31. Что такое окружность? (1) 32. Что такое круг? (1) 33. Что такое радиус окружности (круга)? (1) 34. Что такое хорда? (1) 35. Что такое дуга окружности? (1) 36. Что такое диаметр окружности (круга)? (1) 37. Что такое сектор круга? (1) 38. Что такое сегмент круга? (1) 39. Что такое серединный перпендикуляр к отрезку? (1) 40. Какая окружность называется описанной около треугольника? (1) 41. Какая окружность называется вписанной в треугольник? (1) 42. Что такое касательная к окружности? (1) 43. Как вы понимаете высказывания: «внутреннее касание окружностей», «внешнее касание окружностей»? (1) 44. Что такое общая касательная к окружностям? (1) 45. В каких случаях две окружности имеют: а) одну; б) две; в) три; r) четыре общих касательных? (2) 46. Что означает решить задачу на построение с помощью циркуля и линейки? (1) 47. Какой смысл вкладывается в следующие этапы решения задач на построение: анализ, построение, доказательство, исследование? (2) 48. Как вы понимаете термин «геометрическое место точек»? (1) 49. В чём состоит сущность метода геометрических мест, используемого при решении задач на построение? (2) 50. Что такое ломаная? (1) 51. Какая ломаная называется замкнутой? (1) 52. Дайте определение многоугольника (на плоскости). Нарисуйте произвольный пятиугольник, отметьте его вершины и проведите в нём все диагонали. (1) 53. Какой многоугольник называется выпуклым? (1) 54. Какой многоугольник называется правильным? (1) 55. Какой многоугольник называется: вписанным в окружность; описанным около окружности? (1) 56. Что называют периметром многоугольника? (1) 57. Дайте определение параллелограмма. (1) 58. Дайте определение прямоугольника. (1) 59. Дайте определение ромба. (1) 60. Дайте различные определения квадрата. (1) 61. Дайте определение трапеции. Какие стороны трапеции называются основаниями, какие – боковыми сторонами? (1) 62. Какая трапеция называется равнобокой? (1) 63. Что называют средней линией трапеции? (1) 64. Что называют наклонной, проведённой из точки, не лежащей на прямой, на эту прямую? Что называют проекцией этой наклонной? (1) 65. Как на плоскости вводится декартова система координат? (1) 66. Что такое абсцисса и ордината точки? (1) 67. Что называют уравнением фигуры? (1) 68. Какой геометрический смысл имеет число k в уравнении прямой у = kx + в?(1) 69. Что такое движение? (1) 70. Назовите виды движений на плоскости. Покажите на конкретных примерах, как построить образы фигур при данных видах движений. (1) 71. Какие два луча называются сонаправленными и противоположно направленными? (1) 72. Что такое вектор? Как обозначать вектор? (1) 73. Какие два вектора называются одинаково направленными и противоположно направленными? (1) 74. Что такое абсолютная величина (модуль) вектора? (1) 75. Какой вектор называют нулевым? (1) 76. Какие два вектора назьшают равными? (1) 77. Как вводятся координаты вектора через координаты его начала и конца? (1) 78. Что называют суммой векторов? Нарисуйте два произвольных вектора и покажите их сумму. (1) 79. Что назьшают разностью векторов? Нарисуйте два произвольных вектора и покажите их разность. (1) 80. Что называют проекцией вектора на ось? Покажите на рисунке. (1) 81. Что называют произведением вектора на число? Нарисуйте произвольный вектор а, а также b = 2а и с = -1/2а (1) 82. Что значит разложить вектор а по векторам b и с? (1) 83. Дайте определение скалярного произведения векторов. (1) 84. Что называют углом между векторами? Чем отличается угол между векторами от угла между прямыми? (1) 85. В каком случае скалярное произведение векторов равно нулю? (1) 86. Дайте определение координатного вектора (орта). (1) 87. Какое преобразование называется преобразованием подобия? (1) 88. Что такое гомотетия? (1) 89. Какие фигуры называются подобными? Как обозначать подобие фигур? (1) 90. Что называют центральным углом в окружности? (1) 91. Как определить градусную меру дуги окружности? (1) 92. Какой угол называется вписанным в окружность? (1) 93. Как в курсе геометрии вводится понятие площади? (2) 2.3. Темы для сообщений и рефератов 1. Замечательные точки в треугольнике. (1) 2. Вневписанные окружности. (1–2) 3. Радикальная ось и радикальный центр окружностей. Пучки окружностей. (3) 4. Полярное соответствие. Принцип двойственности в геометрии. (3) 5. Отображения и преобразования множеств. Композиция преобразований. Аффинные преобразования плоскости. (3) 6. Инверсия плоскости относительно окружности. (3) 7. Понятие длины. Расстояние между фигурами. (2) § 3. Важнейшие теоремы и формулы школьного курса планиметрии 3.1. Справочная информация Приведём без доказательства основные теоремы планиметрии. Доказательства желательно изучать по вашему учебнику. Опасно изучать доказательство теорем по разным учебным пособиям – можно в погоне за простотой попасться на капкане «порочного круга». Приведём простой пример. Нужно доказать признаки параллельных прямых (если при пересечении двух прямых третьей сумма образовавшихся внутренних односторонних углов равна 180°, то прямые параллельны). На рис. 56:m, n, a – прямые. Точка А – точка пересечения прямых m и а, В – точка пересечения прямых n и а. 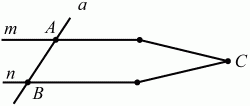 Рис. 56. Ученик привёл простое доказательство: если бы прямые m и n пересекались в некоторой точке С, то тогда из того, что сумма углов в треугольнике АСВ равна 180°, следует, что ?АСВ = 0°, что невозможно. Значит, прямые m и n параллельны. Но тут же ученику предложили доказать, что сумма углов в треугольнике равна 180°. Учащийся сослался на свойства параллельных прямых. Но сами свойства параллельных прямых он стал доказывать на основе признаков параллельности прямых. Круг замкнулся. Поэтому в повторении теории будьте последовательны и внимательны. При чтении доказательства теоремы особое внимание обращайте на то, где в доказательстве использованы условия теоремы, какие ранее доказанные теоремы при этом использовались. В настоящем параграфе формулировки теорем приведены по учебнику А. В. Погорелова «Геометрия. 7–9 классы». Основные теоремы планиметрии и следствия из них1. Теоремы о прямых (параллельность и перпендикулярность на плоскости)Свойства параллельных прямых. Две прямые, параллельные третьей, параллельны (рис. 57). (а||с, b||с) ? а||b.  Рис. 57. Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180° (рис. 58). а||b ? ? = ? ? + ? = 180°. 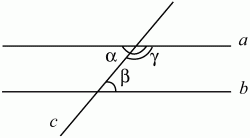 Рис. 58. Признаки параллельности прямых. Если при пересечении двух прямых третьей образующиеся внутренние накрест лежащие углы равны, то прямые параллельны (рис. 59): внутренние накрест лежащие углы равны ? а||b. 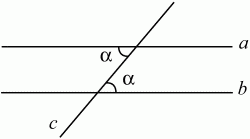 Рис. 59. Если при пересечении двух прямых третьей сумма образовавшихся внутренних односторонних углов равна 180°, то прямые параллельны (рис. 60): а||b. 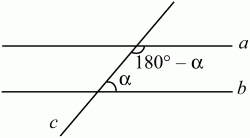 Рис. 60. Если при пересечении двух прямых третьей образующиеся соответственные углы равны, то прямые параллельны (рис. 61): а||b. 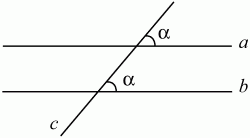 Рис. 61. Теоремы о существовании и единственности перпендикуляра к прямой. Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну (рис. 62). 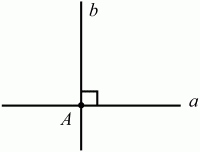 Рис. 62. Прямая b – единственная прямая, проходящая через точку А перпендикулярно а. Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один (рис. 63). 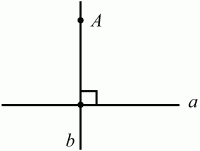 Рис. 63. Прямая b – единственная прямая, проходящая через точку А перпендикулярно а. Связь между параллельностью и перпендикулярностью. Две прямые, перпендикулярные третьей, параллельны (рис. 64). (а ? с, b ? с) ? а||b. 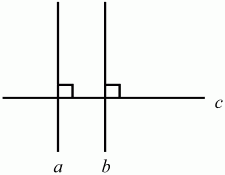 Рис. 64. Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой (рис. 65): (а ? b, b||с) ? а ? с. 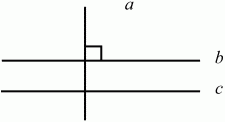 Рис. 65. 2 Теоремы об углах. Углы в треугольнике. Вписанные в окружность углыСвойство вертикальных углов. Вертикальные углы равны (рис. 66): ? = ?. 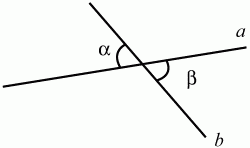 Рис. 66. Свойство углов равнобедренного треугольника. В равнобедренном треугольнике углы при основании равны. Верна и обратная теорема: если в треугольнике два угла равны, то он равнобедренный (рис. 67): АВ = ВС ? ?А = ?С. 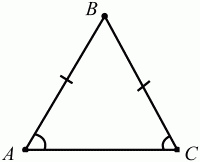 Рис. 67. Теорема о сумме углов в треугольнике. Сумма внутренних углов треугольника равна 180° (рис. 68): ? + ? + ? = 180°. 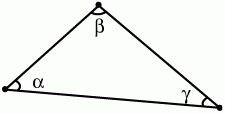 Рис. 68. Теорема о сумме углов в выпуклом n-угольнике. Сумма углов выпуклого n-угольника равна 180°?(n – 2) (рис. 69). 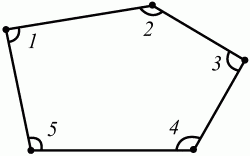 Рис. 69. Пример:?1 + ?2 + ?3 + ?4 + ?5 = 180°?(5–2) = 540°. Теорема о внешнем угле треугольника. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним (рис. 70): ? = ? + ?. 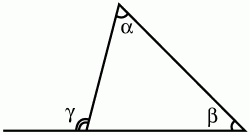 Рис. 70. Теорема о величине вписанного в окружность угла. Угол, вписанный в окружность, равен половине соответствующего q центрального угла (рис. 71): 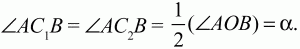 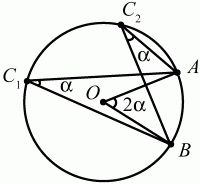 Рис. 71. 3. Основные теоремы о треугольникеПризнаки равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 72). 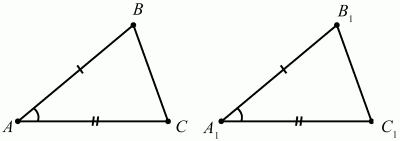 Рис. 72. ?ABC = ?A1B1C1 т. к. АB = А1В1, АС = А1С1 и ?A = ?A1. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 73). 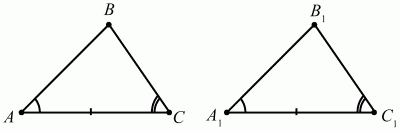 Рис. 73. ?ABC = ?A1B1C1 т. к. АC = А1C1, ?A = ?A1, ?C = ?C1. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны (рис. 74). 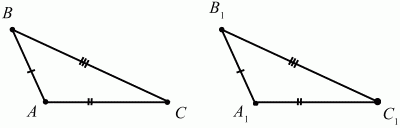 Рис. 74. ?ABC = ?A1B1C1 т. к. АB = А1B1, АC = А1C1, BC = B1C1. Признаки равенства прямоугольных треугольников. Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны (рис. 75). 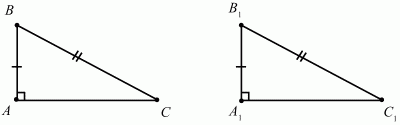 Рис. 75. ?ABC = ?A1B1C1 т. к. ?А = ?А1 = 90°; BC = B1C1; AB = A1B1. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны (рис. 76). 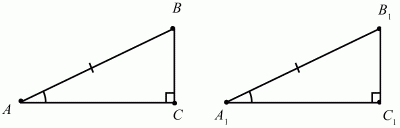 Рис. 76. ?АВС = ?А1В1С1, т. к. АВ = А1В1, ?А = ?A1 a ?С = ?С1 = 90°. Свойство медианы равнобедренного треугольника. В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой (рис. 77). 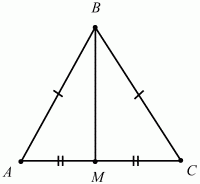 Рис. 77. (АВ = ВС, АМ = МС) ? (?АВМ = ?МВС, ?АМВ = ?ВМС = 90°). Свойство средней линии треугольника. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине (рис. 78). 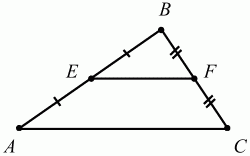 Рис. 78. EF||AC, EF = 1/2АС, т. к. АЕ = ЕВ и BF = FC. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов (рис. 79). 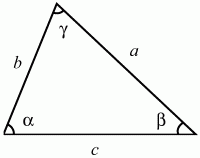 Рис. 79. 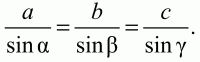 Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними (рис. 80). 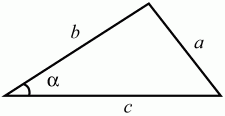 Рис. 80. а2= b2+ с2– 2bc cos ?. Теорема Пифагора (частный случай теоремы косинусов). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (рис. 81). 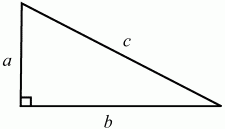 Рис. 81. с2= а2+ b2. 4. Пропорциональность и подобие на плоскостиТеорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне (рис. 82). 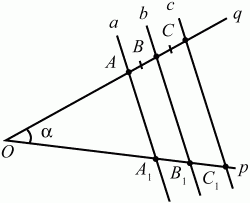 Рис. 82. (АВ = BC, AA1||BB1||CC1) ? A1B1 = В1С1, q и р – лучи, образующие угол ?. а, b, с – прямые, пересекающие стороны угла. Теорема о пропорциональных отрезках (обобщение теоремы Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки (рис. 83). 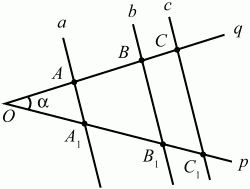 Рис. 83. 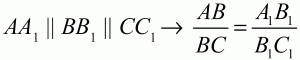 или 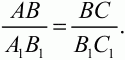 Свойство биссектрисы треугольника. Биссектриса угла треугольника делит противолежащую ему сторону на отрезки, пропорциональные двум другим сторонам (рис. 84). 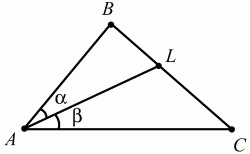 Рис. 84. Если ? = ?, то 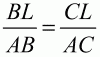 или 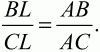 Признаки подобия треугольников. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны (рис. 85). 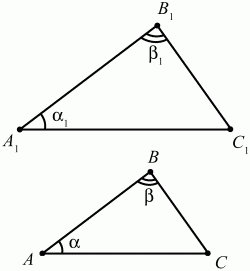 Рис. 85. Треугольники ABC и A1B1C1 – подобные, т. к. ? = ?1 и ? = ?1. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то треугольники подобны (рис. 86). 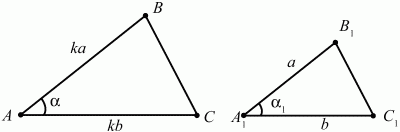 Рис. 86. Треугольники ABC и A1B1C1 – подобны, т. к. 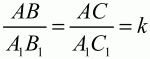 и ? = ?1. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны (рис. 87). 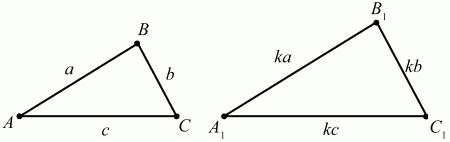 Рис. 87. Треугольники ABC и A1B1C1 – подобны, т. к 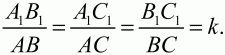 5. Основные геометрические неравенства 5. Основные геометрические неравенстваСоотношение длин наклонной и перпендикуляра. Если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше (рис. 88): АА' < АВ < АС; если А'С > А'В, то АС > АВ. 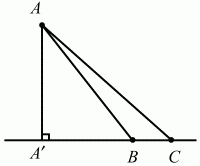 Рис. 88. Неравенство треугольника. Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки. Отсюда следует, что в любом треугольнике каждая сторона меньше суммы двух других сторон (рис. 89): АС < АВ + ВС. 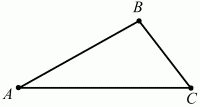 Рис. 89. Связь между величинами сторон и величинами углов в треугольнике. В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол (рис. 90). (BC < AB < AC) ? (?А < ?С < ?В). 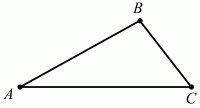 Рис. 90. 6. Основные геометрические места точек на плоскостиГеометрическим местом точек плоскости, равноудалённых от сторон угла, будет биссектриса данного угла (рис. 91). 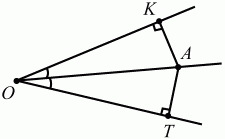 Рис. 91. АК = AT, где А – любая точка на биссектрисе. Геометрическим местом точек, равноудалённых от двух данных точек, будет прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину (рис. 92). 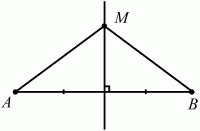 Рис. 92. MA = MB, где М – произвольная точка на серединном перпендикуляре отрезка АВ. Геометрическим местом точек плоскости, равноудалённых от заданной точки, будет окружность с центром в этой точке (рис. 93).  Рис. 93. Точка О равноудалена от точек окружности. Местоположение центра окружности, описанной около треугольника. Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведённых через середины этих сторон (рис. 94). 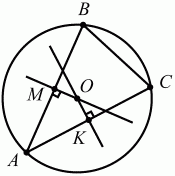 Рис. 94. А, В, С – вершины треугольника, лежащие на окружности. АМ = МВ и АК = КС. Точки М и К – основания перпендикуляров к сторонам АВ и АС соответственно. Местоположение центра окружности, вписанной в треугольник. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис (рис. 95). 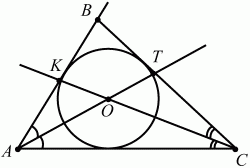 Рис. 95. В ?ABC отрезки AT и СК являются биссектрисами. 7. Теоремы о четырёхугольникахСвойства параллелограмма. У параллелограмма противолежащие стороны равны. У параллелограмма противолежащие углы равны. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам (рис. 96). 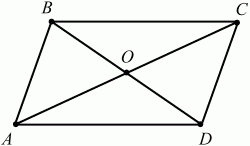 Рис. 96. АВ = CD, ВС = AD, ?BAD = ?BCD, ?АВС = ?ADC, AO = OC, BO = OD. Признаки параллелограмма. Если у четырёхугольника две стороны параллельны и равны, то он является параллелограммом (рис. 97). 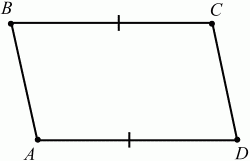 Рис. 97. ВС||AD, ВС = AD ? ABCD – параллелограмм. Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм (рис. 98). 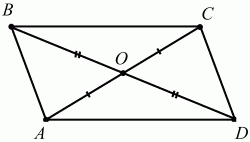 Рис. 98. АО = ОС, ВО = OD ? ABCD – параллелограмм. Свойства прямоугольника. Для прямоугольника характерны все свойства параллелограмма (у прямоугольника противолежащие стороны равны; у прямоугольника противолежащие углы равны (90°); диагонали прямоугольника пересекаются и точкой пересечения делятся пополам). Диагонали прямоугольника равны (рис. 99): АС = BD. 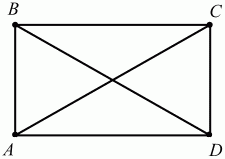 Рис. 99. Признак прямоугольника. Если у параллелограмма все углы равны, то он является прямоугольником. Свойства ромба. Для ромба характерны все свойства параллелограмма (у ромба противолежащие стороны равны – вообще все стороны по определению равны; у ромба противолежащие углы равны; диагонали ромба пересекаются и точкой пересечения делятся пополам). Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисами его углов (рис. 100). 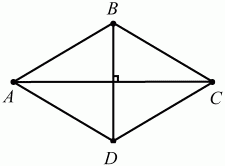 Рис. 100. AC ? BD, ?ABD = ?DВС = ?CDB = ?BDA, ?ВАС = ?CAD = ?ВСА = ?DCA. Признак ромба. Если у параллелограмма диагонали перпендикулярны, то он является ромбом. Свойства квадрата. Квадрат обладает свойствами прямоугольника и ромба. Признак квадрата. Если диагонали прямоугольника пересекаются под прямым углом, то он – квадрат. Свойство средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме (рис. 101). 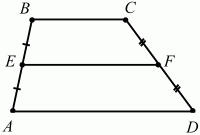 Рис. 101. 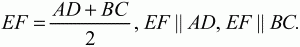 Критерии вписанного и описанного четырехугольников. Если около четырёхугольника можно описать окружность, то суммы его противоположных углов равны по 180° (рис. 102). ?А + ?С = ?В + ?D = 180°. 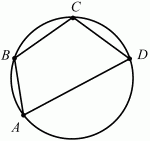 Рис. 102. Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны (рис. 103). AB + CD = AD + BC. 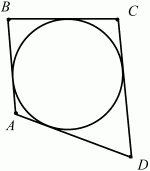 Рис. 103. 8. Теоремы об окружностяхСвойство хорд и секущих. Если хорды АВ и CD окружности пересекаются в точке S, то AS ? BS = CS ? DS (рис. 104). 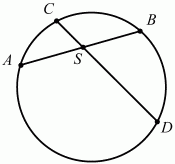 Рис. 104. Если из точки S к окружности проведены две секущие, пересекающие окружность в точках А, В и С, D соответственно, то AS ? BS = CS ? DS (рис. 105). 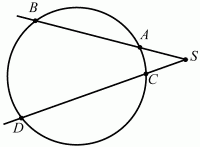 Рис. 105. Число ?. Отношение длины окружности к её диаметру не зависит от радиуса окружности, то есть оно одно и то же для любых двух окружностей. Это число равно ? (рис. 106). 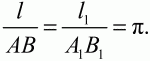 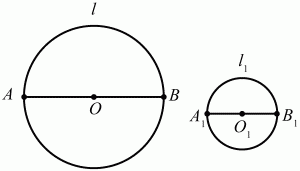 Рис. 106. 9. ВекторыТеорема о разложении вектора по базису. Если на плоскости даны два неколлинеарных вектора а и b и любой другой вектор с, то существуют единственные числа n и m, такие, что с = nа + mb (рис. 107). где 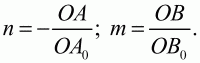 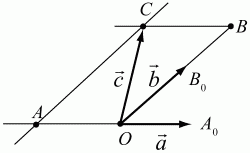 Рис. 107. Теорема о скалярном произведении векторов. Скалярное произведение векторов равно произведению их абсолютных q величин (длин) на косинус угла между ними (рис. 108). ОА ? ОВ = ОА ? OB ? cos ?. 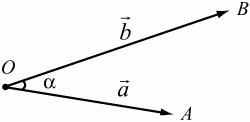 Рис. 108. Основные формулы планиметрииДля треугольника (рис. 109): 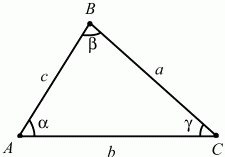 Рис. 109. 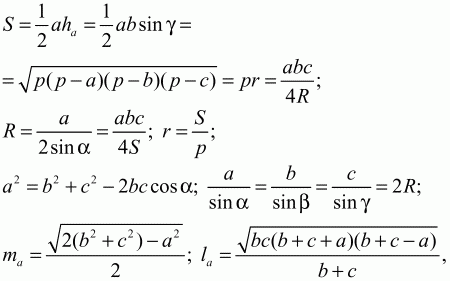 где a, b, с – стороны треугольника; ?, ?, ? – противолежащие им углы; r и R – радиусы вписанной и описанной окружностей; ha, ma, la – высота, медиана и биссектриса, проведённые к стороне а; S – площадь треугольника; 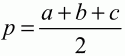 – полупериметр треугольника. Медианы в треугольнике делятся точкой пересечения в отношении 2:1, считая от вершины (рис. 110). 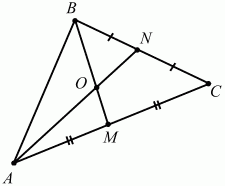 Рис. 110. 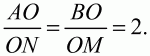 Для четырёхугольников: 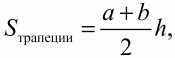 где а, b – длины оснований; h – высота трапеции. Площадь параллелограмма со сторонами а, b и углом ? между ними вычисляется по формуле S = ab sin ?. Можно также воспользоваться формулой: 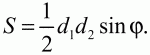 где d1, d2– длины диагоналей, ? – угол между ними (или S = aha, где ha – высота). Для произвольного выпуклого четырёхугольника (рис. 111): 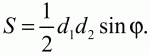 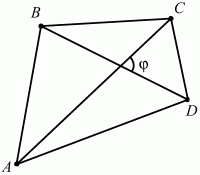 Рис. 111. Для правильного n-угольника: 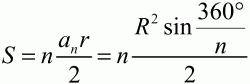 (R и r – радиусы описанной и вписанной окружностей, аn – длина стороны правильного n-угольника). Для окружности и круга (рис. 112): 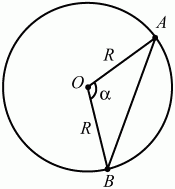 Рис. 112. 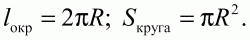 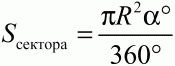 и 1\2R2?, если ? выражен в радианах. Sсегмента = Sсектора – Sтреугольника. Формулы аналитической планиметрииЕсли даны точки A(x1; y1) и В(х2; у2), то 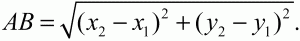 Уравнение прямой АВ: 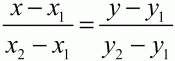 легко приводится к виду ах + by + с = 0, где вектор n = (а, b) перпендикулярен прямой. Расстояние от точки А(х1; у1) до прямой ах + by + с = 0 равно 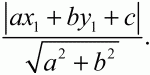 Расстояние между параллельными прямыми ах + by + с1 = 0 и ах + by + с2 = 0 равно 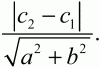 Угол между прямыми а1х + BLу + с1 = 0 и а2х + b2y + с2 = 0 вычисляется по формуле: 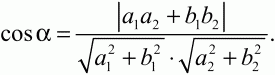 Уравнение окружности с центром в точке O(x0, y0) и радиусом R:(x – xo)2+ (y – yo)2= R2. 3.2. Вопросы для самопроверки 1. а) Какое вы знаете свойство вертикальных углов? (1) б) Докажите это свойство. (1) 2. а) Сформулируйте признак равенства треугольников по двум сторонам и углу между ними. (1) б) Докажите данный признак. (1) 3. а) Сформулируйте признак равенства треугольников по стороне и двум углам. (1) б) Докажите данный признак. (1) 4. а) Перечислите основные свойства равнобедренного треугольника. (1) б) Докажите эти свойства. (1) в) Докажите признак равнобедренного треугольника. (1) 5. а) Сформулируйте признак равенства треугольников по трём сторонам. (1) б) Докажите данный признак. (1) 6. Докажите, что две прямые, параллельные третьей, параллельны. (2) 7. а) Сформулируйте признаки параллельности прямых. (1) б) Докажите эти признаки. (1) в) Докажите обратные теоремы. (1) 8. Докажите теорему о сумме углов треугольника. (1) 9. Докажите, что внешний угол треугольника равен сумме двух внутренних, не смежных с ним. (1) 10. а) Сформулируйте признаки равенства прямоугольных треугольников. (1) б) Докажите признаки равенства прямоугольных треугольников по гипотенузе и катету; по гипотенузе и острому углу. (1) 11. а) Докажите, что из точки, не лежащей на данной прямой, можно опустить на эту прямую единственный перпендикуляр. (1) б) Докажите, что через точку, лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной. (1) 12. а) Где лежит центр описанной около треугольника окружности? (1) б) Докажите соответствующую теорему. (1) 13. а) Где лежит центр вписанной в треугольник окружности? (1) б) Докажите соответствующую теорему. (1) 14. Докажите свойство касательной к окружности. (1) 15. а) Какие вы знаете свойства параллелограмма? (1) б) Докажите эти свойства. (1) 16. а) Какие вы знаете признаки параллелограмма? (1) б) Докажите эти признаки. (1) 17. а) Какие вы знаете свойства и признаки прямоугольника? (1) б) Докажите эти свойства и признаки. (1) 18. а) Какие вы знаете свойства и признаки ромба? (1) б) Докажите эти свойства и признаки. (1) 19. а) Какие вы знаете свойства и признаки квадрата? (1) б) Докажите эти свойства и признаки. (1) 20. а) Сформулируйте теорему Фалеса. (1) б) Докажите эту теорему. (1) 21. а) Сформулируйте обобщенную теорему Фалеса (теорему о пропорциональных отрезках). (1) б) Докажите эту теорему. (2) 22. а) Какие свойства средней линии треугольника вы знаете? (1) б) Докажите эти свойства. (1) 23. а) Какие вы знаете свойства средней линии трапеции? (1) б) Докажите эти свойства. (1) 24. а) Сформулируйте теорему Пифагора. (1) б) Докажите теорему Пифагора. (1) в) Сформулируйте и докажите обратную теорему. (2) 25. Докажите, что любая наклонная больше перпендикуляра, и что из двух наклонных больше та, у которой больше проекция. (1) 26. а) Сформулируйте неравенство треугольника. (1) б) Докажите неравенство треугольника. (2) 27. Даны координаты точек A(х1; у1) и В(х2; у2). а) По какой формуле вычисляется длина отрезка AB? (1) б) Выведите эту формулу. (1) 28. Выведите уравнение окружности с центром в точке А(х0; у0) и радиусом R. (1) 29. Докажите, что любая прямая в декартовых координатах х, у имеет уравнение вида ах + by + с = 0. (2) 30. Напишите уравнение прямой, проходящей через точки А(х1; у1) и В(х2; у2). Ответ: обоснуйте. (2) 31. Докажите, что в уравнении прямой у = kx + b число k есть тангенс угла наклона прямой к положительному направлению оси абсцисс. (2) 32. а) Какие вы знаете основные свойства движений? (2) б) Докажите эти свойства. (3) 33. Докажите, что: а) преобразование симметрии относительно точки является движением; (3) б) преобразование симметрии относительно прямой является движением; (3) в) параллельный перенос есть движение. (3) 34. Докажите теорему о существовании и единственности параллельного переноса. (3) 35. Докажите, что абсолютная величина вектора kа равна |к| ? |а|, при этом направление вектора kа при а ? О совпадает с направлением вектора а, если k > 0, и противоположно направлению вектора а, если к < 0. (1) 36. Докажите, что любой вектор а можно разложить по векторам b и с (все три вектора лежат на одной плоскости). (1) 37. Даны векторы а = (а1; а2) и b = (BL; b2). Докажите, что 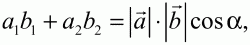 где ? – угол между векторами. 38. а) Какие вы знаете свойства скалярного произведения векторов? (1) б) Докажите эти свойства. (2) 39. Докажите, что гомотетия есть преобразование подобия. (1) 40. а) Какие вы знаете свойства преобразования подобия? (1) б) Докажите, что преобразование подобия сохраняет углы между лучами. (2) 41. а) Сформулируйте признак подобия треугольников по двум углам. (1) б) Докажите этот признак. (1) 42. а) Сформулируйте признак подобия треугольников по двум сторонам и углу между ними. (1) б) Докажите этот признак. (1) 43. а) Сформулируйте признак подобия треугольников по трём сторонам. (1) б) Докажите этот признак. (2) 44. а) Сформулируйте свойство биссектрисы треугольника. (1) б) Докажите, что биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам. (1) 45. а) Сформулируйте свойство вписанного в окружность угла. (1) б) Докажите это свойство. (1) 46. а) Докажите, что если хорды АВ и CD окружности пересекаются в точке S, то AS ? BS = CS ? DS. (1) б) Докажите, что если из точки S к окружности проведены две секущие, пересекающие окружность в точках А, В и С, D соответственно, то AS ? BS = CS ? DS. (1) 47. а) Сформулируйте теорему косинусов для треугольника. (1) б) Докажите эту теорему. (1) 48. а) Сформулируйте теорему синусов. (1) б) Докажите эту теорему. (1) в) Докажите, что в теореме синусов каждое из трёх отношений: 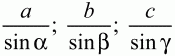 равно 2R, где R – радиус описанной около треугольника окружности. (1) 49. Докажите, что в треугольнике против большей стороны лежит больший угол, а против большего угла лежит большая сторона. (2) 50. а) Чему равна сумма углов выпуклого n-угольника? (1) б) Выведите формулу суммы углов выпуклого n-угольника. (1) 51. а) Докажите, что в правильный многоугольник можно вписать окружность. (1) б) Докажите, что около правильного многоугольника можно описать окружность. (1) 52. Дан правильный n-угольник со стороной а. Выведите формулы: а) радиусов вписанной и описанной окружностей; (1) б) площади n-угольника; (1) в) угла при вершине. (1) 53. Докажите, что отношение длины окружности к её диаметру не зависит от размера окружности. (3) 54. Как переводить углы из градусной меры в радианную и наоборот? (1) 55. Докажите, что площадь прямоугольника равна произведению длины прямоугольника на его ширину. (3) 56. а) По какой формуле вычисляется площадь параллелограмма? (1) б) Выведите эту формулу. (1) 57. а) По какой формуле вычисляется площадь треугольника? (через основание и высоту). (1) б) Выведите эту формулу. (1) в) Выведите формулу Герона. (1) 58. а) По какой формуле вычисляется площадь трапеции? (1) б) Выведите эту формулу. (1) 59. Выведите формулы: 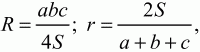 где a, b, c – длины сторон треугольника; S – его площадь; R и r – радиусы описанной и вписанной окружностей. (1) 60. Пусть F1 и F2 – две подобные фигуры с коэффициентом подобия k. Как относятся площади этих фигур? Ответ: обоснуйте. (1) 61. а) По какой формуле вычисляется площадь круга? (1) б) Выведите эту формулу. (3) 62. Выведите формулу площади кругового сектора. (2) 63. Выведите формулу площади кругового сегмента. (2) 64. а) Докажите, что биссектрисы треугольника пересекаются в одной точке. (2) б) Докажите, что медианы треугольника пересекаются в одной точке. (2) в) Докажите, что высоты треугольника (или их продолжения) пересекаются в одной точке. (2) г) Докажите, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. (1) 65. Докажите, что площадь треугольника равна половине произведения двух его сторон на синус угла между ними. (1) 66. а) Сформулируйте теорему Чевы. (3) б) Докажите эту теорему. (3) в) Сформулируйте и докажите обратную теорему. (3) 67. а) Сформулируйте теорему Мене лая. (3) б) Докажите эту теорему. (3) в) Сформулируйте и докажите обратную теорему. (3) 68. а) Докажите, что если стороны одного угла параллельны сторонам другого угла, то такие углы либо равны, либо составляют 180°. (2) б) Докажите, что если стороны одного угла перпендикулярны сторонам другого угла, то такие углы равны или составляют 180°. (2) 69. Докажите, что медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. (1) 70. Докажите, что площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними. (1) 71. Выведите формулу длины медианы треугольника (через его стороны). (2) 72. Выведите формулу длины биссектрисы треугольника (через его стороны). (2) 73. а) Сформулируйте критерий описанного четырёхугольника. (1) б) Докажите соответствующую теорему. (2) 74. а) Сформулируйте критерий вписанного четырёхугольника. (1) б) Докажите соответствующую теорему. (2) 3.3. Задачи теоретического характера для самостоятельного решения и разбора на факультативных занятиях 1. Докажите, что 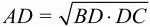 (рис. 113). (1) 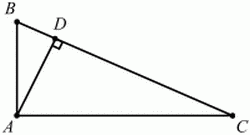 Рис. 113. 2. Докажите, что центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы. (1) 3. Докажите, что сумма внешних А углов выпуклого n-угольника равна 360°. (1) 4. Докажите, что через три точки, не лежащие на одной прямой, можно провести окружность и притом только одну. (1) 5. Около какого параллелограмма можно описать окружность? Ответ: поясните. (1) 6. Во всякий ли параллелограмм можно вписать окружность? Ответ: обоснуйте. (1) 7. Около какой трапеции можно описать окружность? Почему? (1) 8. АВ = а, ВС = b. Найдите длину BD (рис. 114). (1) 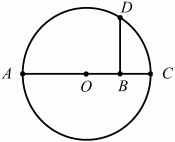 Рис. 114. 9. АС = a, AD = b. Найдите длину АВ (рис. 115). (1) 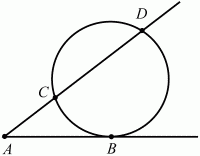 Рис. 115. 10. В каком отношении точка X делит отрезок АВ, если известно, что длина всего отрезка АВ так относится к длине большей части АХ, как большая часть к меньшей части ХВ («золотое сечение») (рис. 116)? (1)  Рис. 116. 11. Могут ли две прямые иметь две точки пересечения? Объясните ответ. (1) 12. Могут ли точки А, В, С лежать на одной прямой, если АВ = 1,8 м, АС = 1,3 м, ВС = 3 м? Объясните ответ. (1) 13. Может ли прямая, пересекающая одну из двух параллельных прямых, не пересекать другую? Объясните ответ. (1) 14. Может ли прямая, не проходящая ни через одну из вершин треугольника, пересекать каждую его сторону? Почему? (1) 15. Найдите угол между биссектрисами смежных углов. (1) 16. Докажите, что биссектрисы вертикальных углов лежат на одной прямой. (1) 17. Докажите, что у равнобедренного треугольника:1) биссектрисы, проведённые из вершин при основании, равны; 2) медианы, проведённые из тех же вершин, тоже равны. (1) 18. Докажите равенство треугольников по углу, биссектрисе этого угла и стороне, прилежащей к этому углу. (1) 19. Даны два равнобедренных треугольника с общим основанием. Докажите, что их медианы, проведённые к основанию, лежат на одной прямой. (1) 20. Докажите равенство треугольников по двум сторонам и медиане, проведённой к одной из них. (1) 21. Докажите, что биссектрисы внутренних накрест лежащих углов, образованных параллельными и секущей, параллельны, т. е. лежат на параллельных прямых. (1) 22. Отрезки АВ и CD пересекаются в точке Е и делятся этой точкой пополам. Докажите, что прямые АС и BD параллельны. (1) 23. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию. (1) 24. В треугольнике ABC медиана BD равна половине стороны АС. Найдите угол В треугольника. (1) 25. Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок её, заключённый между параллельными сторонами, делится этой точкой пополам. (1) 26. Докажите, что если диагонали прямоугольника пересекаются под прямым углом, то он – квадрат. (1) 27. Докажите, что вершины треугольника равноудалены от прямой, проходящей через середины двух его сторон. (1) 28. Докажите, что середины сторон четырёхугольника являются вершинами параллелограмма. (1) 29. Докажите, что середины сторон прямоугольника являются вершинами ромба. И наоборот, середины сторон ромба являются вершинами прямоугольника. (1) 30. Докажите, что у равнобокой трапеции углы при основании равны. (1) 31. Докажите, что любая сторона треугольника больше разности двух других его сторон. (1) 32. Докажите, что медиана треугольника ABC, проведённая из вершины А, меньше полусуммы сторон АВ и АС. (1) 33. Могут ли пересекаться окружности с радиусами R1 и R2 и расстоянием между центрами d, если R1 + R2 < d? (1) 34. Найдите радиус r окружности, вписанной в равносторонний треугольник со стороной а, и радиус R окружности, описанной около него. (1) 35. Найдите геометрическое место точек плоскости ху, для которых |х| = 3. (1) 36. Составьте уравнение окружности с центром в точке (1; 2), касающейся оси х. (1) 37. Докажите, что прямая, содержащая медиану равнобедренного треугольника, проведённую к основанию, является осью симметрии треугольника. (1) 38. Сколько осей симметрии у равностороннего треугольника? (1) 39. Докажите, что ромбы равны, если у них равны диагонали. (1) 40. Даны точки A(0; 1), В(1; 0), С(1; 2), D(2; 1). Докажите равенство векторов АВ и CD.(1) 41. Дан параллелограмм ABCD, AC = a, DB = b. Выразите векторы АВ, СВ, CD и АD через а и b (рис. 117).(1) 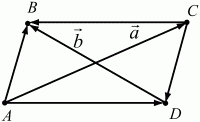 Рис. 117. 42. Докажите, что для любого вектора 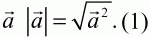 43. Докажите, что дуги окружности, заключённые между параллельными хордами, равны. (2) 44. Докажите правильность соотношения 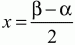 (рис. 118). (2) 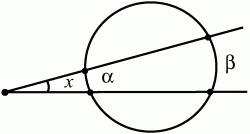 Рис. 118. 45. Докажите правильность соотношения 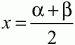 (рис. 119). (2) 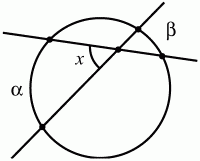 Рис. 119. 46. АВ – касательная. Докажите, что х = ?/2 (рис. 120). (2) 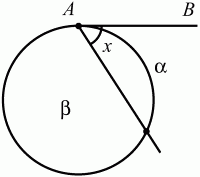 Рис. 120. 47. Докажите, что если два треугольника подобны с коэффициентом подобия k, то с тем же коэффициентом подобия подобны соответствующие линейные элементы этих треугольников (высоты, медианы, радиусы описанной и вписанной окружностей, периметры и т. д.). (2) 48. Докажите, что если для четырёх точек плоскости А, В, М и К выполняется одно из следующих условий: а) точки М и К расположены по одну сторону от прямой АВ и при этом ?АМВ = ?АКБ; б) точки М и К расположены по разные стороны от прямой АВ и при этом ?АМВ + ?АКБ = 180°, то точки А, В, М и К лежат на одной окружности. (2) 49. Докажите, что биссектриса внешнего угла треугольника обладает свойством, аналогичному биссектрисе внутреннего угла, а именно: 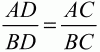 (рис. 121). (2) 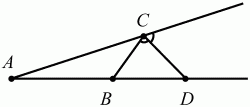 Рис. 121. 50. ABC – произвольный треугольник. СР и AQ – высоты. Докажите, что треугольник ABC и треугольник PBQ подобны. Чему равен коэффициент подобия (рис. 122)? (2) 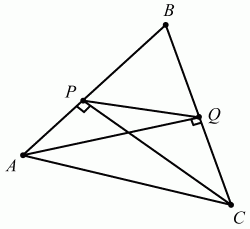 Рис. 122. 51. Докажите равенство треугольников по медиане и углам, на которые медиана разбивает угол треугольника. (2) 52. Докажите равенство треугольников по стороне, медиане, проведённой к этой стороне, и углам, которые образует с ней медиана. (2) 53. Разделите отрезок АВ с помощью циркуля и линейки на n равных частей. (2) 54. На стороне АВ треугольника ABC взята точка X Докажите, что отрезок СХ меньше, по крайней мере, одной из сторон АС или ВС. (2) 55. Какая геометрическая фигура задана уравнением 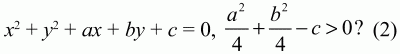 56. Докажите, что при движении параллелограмм переходит в параллелограмм. (2) 57. Докажите, что у параллелограмма точка пересечения диагоналей является центром симметрии. (2) 58. Докажите, что отрезки, соединяющие противоположные вершины описанного шестиугольника, пересекаются в одной точке (теорема Брианшона). (3) 59. Докажите, что основания перпендикуляров, проведённых к прямым, содержащим стороны треугольника, из произвольной точки описанной около него окружности, лежат на одной прямой (теорема Симпсона). (3) 60. Докажите, что если противоположные стороны вписанного шестиугольника не параллельны, то точки пересечения продолжений этих сторон лежат на одной прямой (теорема Паскаля). (3) 61. Докажите, что точки А, В, С лежат на одной прямой (рис. 123). (3) 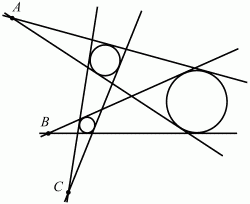 Рис. 123. 62. Пусть точка А расположена внутри круга радиуса R на расстоянии а от его центра. BB1 – произвольная хорда, проходящая через А. Тогда произведение ВА ? АВ1 постоянно и ВА ? АВ1 = R2– а2. Докажите, что если точка А лежит вне круга, то ВА ? АВ1 = а2 – R2. (3) 63. Докажите, что центр описанной окружности, точка пересечения медиан и точка пересечения высот лежат на одной прямой (теорема Эйлера). (3) 64. Докажите, что в остроугольном треугольнике точка пересечения высот является центром окружности, вписанной в треугольник, вершинами которого являются основания высот данного треугольника. (3) 65. Докажите, что для треугольника: 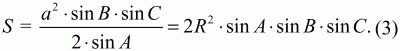 66. Даны две точки А и В. Докажите, что геометрическим местом точек М таких, что AM: ВМ = k (к ? 1), является окружность с центром на прямой АВ (окружность Anолонния). (3) 67. Найдите углы четырёхугольника ABCD (рис. 124). (3) 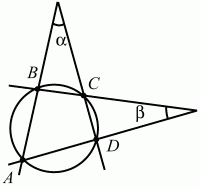 Рис. 124. 68. В треугольнике ABC отрезок А1B1, соединяющий основания высот АА1 и ВВ1, виден из середины стороны АВ под углом ?. Найдите величину угла С этого треугольника. (3) 69. Стороны треугольника равны а, b, с. В каком отношении делятся биссектрисы треугольника точкой их пересечения? (3) 70. Докажите, что расстояние между центрами вписанной и описанной окружностей (речь идёт о треугольнике) равно 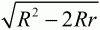 (формула Эйлера). (3) 71. Докажите, что в любом треугольнике основания высот, середины сторон и середины отрезков, соединяющих ортоцентр с вершинами, лежат на одной окружности радиуса R/2 (окружность девяти точек). Где находится центр данной окружности? Какое свойство есть у этой окружности? (3) 72. Докажите, что если прямая, не проходящая через вершины треугольника ABC, пересекает его стороны (прямые, содержащие стороны) АВ, ВС, СА соответственно в точках A1, B1 С1 то середины отрезков АА1, ВВ1, СС1 лежат на одной прямой (теорема Гаусса). (3) 73. Докажите, что если прямые АА1, ВВ1, СС1, соединяющие вершины треугольников ABC и A1B1C1, пересекаются в одной точке S или параллельны, то точки пересечения прямых АВ и А1В1, ВС и В1С1, АС и A1C1 (если они существуют) лежат на одной прямой (теорема Дезарга). Докажите обратную теорему. (3) 74. Докажите, что касательные в вершинах неравнобедренного треугольника к описанной около него окружности пересекают прямые, содержащие противоположные стороны этого треугольника, в трёх точках, лежащих на одной прямой (теорема Паскаля). (3) 75. Докажите теорему косинусов для четырёхугольника. (3) 76. Докажите, что для любого треугольника R ? 2r, причём равенство возможно только для равностороннего треугольника. (3) 77. Выведите координатные формулы движений плоскости. (3) I. Для параллельного переноса: х' = х + а y' = у + b. II. Для центральной симметрии: x' = 2x0 – x y' = 2y0 – y. III. Для поворота: х' = х ? cos? – у sin? y' = х ? sin? + у ? cos?. IV. Для осевой симметрии (уравнение прямой ах + by + с = 0): 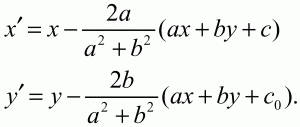 78. Докажите, что если точки А, В, С лежат на одной прямой, а точки А1, В1, С1 – на другой, и АВ1||А1В, ВС1||В1С, то АС1||А1С (теорема Паппа). (3) 79. Выведите координатные формулы инверсии: 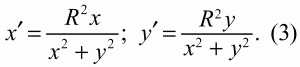 |
|
|||
|
Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх |
||||
|
|
||||
