Глава 42. ВИКТОР АЙГЕН, МАТЕМАГ И ВОЛШЕБНИК

В последнее время все больше фокусников-любителей стало обращать внимание на «матемагию» — фокусы, основанные не на ловкости рук, а на том или ином математическом принципе. Профессионалы не любят таких фокусников и стараются их избегать, потому что для обычной аудитории они слишком трудны и непонятны («ученая материя»!), но в небольшой компании, если их показывать не как чудеса, а просто как головоломки, такие фокусы могут быть интересными и занимательными. Мой друг Виктор Айген, инженер по электронному оборудованию и экс-президент «Братства американских повелителей волшебной палочки», всегда находится в курсе последних достижений матемагии. В надежде почерпнуть у него что-нибудь интересное для странички «Математических развлечений», регулярно публикуемой в журнале Scientific American, я нанес ему очередной визит.

Дверь открыл сам хозяин, стройный седовласый человек лет пятидесяти с небольшими морщинками у глаз.

— Не возражаешь, если мы немного посидим на кухне? — спросил он, впуская меня в квартиру. — Жена смотрит телепередачу, и, пока программа не кончится, ее лучше не беспокоить. Налить тебе бурбон-виски?

Мы сели за кухонный столик и подняли стаканы.

— За матемагию! — сказал я. — Что новенького?

Виктор тотчас же извлек из кармана рубашки колоду карт.

— Последняя новинка в карточных фокусах — это принцип Гилбрейта — одна довольно хитрая теорема, открытая Норманом Гилбрейтом, молодым фокусником из Калифорнии.

Разговаривая, Виктор быстро разложил карты на столе так, что черные и красные масти чередовались друг с другом.

— Ты, конечно, знаешь, что если снять часть колоды, взять одну половину колоды в правую руку, другую — в левую и предоставить картам падать одна на другую, то расположение карт будет весьма далеким от случайного?

Я снял верхнюю часть колоды и перетасовал карты по способу Виктора.

— Посмотри на карты, — сказал Виктор. — Видишь, правильное чередование черных и красных карт не нарушилось.

— Вижу.

— Сними карты еще раз, но так, чтобы нижняя карта верхней половины и верхняя карта нижней половины были одного цвета.

Обе половинки порознь передай мне. Карты держи рубашкой кверху, чтобы я не видел их лицевой стороны.

Я послушно выполнил все указания. Виктор опустил обе половинки под стол, так что никто из нас не мог видеть карт, и сказал:

— Я пытаюсь на ощупь определить цвет карт и составить черно-красную пару.

Нужно ли говорить, что первая же пара карт, которую он выложил на стол, была черно-красной. За первой парой последовала вторая, третья… десятая.

— Как ты это делаешь?

Виктор, не дав мне договорить, засмеялся. Бросив оставшиеся карты на стол, он начал открывать одну пару карт за другой. В каждой паре одна карта была красного, а другая — черного цвета.

— Нет ничего проще, — сказал он и пояснил: — Карты нужно снять, верхнюю часть карт положить снизу, а затем — запомни, это самое главное — разделить колоду на две части так, чтобы разделенными оказались две карты одного цвета. Чередование карт нарушится, но карты будут по-прежнему упорядочены и в каждой паре сохранится по одной черной и по одной красной карте.

— Не может быть!

— Подумай немного и ты поймешь, почему так получается, хотя сформулировать доказательство в нескольких словах не так легко. Кстати сказать, мой друг Эдгар Н. Джилберт из лаборатории фирмы «Белл» включил интересную головоломку, основанную на аналогичном принципе, в свою недавнюю работу о тасовании карт и теории информации. Я набросал ее для тебя.

С этими словами он протянул мне листок бумаги, на котором означились буквы:

TLVEHEDINSAGMELRLIENATGOVRAR

GIANESTYOFOFIFFOSHHRAVEMEVSO

— Эти буквы взяты из одной фразы, опубликованной в Scientific American пять лет назад, — пояснил он. — Джилберт написал каждую букву на отдельной карточке, а карточки сложил в колоду так, что всю фразу можно было прочитать, двигаясь сверху вниз.

Разделив колоду на две части и поменяв их местами, он записал новую последовательность, в которой расположились буквы. По его наблюдениям, на расшифровку фразы в среднем уходит около получаса. Дело в том, что, сняв карты, мы лишь незначительно меняем информацию, содержащуюся в исходной последовательности карт, а избыточность различных буквенных комбинаций в английском языке настолько велика, что вероятность составить фразу, отличную от первоначальной, крайне мала (в своей работе Джилберт даже приводит точное значение этой вероятности).

Я загремел кубиками льда в своем стакане.

— Прежде чем наполнить стаканы, — сказал Виктор, — я хочу показать тебе один остроумный фокус с предсказанием. Нам потребуется твой стакан и девять игральных карт. — И он разложил на столе девять карт со значениями от единицы до девятки в виде известного магического квадрата 3x3 (рис. 216).

Рис. 216 Карты и стакан, приготовленные для фокуса с предсказанием.

Все карты были червовой масти, только в центре лежала пятерка пик. Из кармана Виктор достал конверт и положил его рядом с магическим квадратом.

— Я хочу, чтобы ты поставил свой стакан на любую из этих девяти карт, — продолжал он, — но сначала я должен сообщить тебе, что в этом конверте лежит библиотечная карточка, на которой записаны кое-какие инструкции. Составляя их, я исходил из предположения о том, какую карту ты выберешь и как ты будешь переставлять свой стакан потом, когда карты нужно будет выбирать случайным образом. Если мои предположения верны, ты закончишь на карте в центре квадрата.

Он постучал пальцем по пятерке пик.

— А теперь можешь поставить стакан на любую из девяти карт, в том числе и на пятерку пик.

Я поставил стакан на двойку червей.

— Так я и думал, — засмеялся Виктор. Он вытащил из конверта карточку, и я прочитал следующие инструкции:

1. Отбрось семерку.

2. Сделай семь ходов и отбрось восьмерку.

3. Сделай четыре хода и отбрось двойку.

4. Сделай шесть ходов и отбрось четверку.

5. Сделай пять ходов и отбрось девятку.

6. Сделай два хода и отбрось тройку.

7. Сделай один ход и отбрось шестерку.

8. Сделай семь ходов и отбрось туза.

«Ход» состоит в передвижении стакана на соседнюю карту по вертикали или горизонтали, но не по диагонали. Тщательно следуя полученным инструкциям, я старался делать все ходы как можно более случайным образом.

К моему величайшему удивлению, стакан ни разу не оказался на той карте, которую я должен был отбросить, а после того, как я изъял восемь карт, мой стакан, как и предсказывал Виктор, остался стоять на пятерке пик!

— Ты совсем закрутил мне голову, — признался я. — А какую бы карту нужно было отбросить, если бы я поставил стакан на семерку пик?

— Должен признаться, — ответил Виктор, — что в этом фокусе есть немного жульничества, не имеющего отношения к математике.

Расположение карт в виде магического квадрата не имеет никакого отношения к делу. Существенно лишь, где лежат карты: карты, лежащие на нечетных местах — в углах и в центре, — образуют одно множество, карты, лежащие на четных местах, образуют множество противоположной четности. Увидев, что ты поставил стакан на карту из нечетного множества, я дал тебе те инструкции, которые ты видел. Если бы ты поставил стакан на карту из четного множества, то я бы, прежде чем вынимать карточку с инструкциями, перевернул конверт.

Он перевернул библиотечную карточку. На ее обратной стороне оказался второй перечень инструкций:

1. Отбрось шестерку.

2. Сделай четыре хода и отбрось двойку.

3. Сделай семь ходов и отбрось туза.

4. Сделай три хода и отбрось четверку.

5. Сделай один ход и отбрось семерку.

6. Сделай два хода и отбрось девятку.

7. Сделай пять ходов и отбрось восьмерку.

8. Сделай три хода и отбрось тройку.

— И ты считаешь, что эти два свода инструкций — один для случая, когда я ставлю стакан на четное место, другой — на нечетное, — всегда приведут к пятерке пик?

Виктор кивнул.

— Почему бы тебе не напечатать обе стороны карточки с инструкциями в журнале? Пусть читатели поломают голову над тем, как получается этот фокус.

Наполнив еще раз стаканы, Виктор сказал:

— Принцип четности используется во многих математических фокусах. Сейчас я покажу тебе один из них. У тебя создастся впечатление, что я обладаю даром ясновидения.

Он протянул мне карандаш и чистый лист бумаги.

— Сейчас я повернусь к тебе спиной, а ты нарисуешь самую затейливую замкнутую кривую с любым числом самопересечений (постарайся, чтобы их было побольше). Следи только за тем, чтобы ни в одной точке кривая не пересекала себя больше одного раза.

Он повернулся лицом к стене и оставался сидеть так, пока я рисовал кривую (рис. 217).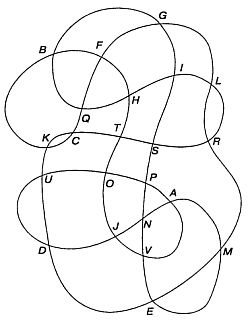

Рис. 217 Произвольно начерченная замкнутая кривая со случайным образом обозначенными точками самопересечения для фокуса с «ясновидением».

— Каждую точку самопересечения обозначь какой-нибудь буквой. Буквы не должны повторяться, — сказал он через плечо.

Я сделал все, как надо.

— Теперь поставь карандаш в любую точку кривой и начни обводить ее. Каждый раз, дойдя до точки самопересечения, называй вслух стоящую около нее букву. Делай так до тех пор, пока не обведешь всю кривую, но в одном месте — где именно, неважно — две соседние буквы поменяй местами. Под соседними я понимаю буквы, которые расположены рядом друг с другом в направлении обхода кривой. Когда будешь переставлять буквы, мне ничего не говори.

Я начал с точки N, дошел до Р и продолжил свой путь, называя одну за другой встречавшиеся мне буквы. Я видел, что Виктор записывает их в блокнот. Дойдя во второй раз до буквы В и увидев, что дальше стоит F, я мысленно переставил их и назвал сначала F, а потом В. При этом я называл буквы без промедления, в том же темпе, что и раньше, чтобы Виктор не мог догадаться, в каком именно месте я совершил перестановку.

Едва я успел закончить, как он сказал:

— Ты переставил В и F.

— Здорово! — ответил я. — Но как ты узнал?

Виктор засмеялся и повернулся ко мне.

— Этот фокус основан на одной топологической теореме, играющей важную роль в теории узлов, — сообщил он. — Превосходное доказательство ее можно найти в книге Г. Радемахера и О. Теплица.[66]

Он перебросил мне блокнот, в котором записывал буквы. Буквы попеременно располагались то над горизонтальной прямой, то под ней:

Если не переставлять буквы, то каждая из них должна встретиться один раз вверху, над прямой, и один раз внизу. Все, что мне нужно сделать, — это найти те буквы, которые повторяются дважды вверху и внизу. Именно их и переставили.

— Красивый фокус, — согласился я.

Виктор открыл пачку крекеров и, вытащив две штуки, положил их справа и слева от себя. На обоих крекерах он нарисовал стрелки, указывающие на север (рис. 218). Зажав левый крекер между большим и средним пальцами левой руки так, как показано на рис. 218, он кончиком указательного пальца правой руки надавил на угол А и повернул крекер вокруг диагонали, соединяющей зажатые углы.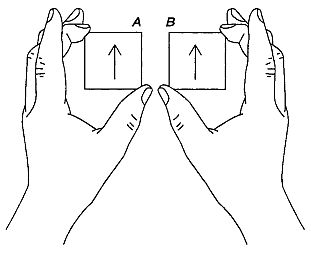

Рис. 218 Как держать крекеры в фокусе со стрелками, изменяющими направление.

На обратной стороне Виктор нарисовал еще одну стрелку, также указывающую на север.

Затем он взял в правую руку другой крекер и, повернув его нажатием указательного пальца на угол В, нарисовал на обратной стороне стрелку, указывающую на юг.

— Теперь у нас все готово, — сказал он улыбаясь, — для забавного фокуса, использующего свойства симметрии квадрата относительно вращений. Обрати внимание, что на обеих сторонах левого крекера я нарисовал стрелки, указывающие на север.

Он взял крекер в левую руку и повернул его несколько раз, чтобы продемонстрировать, что обе стрелки смотрят на север.

— На правом же крекере одна стрелка указывает на юг, а другая — на север. — Взяв крекер в правую руку и быстро завертев его, он показал, что стрелки действительно направлены в противоположные стороны.

Положив оба крекера на стол, Виктор осторожно, не изменив ориентации стрелок, поменял крекеры местами.

— Покрути их, пожалуйста, — попросил он. — Я хочу, чтобы ты убедился, что на правом крекере обе стрелки указывают на юг, а на левом — одна на юг, а другая на север.

Виктор передал мне оба крекера, и, повертев их точно таким же образом, как это делал он сам, я убедился, что крекеры действительно поменялись местами.

Виктор положил крекеры перед собой, простер над ними ладони и повелел крекерам незримо вернуться на прежние места. Он повернул крекер, лежащий слева от него, и я с удивлением увидел, что обе стрелки указывают на север! Виктор взял правый крекер, и оказалось, что одна стрелка смотрит на юг, а другая — на север!

— Попробуй сам, — сказал он, — и увидишь, что все получается автоматически. В самом деле, ведь оба крекера совершенно одинаковы. Разница состоит лишь в том, какой рукой ты их держишь.

Если попросишь зрителя проверить крекеры, то можешь не сомневаться, что он возьмет правый крекер в левую руку, а левый крекер — в правую. При этом крекер с противоположно направленными стрелками он возьмет так, чтобы стрелка на лицевой стороне была обращена на север.

Я допил свой стакан. Виски в бутылке оставалось только на одну порцию. Кухня слегка покачивалась.

— А сейчас я покажу тебе фокус, — сказал я, взяв из пачки еще один крекер, — статистическое испытание. Я подброшу крекер.

Если он упадет нижней стороной вверх, остатки виски получаешь ты. Если он упадет вверх другой стороной, виски допиваешь снова ты. Если же он упадет вверх ни той, ни другой стороной, то последнюю порцию получаю я.

Виктор смотрел на меня настороженно.

— О'кей! — сказал он.

Я сжал крекер в кулаке и подбросил вверх крошки.

Мертвая тишина. Даже холодильник перестал бормотать.

— Вижу, что виски, которое я должен был выпить, бросилось тебе в голову, — сказал наконец Виктор без тени улыбки. — И должен заметить, что такой дурацкий фокус вряд ли стоит показывать старому другу.

* * *

Нестрогое доказательство принципа Гилбрейта можно провести следующим образом. Сняв часть карт (из заранее подготовленной колоды с правильным чередованием черных и красных карт), мы окажемся в одной из двух возможных ситуаций: нижние карты в каждой из половин колоды могут быть либо одного цвета, либо двух разных цветов. Предположим, что нижние карты различаются по цвету.

После того как упадет первая из нижних карт, нижние карты в обеих половинах колоды станут одного цвета. Если первая упавшая карта была черной, обе нижние карты будут красными; если же она была красной, то обе нижние карты после этого будут черными. Поэтому безразлично, из какой половины брать следующую карту — из правой или из левой. И в том и в другом случае, уронив на стол следующую нижнюю карту, мы получим пару карт различного цвета. После того как упадет вторая карта, мы возвращаемся к исходной ситуации: нижние карты в обеих половинах колоды имеют разный цвет. Уронив на стол любую из них, мы снова добьемся того, что обе нижние карты будут одного цвета, противоположного цвету только что выложенной карты, и т. д. Рассуждение можно повторять до тех пор, пока вся колода не окажется исчерпанной.

Предположим теперь, что при первоначальном разбиении колоды на две части нижние карты каждой из половин оказались одного цвета. Первой может упасть любая из этих карт. Ко всем последующим парам карт применимо только что проведенное рассуждение.

Останется лишь одна карта. Ясно, что цвет ее должен отличаться от цвета отложенной в самом начале карты. Поэтому в том случае, когда колоду карт делят между двумя картами одного цвета (то есть между «готовыми» парами карт различных цветов), верхнюю и нижнюю карту колоды нужно объединить в одну пару, а все остальные пары уже готовы.

Фокус с картами и стаканом можно показывать многими способами. Один из читателей рассказал, что он, случайным образом выбрав девять карт, раскладывал их в три ряда по три карты в каждом, а потом просил зрителя поставить на любую из карт миниатюрный череп. В черепе было небольшое отверстие, в которое он вставлял скатанную полоску бумаги со своим предсказанием: названием карты, находящейся в центре. Карточку с нужными инструкциями он вынимал из кармана (в двух карманах, правом и левом, лежали две разные карточки). Указания, содержавшиеся в инструкциях, относились не к названию карты, а к ее «координатам».

Другой читатель разработал вариант фокуса, в котором инструкции зрителю давал голос, записанный на граммофонную пластинку, а стакан или другой предмет нужно было переставлять по девяти карточкам, носившим названия девяти планет. Пластинку, разумеется, можно было ставить либо на одну, либо на другую сторону.

Ответ

Предложение, записанное на карточках, расшифровывается так:

«The smelling organs of fish have evolved in a great variety of forms»

(«Органы обоняния рыбы чрезвычайно разнообразны по форме»).

Примечания:

6

Хэггис — шотландское национальное блюдо, которое готовится из овечьей или телячьей требухи и овсяной муки, приправленных луком и перцем.

66

Радемахер Г., Теплиц О. Числа и фигуры. Опыты математического мышления: 4-е изд. — М.: Наука, 1966.