Глава 36. ТЕОРИЯ ГРУПП И КОСЫ

Понятие «группы» — одно из основных понятий современной алгебры, охватывающее общие свойства самых разнообразных объектов различной природы и служащее неоценимым средством исследования в физике. Джеймс Р. Ньюмен сравнивал его с улыбкой Чеширского Кота:[57] когда Чеширский Кот (алгебра в том виде, как ее обычно преподают в школе) исчезает, остается только его абстрактная улыбка. Но улыбка подразумевает нечто веселое, занимательное. Может быть, теория групп покажется нам менее загадочной, если мы не будем воспринимать ее слишком серьезно.

Трое программистов — Эймз, Бейкер и Кумбс — хотят решить, кому из них платить за пиво. Разумеется, они могли бы бросить монетку, но предпочитают случайный выбор, основанный на игре, которая состоит в блуждании по некоторой сети линий. На листе бумаги проведены три вертикальные линии (назовем их основой).

Один из программистов, держа лист так, чтобы его друзья не видели, что он делает, обозначает эти линии наугад буквами А, В и С (рис. 180, а).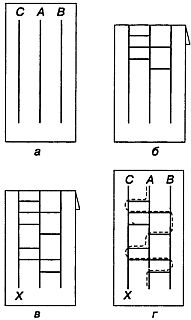

Рис. 180 Блуждание по линиям «основы» и «утка».

Верхний край листа он загибает так, чтобы буквы не были видны. Второй программист наугад проводит ряд горизонтальных линий (назовем их утком), каждая из которых соединяет какие-нибудь две вертикальные линии (рис. 180, б). Третий программист добавляет еще несколько горизонтальный линий, а у одной из вертикальных линий снизу ставит букву X (рис. 180,в).

Лист бумаги разворачивают. Эймз ставит свой палец в верхнюю точку линии А и начинает обводить ее сверху вниз. Дойдя до начальной или конечной точки линии утка (если точка пересечения вертикальной линии с линией утка лежит внутри горизонтального отрезка, Эймз ее пропускает и следует дальше), он поворачивает и проходит всю эту линию до другого ее конца, после чего снова поворачивает и продолжает спускаться вниз до тех пор, пока снова не встретит начальную или конечную точку другой линии утка. Так продолжается, пока он не достигнет нижней точки какой-нибудь вертикальной прямой. Если его путь (на рис. 180,г он показан пунктирной линией) заканчивается не в точке X, то за пиво платит не он. Затем точно таким же способом по сети прямых путешествуют Бейкер и Кумбс. Путь Бейкера заканчивается в точке X, поэтому за пиво приходится платить ему. Каким бы ни было число линий основы (вертикальных прямых), независимо от того, как проведены линии утка (горизонтальные прямые), пути игроков всегда заканчиваются на различных прямых, и никакие два маршрута никогда не приводят к одной и той же линии.

При более подробном рассмотрении этой игры выясняется, что в основе ее лежит одна из простейших групп — так называемая группа перестановок трех элементов. Что же такое группа? Это некая абстрактная структура, состоящая из множества элементов (а, Ь, с….), относительно природы которых не делается никаких предположений, с единственной бинарной операцией (ее мы обозначим символом о), сопоставляющей каждой паре элементов множества некоторый третий элемент. Чтобы такая структура составляла группу, должны выполняться следующие четыре условия:

1. Каждой паре элементов множества операция ставит в соответствие некоторый элемент того же множества. Это свойство носит название «замкнутости» множества относительно операции.

2. Операция подчиняется «ассоциативному закону»:

(а о Ь) о с = а о (b о с).

3. Существует элемент е (называемый «единицей»), такой, что

а о е = е о а = а.

4. Для каждого элемента а существует обратный элемент а', такой, что

а о а' = а' о а = е.

Если помимо только что названных четырех условий операция подчиняется еще и коммутативному закону:

а о Ь = b о a,

то группа называется коммутативной, или абелевой.

Целые числа — положительные, отрицательные и нуль — образуют группу относительно сложения (это наиболее известный пример группы). Множество целых чисел замкнуто относительно сложения (прибавить 2 к 3, а затем к 4 — то же самое, что прибавить 2 к сумме чисел 3 и 4); «единицей» группы служит 0, а элементом, обратным (или, как говорят еще, противоположным) целому положительному числу, — то же число, взятое со знаком минус. Группа целых чисел относительно сложения — абелева (2 + 3 = 3 + 2). Если в качестве операции выбрать деление, то целые числа не будут образовывать группы: поделив 5 на 2, мы получим 2,5, а это число не принадлежит множеству целых чисел.

Выясним теперь, с какой группой связана задача о блуждании по линиям «утка и основы». Шесть основных «преобразований» — элементов нашей конечной группы — изображены на рис. 181.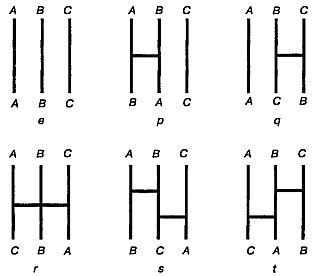

Рис. 181 Шесть элементов группы, возникающей в задаче о блуждании по сети линий.

Преобразование р «переводит стрелку»: начав двигаться по прямой А, вы закончите свой путь на прямой В и, наоборот, начав путь по прямой В, вы в конце концов окажетесь на прямой А (зато, попав напрямую С, вы останетесь на ней до конца). Преобразования q, r, s и t задают другие перестановки начал и концов различных путей.

Преобразование е в действительности ничего не меняет, но математики все равно называют его «преобразованием» в том же смысле, в каком пустое множество, не содержащее ни одного элемента, называют множеством. Для того чтобы выполнить преобразование е, не нужно проводить вообще никаких горизонтальных линий; это «тождественное» преобразование, которое в действительности ничего не преобразует. Шесть элементов группы соответствуют шести различным перестановкам трех символов. Групповая операция, обозначенная символом о, заключается в последовательном выполнении одного преобразования за другим, в добавлении к горизонтальной линии одного преобразования горизонтальной линии следующего преобразования.

Нетрудно проверить, что все свойства группы соблюдены. Множество преобразований замкнуто относительно операции «добавление горизонтальных линий» потому, что какую бы пару его элементов мы ни взяли, концы линий А, В и С окажутся переставленными так же, как и в результате применения к прямым А, В и С одного из шести преобразований. Например, р о t = r, так как, выполнив вслед за преобразованием р преобразование t, мы получим в точности такое же расположение концов линий А, В и С, какое получается при действии лишь одного преобразования г. Добавление горизонтальных линий, очевидно, ассоциативно (то есть, имея три горизонтали, мы можем сначала построить две первые, а затем пристроить к ним третью, но можем действовать и иначе: сначала провести две последние, посмотреть, как выглядит их «сумма», и добавить ее к первой горизонтали; в том и в другом случае результат будет одинаков). Если не проводить никаких горизонталей, то получится единичное, или тождественное, преобразование. Элементы р, q и r совпадают с обратными им элементами, а каждый из элементов s и t обратен другому. (Выполнить вслед за одним преобразованием другое, ему обратное, все равно, что вообще не проводить новых горизонтальных линий.) Полученная группа неабелева (например, если выполнить сначала преобразование q, a потом преобразование р, то результат получится совсем иным, чем в том случае, когда сначала выполняется преобразование р и лишь затем — преобразование q).

Полное описание строения этой группы видно из рис. 182.

Рис. 182 Результаты последовательного выполнения двух преобразований из группы, возникающей в задаче о блуждании по сети линий.

Что получится, если вслед за преобразованием r проделать преобразование s? Найдем букву r среди букв, выписанных слева от таблицы, и букву s среди букв, выписанных сверху. На пересечении r-й строки и s-ro столбца стоит буква р. Иначе говоря, добавив к горизонтальным линиям преобразования r горизонтальные линии преобразования s, мы получим такую же перестановку нижних концов вертикальных линий А, В и С, какая возникает, если провести горизонтальные линии одного лишь преобразования р. Эта чрезвычайно простая группа возникает во многих местах. Например, если обозначить тремя различными буквами вершины равностороннего треугольника, а затем произвести над ним все повороты и отражения, в результате которых он совмещается с самим собой, то окажется, что различных преобразований имеется только шесть и они образуют в точности такую же группу, как только что описанная.

Не обязательно вникать в тонкости теории групп, чтобы интуитивно понять, что, блуждая по сети, никакие два игрока не могут закончить свой путь на одной и той же вертикали. Вообразим, что три вертикальные линии — это просто-напросто три веревки. Каждый раз, проводя горизонтали, мы как-то переставляем нижние концы вертикалей, но точно такого же результата мы достигнем, если перевьем две веревки так, как это делают с прядями волос при заплетании косы. Ясно, что, как бы вы ни заплетали косу и какой бы длинной она ни была, дойдя до ее конца, вы всегда сможете различить все три пряди.

Представим себе, что и мы заплетаем девичью косу из трех прядей. Схематически последовательные перестановки прядей можно изобразить в виде сети (аналогичной той, которой мы пользовались в задаче о трех программистах), но при этом останется неясным, какие пряди оказываются сверху, а какие — снизу. Пригодна ли теория групп для описания действий, производимых нами при заплетании косы, с учетом этого усложняющего топологического фактора? Оказывается, вполне пригодна. Впервые это доказал немецкий математик Эмиль Артин. В его изящной теории кос элементами группы (их бесконечно много) служат «схемы переплетания», а групповой операцией, так же как в задаче о блуждании по сети линий, — последовательное применение одной схемы за другой.

Роль единичного элемента играет схема переплетения, состоящая из трех отдельных вертикалей — не переплетенных между собой прядей («косу еще не начинали заплетать»). Чтобы найти элемент группы, обратный какой-нибудь схеме переплетения, нужно просто взять зеркальное отражение этой схемы. На рис. 183 показана простенькая схема, взятая вместе с обратной ей схемой.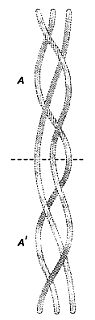

Рис. 183 Коса А — зеркальное отражение косы А'.

Если косу заплести сначала по «прямой», а потом по обратной схеме, то достаточно очевидно, что результат будет топологически эквивалентен заплетанию по единичной схеме: стоит лишь слегка потянуть за конец косы, изображенной на рис. 183, как все ее пряди расплетутся и выпрямятся. (Многие фокусы с распутыванием шнурков и веревочек основаны именно на этом небезынтересном групповом свойстве. Об одном из наиболее эффективных фокусов такого рода мы рассказали в главе 22.) В своей теории кос Артин не только впервые произвел классификацию всех мыслимых типов кос, но и предложил метод, позволивший узнавать, эквивалентны топологически или нет любые две сколь угодно сложные схемы переплетения.

Теория кос имеет самое непосредственное отношение к необычной игре, изобретенной все тем же датским поэтом, писателем и математиком Питом Хейном. Вырежьте из плотного картона кусочек в форме геральдического щита (рис. 184).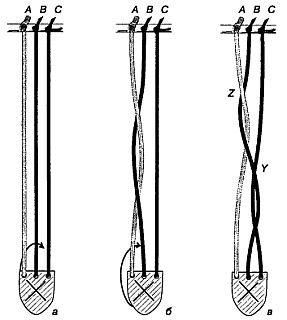

Рис. 184 Полный оборот подвески а по стрелке порождает косу б. Перевернув подвеску по стрелке еще раз, мы получим косу в.

Этот кусочек мы будем называть подвеской. Поскольку нам понадобится различать стороны подвески, их лучше всего раскрасить в разные цвета или одну из сторон пометить буквой X. У прямого края подвески проделайте три отверстия и, пропустив в каждое из них по отрезку тяжелого, но гибкого шнура длиной около 60 см, завяжите шнурки узлом (великолепно подходит для этих целей крученый шнур, из которого делают пояса). Другой конец каждого шнура привяжите к какому-нибудь неподвижному предмету, например к спинке стула.

Подвеска, как нетрудно видеть, может совершать полные обороты шестью различными способами: ее можно поворачивать на 360° вокруг вертикальной оси; поворачивать вокруг прямого края на себя или от себя, продевая ее между шнурами А и В; поворачивать также вокруг прямого края на себя или от себя, но продевать при этом между шнурами В и С. Во всех шести случаях получаются разные косы. Коса, которая «заплетается» при пропускании подвески между шнурами В и С, показана на рис. 184,б. Возникает вопрос, можно ли расплести эту косу, продевая подвеску между шнурами подобно ткацкому челноку и все время держа ее в плоскости рисунка— так, чтобы сторона, помеченная буквой X, была обращена к зрителю, а острый «носик» смотрел на вас (предполагается, что, читая, вы держите книгу на столе перед собой)? Оказывается, что реворачивание разрешается производить в любом направлении как на себя, так и от себя), всегда можно расплести, действуя подвеской как ткацким челноком, без новых поворотов ее; если же коса получилась оттого, что подвеска совершила нечетное число полных оборотов, то расплести ее без дополнительных оборотов подвески никогда не удастся.

Хейн впервые услышал об этой теореме в начале тридцатых годов на одном семинаре в Институте теоретической физики Нильса Бора, когда П. Эренфест обсуждал ее в связи с какой-то проблемой квантовой теории. С помощью ножниц, принадлежавших супруге Бора, и нескольких веревочек, привязанных к спинке стула, Хейну и другим участникам семинара удалось найти доказательство этой теоремы. Позднее Хейну пришло в голову, что вращающееся тело и окружающая его вселенная входят в задачу симметрично, поэтому симметричную модель можно было бы построить очень просто, привязав по подвеске к каждому концу шнура. Имея такую симметричную модель, можно вдвоем играть в топологическую игру. Каждый участник берет свою подвеску; между подвесками протянуты три шнура. Один из игроков заплетает косу, а второй, расплетая ее, засекает необходимое для этого время, затем игроки меняются ролями. Тот, кто расплетет косу быстрее, считается победителем.

Теорема о четном и нечетном числе поворотов подвески, очевидно, применима и к этой игре. Начинающим рекомендуется ограничиться косами, при заплетании которых подвеска совершает два полных оборота, и лишь потом, попрактиковавшись и набив руку, переходить к более сложным косам четного порядка. Хейн назвал свою игру «танглоид». В течение ряда лет она была очень популярна в Европе.

Почему между четным и нечетным числом полных оборотов подвески существует такое различие? На этот весьма непростой вопрос трудно ответить, не вдаваясь более глубоко в теорию групп.

Некоторое представление о причинах такого различия можно получить, заметив, что два поворота в противоположных направлениях—это то же самое, что ни одного поворота. Если два оборота почти противоположны и отличаются только тем, что при совершении их подвеска была пропущена между различными парами шнуров, то косу можно расплести, продев подвеску между шнурами так, чтобы уничтожить это различие. Пользуясь теорией кос, можно доказать, что при нечетном числе оборотов подвески пряди распутать нельзя.

Заплетать косы, поворачивая подвеску наугад четное число раз, а затем быстро расплетать их — занятие увлекательное. На рис. 185 показаны три простые косы, каждая из которых заплетена лишь двумя полными оборотами подвески.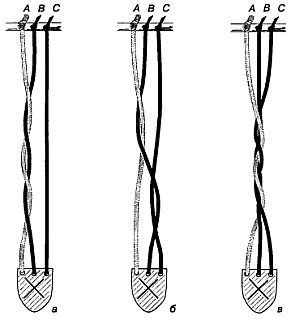

Рис. 185 Три задачи на расплетание кос.

Косу в случае а получили, дважды пропустив подвеску между шнурами В и С (оба раза от себя); в случае б — продев подвеску между шнурами В и С от себя, а затем между шнурами А и В в обратном направлении. Коса в случае в заплелась от того, что подвеску два раза повернули слева направо вокруг вертикальной оси. Читателю предоставляется самому найти лучший способ расплетания каждой из этих кос.

* * *

При изготовлении «реквизита» для танглоида подвеску лучше вырезать не из картона, а из деревянной дощечки или пластика.

Вместо трех отдельных шнуров Хейн рекомендует брать один длинный шнур. Шнур нужно пропустить через первое отверстие первой подвески и привязать к ней, чтобы он не выскальзывал. Затем его нужно продеть сквозь первое отверстие второй подвески и, пропустив в обратном направлении через среднее отверстие все той же второй подвески, продеть через среднее отверстие первой подвески, после чего продеть в обратном направлении через третье отверстие первой подвески и, продев сквозь третье отверстие второй подвески, завязать свободный конец шнура узлом. Шнур свободно может проскальзывать в отверстия, что облегчает все манипуляции по сравнению с конструкцией, в которой используются три отдельных шнура. Один читатель сообщил нам, что он соединил свои подвески тремя отрезками гибкого шнура и обнаружил, что это также облегчает все манипуляции. Игру можно усложнять, вводя все новые и новые шнуры, но и при трех шнурах она весьма непроста.

Из рис. 182 видно, что описывающая танглоид группа неабелева (то есть некоммутативна). Таблицы для абелевых групп симметричны относительно диагонали, идущей из левого верхнего в правый нижний угол. Иначе говоря, треугольные части таблицы, лежащие по обе стороны этой диагонали, служат зеркальным отражением одна другой.

Если в игру с блужданием по сети линий «основы» и «утка» играют не втроем, а вчетвером, то ее группой будет группа перестановок четырех символов. Эта группа не совпадает с группой, описывающей повороты и отражения квадрата, потому что некоторые перестановки вершин квадрата нельзя получить с помощью одних лишь поворотов и отражений. Преобразования квадрата образуют «подгруппу» группы перестановок четырех символов. Все конечные группы (то есть группы с конечным числом элементов) либо являются группами перестановок, либо входят как подгруппы в какую-нибудь из групп перестановок.

В статье Артина по теории кос[58] дается метод приведения любой косы к ее «нормальной» форме. Первая прядь «нормальной» косы полностью выпрямлена, вторая может охватывать первую прядь петлями, третьей пряди разрешается описывать петли вокруг первой и второй прядей и т. д. «Хотя доказано, что всякую косу можно привести к эквивалентной ей нормальной форме, — пишет Артин, — автор на собственном опыте убедился, что любая попытка осуществить предсказанное на живой персоне приводит лишь к бурным протестам с ее стороны и оскорбительным выпадам против математики».

Ответы

Три задачи «на расплетание» кос решаются следующим образом:

1. Пропустите подвеску под шнуром С справа налево, а затем под шнурами А и В слева направо.

2. Пропустите подвеску под серединой шнура В слева направо.

3. Пропустите подвеску под всеми шнурами слева направо.

Примечания:

'American Mathematical Monthly, 64, 1957, p. 143.

Чеширский Кот — один из персонажей известной сказки Льюиса Кэрролла "Алиса в Стране Чудес"

Artin E. Theory of Braids:.Annals of Mathematics, 48, № 1, January 1947, pp. 101–126.

Оглавление