Глава 34. ВЕРОЯТНОСТЬ И НЕОДНОЗНАЧНОСТЬ

Чарлз Сандерс Пирс как-то сказал, что ни в одной другой области математики специалист не ошибается так легко, как в теории вероятностей. История подтверждает справедливость этого замечания.

Так, Лейбниц считал, что число 12 при бросании двух игральных костей выпадает также часто, как и число 11. Великий французский математик XVIII века Даламбер полагал, что результаты троекратного бросания одной монеты отличаются от результатов бросания трех монет одновременно, и был убежден, что после длинной серии «орлов» вероятность выпадения «решки» повышается (эту уверенность многие любители азартных игр разделяют и поныне).

В наше время теория вероятностей дает на столь простые вопросы ясные и четкие ответы, но при выполнении одного непременного требования: в условии задачи должно быть точно определено, каким именно способом следует производить соответствующие испытания. Всякого рода неточности и умолчания служат причиной недоразумений и парадоксов во многих занимательных задачах вероятностного характера.

Классическим примером может служить задача о сломанной палке: палку случайным образом ломают на три части; какова вероятность того, что из обломков можно составить треугольник? Для того чтобы решить эту задачу, мы должны непременно уточнить, как именно разрешается ломать палку.

Один из возможных вариантов заключается в следующем. Будем считать, что точки перелома равномерно распределены по длине палки. Выберем из них наугад две и переломим палку в выбранных точках. При таком понимании «случайного» переламывания палки на три части ответ задачи, как нетрудно показать, исходя из наглядных геометрических представлений, равен 1/4.

Действительно, нарисуем равносторонний треугольник и соединим середины его сторон отрезками прямых. У нас получится равносторонний треугольник меньших размеров, расположенный внутри первого (на рис. 176 меньший треугольник заштрихован).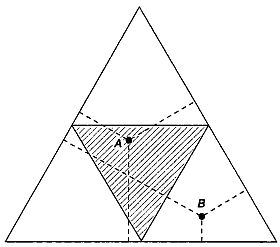

Рис. 176 Если палку разломать на три части, то из ее обломков с вероятностью 1/4 можно составить треугольник.

Сумма длин перпендикуляров, опущенных из любой точки большого треугольника на его стороны, не зависит от выбора точки и равна высоте большого треугольника. Если эту точку выбрать внутри меньшего треугольника (на рис. 176 этому условию удовлетворяет точка А), то любой из трех перпендикуляров будет не больше суммы двух других перпендикуляров. Следовательно, из отрезков, равных по длине трем перпендикулярам, опущенным из любой точки малого треугольника на стороны большого, всегда можно построить треугольник. Если же точка лежит вне малого треугольника (на рис. 176 —точка В), то один перпендикуляр заведомо длиннее суммы двух других перпендикуляров, и построить из таких перпендикуляров треугольник невозможно.

Мы не случайно привели здесь эту простую геометрическую задачу. Ее решение тесно связано с решением вероятностной задачи о сломанной палке. В самом деле, сумма трех перпендикуляров соответствует длине палки, каждая точка большого треугольника отвечает одному и только одному способу разломать палку на три части, а три перпендикуляра — трем обломкам. Вероятность сломать палку с «благоприятным исходом» равна вероятности случайного выбора такой точки, что три опущенных из нее перпендикуляра могут служить сторонами некоторого треугольника. Как мы только что видели, такое событие возможно лишь тогда, когда случайно выбранная точка попадает внутрь заштрихованного треугольника.

Так как его площадь составляет 1/4 площади всего треугольника, то искомая вероятность равна 1/4.

Утверждению о том, что «палку случайным образом ломают на три части», можно придать иной смысл. Например, его можно толковать так: палку наугад переламывают на две части, затем также наугад выбирают один из обломков и переламывают его еще раз (снова в случайно выбранной точке). С какой вероятностью в этом случае из обломков можно составить треугольник?

Решение задачи дает тот же чертеж, что и в предыдущем случае. Если, переломив палку в первый раз, мы выберем более короткий обломок, то построить треугольник будет невозможно. Что же произойдет, если выбрать обломок подлиннее? Пусть вертикальный перпендикуляр на чертеже соответствует короткому обломку.

Для того чтобы вертикальный перпендикуляр был меньше суммы двух других перпендикуляров, точка, из которой они опущены, не должна лежать внутри самого верхнего из малых треугольников, на которые отрезками прямых, соединяющих середины его сторон, поделен большой треугольник. Точки, у которых вертикальный перпендикуляр меньше суммы двух других перпендикуляров, равномерно заполняют три малых треугольника в нижней части большого треугольника. Благоприятному исходу по-прежнему соответствуют лишь те точки, которые попадают внутрь заштрихованного треугольника, но на этот раз его площадь составляет лишь 1/3 площади, отвечающей всем возможным исходам. Следовательно, выбрав из двух обломков больший, мы сможем построить треугольник (разломав выбранный нами обломок еще раз на две части) лишь в 1/3 случаев. Так как вероятность выбрать больший обломок равна 1/2, ответ на вопрос задачи в этом случае равен произведению 1/2 на 1/3, то есть 1/6.

Геометрическими построениями в задачах такого рода следует пользоваться осторожно, потому что они также способны вводить в заблуждение своей неоднозначностью. В качестве примера приведем одну задачу, рассмотренную в курсе теории вероятностей знаменитого французского математика XIX века Бертрана: какова вероятность того, что проведенная наудачу хорда будет длиннее стороны равностороннего треугольника, вписанного в ту же окружность?

Ответить на этот вопрос можно, например, так. Хорда должна начинаться в некоторой точке окружности. Обозначим эту точку через А и проведем к окружности касательную в точке А (рис. 177,a).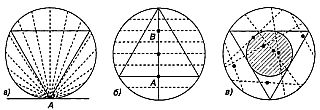

Рис. 177 Вероятность того, что наудачу проведенная хорда длиннее стороны вписанного равностороннего треугольника, оказывается 1/3 (a), 1/2 (б) и 1/4 (в).

Другим концом хорды может быть любая точка окружности, поэтому мы получаем бесконечно много равновероятных хорд (некоторые из них на чертеже показаны пунктиром). Ясно, что длиннее стороны вписанного равностороннего треугольника могут быть лишь те хорды, которые попадают внутрь угла при вершине треугольника в точке А. Поскольку этот угол равен 60°, а хорды заполняют развернутый угол (180°), вероятность того, что случайно проведенная хорда будет длиннее стороны вписанного равностороннего треугольника, равна 60/180, или 1/3.

Возможен и несколько иной подход к решению задачи Бертрана.

Какую бы хорду мы ни провели, она всегда будет перпендикулярна одному из диаметров окружности. Будем считать, что проведенная нами хорда перпендикулярна вертикальному диаметру, и впишем в окружность равносторонний треугольник с вершиной, совпадающей с верхним концом вертикального диаметра (рис. 177, б). Точки пересечения хорд, перпендикулярных данному диаметру, с ним самим равномерно распределены по всему диаметру. Некоторые из этих хорд проведены на чертеже пунктирными линиями. Нетрудно показать, что расстояние от центра окружности до точки А равно половине радиуса. Обозначим через В точку того же диаметра, лежащую на расстоянии половины радиуса по другую сторону от центра. Легко видеть, что длиннее стороны вписанного равностороннего треугольника будут лишь те хорды, которые пересекают проведенный диаметр между точками А и В. Так как отрезок АВ составляет половину диаметра, ответ задачи 1/2.

Возможен и третий подход к ее решению. Любую точку круга можно рассматривать как середину некоторой хорды. Из рис. 177, в видно, что длиннее стороны вписанного равностороннего треугольника могут быть лишь те хорды, середины которых лежат внутри маленького заштрихованного круга. Площадь заштрихованного круга составляет ровно 1/4 площади всего круга. Отсюда следует, что и ответ задачи в данном случае оказывается равным 1/4.

Естественно возникает вопрос: какой же из трех ответов правилен? Каждый ответ верен по-своему, каждый отвечает определенному способу проведения «случайных» хорд. Экспериментально соответствующие построения можно осуществить, например, с помощью следующих трех «методов»:

1. Взять два веретена и, закрутив каждое из них в любую сторону независимо от другого, по очереди поставить их в центр круга.

Отметить конечные точки траекторий, описанных остриями веретен, и соединить отмеченные точки прямой. С вероятностью 1/3 отрезок этой прямой, заключенной внутри круга, будет больше стороны вписанного равностороннего треугольника.

2. Нарисовать мелом на асфальте большой круг и с расстояния около 5 метров вкатывать в него палку от метлы. Оставшись где-то внутри круга, палка наметит направление некоторой хорды. С вероятностью 1/2 эта хорда длиннее стороны вписанного равностороннего треугольника.

3. Намазать круг медом и подождать, пока на него не сядет муха. Провести хорду, середина которой совпадает с точкой, где сидит муха. С вероятностью 1/4 эта хорда будет длиннее стороны вписанного равностороннего треугольника.

Каждый из предложенных способов построения «случайных хорд» вполне законен, поэтому наша задача в ее первоначальной формулировке допускает различные толкования. Однозначное решение становится возможным лишь после того, как мы уточним, в каком именно смысле следует понимать выражение «провести случайным образом хорду», дав точное описание метода ее построения. Разумеется, большинство людей, если попросить их провести наугад хорду в окружности, изберут для этого способ, не имеющий ничего общего ни с одним из трех перечисленных выше способов.

С вероятностью, много большей чем 1/2, человек проводит хорду, превышающую по длине сторону вписанного равностороннего треугольника.

Другим примером неоднозначности, возникающей из-за того, что в условии задачи ничего не говорится о способе получения интересующих нас сведений, может служить задача 2 из главы 29.

Читателю сообщается, что у мистера Смита двое детей, из которых по крайней мере один мальчик. Требуется вычислить вероятность того, что у мистера Смита два сына. Многие читатели правильно заметили, что ответ зависит от того, каким образом мы узнаем, что «по крайней мере один из детей мальчик». Если из всех семей, имеющих по два ребенка, из которых по крайней мере один мальчик, выбирать случайным образом какую-нибудь одну семью, то ответ равен 1/3. Однако, оставаясь в рамках того же условия, можно действовать иначе. Из общего числа семей, имеющих по два ребенка, выберем наугад какую-нибудь одну семью. Если оба ребенка мальчики, то мы сообщим тому, кто решает задачу, что «по крайней мере один из детей мальчик». Если в выбранной нами семье две девочки, мы скажем, что «по крайней мере один ребенок девочка».

Если же в семье один мальчик и одна девочка, то, выбрав кого-нибудь из них наугад, мы с полным основанием сможем заявить, что «по крайней мере один ребенок в этой семье мальчик (или девочка)» в зависимости от того, кто из ребят был выбран. При таком способе получения необходимых для решения данных вероятность того, что в семье имеются два мальчика или две девочки, очевидно, равна 1/2. (Действительно, утверждения делаются в каждом из четырех случаев: ММ, МД, ДМ, ДД; М здесь означает мальчик, Д — девочка, а «однотипные» пары ММ и ДД составляют ровно половину общего числа случаев.) О том, что даже выдающиеся математики иногда упускают из виду возможность неоднозначного толкования условий этой задачи, свидетельствует хотя бы тот факт, что она (в формулировке, не достаточной для получения совершенно определенного ответа) включена в один из лучших учебников высшей математики, изданных для колледжей.

Еще труднее точно сформулировать задачу о трех заключенных и тюремном надзирателе, которая получила широкую известность.

Она также приводит к неожиданным парадоксам.

Три узника А, В и С, приговоренные к смертной казни, сидели в одиночных камерах. Губернатор решил помиловать одного из них. Записав имена заключенных на трех листочках бумаги, он бросил листочки в шляпу и тщательно перемешал. Затем он вытащил один листочек, прочитал значившееся там имя и сообщил по телефону свое решение тюремному надзирателю, потребовав от того, чтобы имя счастливчика в течение еще нескольких дней хранилось в тайне. Слух о помиловании дошел до заключенного А. Во время утреннего обхода А попытался выведать у надзирателя, кто же помилован, но тот отказался отвечать на подобные вопросы.

— Тогда назовите, — попросил А, — имя одного из заключенных, которые будут казнены. Если помилован В, назовите мне имя С.

Если помилован С, назовите мне имя В. Если помиловали меня, то бросьте монетку, чтобы решить, кого назвать — В или С.

— Но если вы увидите, что я бросаю монетку, — ответил осторожный надзиратель, — то сразу узнаете, что помиловали именно вас, а увидев, что я не бросаю монетку, вы догадаетесь, что помиловали либо вас, либо того, чье имя я не назову.

— Хорошо, — сказал А, — можете ничего не говорить мне сейчас, ответьте на мой вопрос завтра.

Надзиратель, ничего не знавший о теории вероятностей, провел в размышлениях всю ночь и решил, что даже если он и примет предложение А, то это ничем не поможет А оценить свои шансы остаться в живых. Поэтому на следующее утро надзиратель сообщил А, что казни подлежит заключенный В.

Когда надзиратель ушел, А про себя посмеялся над глупостью тюремщика: ведь теперь то, что у математиков принято называть «пространством элементарных событий», состояло лишь из двух равновероятных элементов: губернатор мог помиловать либо С, либо самого А. Следовательно, по всем правилам вычисления условной вероятности шансы А остаться в живых возросли с 1/3 до 1/2.

Надзиратель не знал, что А мог перестукиваться с находившимся в соседней камере заключенным С по водопроводной трубе. А не замедлил подробно передать своему соседу все, о чем он спросил надзирателя и что тот ему ответил. Заключенный С также обрадовался новости, потому что, рассуждая так же, как А, он подсчитал, что и его шансы остаться в живых возросли до 1/2.

Правильно ли рассуждали оба узника? Если же нет, то как должен был вычислять свои шансы на помилование каждый из них?

* * *

Вряд ли можно найти более красноречивый пример того, насколько легко может ошибиться при подсчете вероятности даже специалист и насколько рискованно полагаться на наглядные геометрические представления, чем второй вариант приведенной нами задачи о сломанной палке. Помещенное выше решение заимствовано из задачника по теории вероятностей, такой же ответ можно обнаружить и во многих других старых учебниках теории вероятностей. И все же это решение совершенно неправильно!

В первом варианте задачи, когда палку ломают в двух одновременно выбранных точках, каждый акт такого разделения палки на три части изображается на чертеже точкой, и они в совокупности равномерно заполняют три нижних (малых) треугольника.

Уитворт предполагает, что во втором варианте задачи, когда палку сначала случайным образом переламывают пополам, а затем, выбрав более длинный обломок, переламывают и его, точки, изображающие результаты двух последовательных переламываний палки, также будут заполнять три нижних треугольника. Но это предположение неверно: во втором случае в средний треугольник точки будут попадать чаще, чем в два других.

Примем длину палки за 1 и обозначим через х длину более короткого обломка, получившегося после первого переламывания палки. Чтобы построить треугольник, мы должны переломить в какой-то точке больший обломок, длина которого составляет (A-х) единиц. Следовательно, вероятность построить треугольник составляет 1/(1-x). Усреднив по х от 0 до 1/2, мы получаем — 1 + 2 In 2, или 0,386. Сломав палку в первый раз, мы еще должны после этого выбросить более длинный обломок. Так как этот выбор мы производим с вероятностью 1/2, число 0,386 для получения окончательного ответа нужно умножить на 1/2. В результате мы получаем ответ задачи: 0,193. Это чуть больше 1/6 — ответа, к которому приводят предыдущие рассуждения.

После опубликования мною статьи, составляющей содержание этой главы, я получил любопытное письмо от сотрудников Отдела учебных тестов из Принстона. Прислав правильное решение второго варианта задачи о сломанной палке, они предложили мне ответить, какая из следующих трех гипотез наиболее вероятна:

1) м-р Гарднер честно заблуждается;

2) м-р Гарднер умышленно совершает ошибки в рассуждениях, чтобы испытать своих читателей;

3) м-р Гарднер виновен в том, что в математическом мире принято называть заблуждениями Даламбера.

Сообщаю: наиболее вероятна третья гипотеза.

Ответы

Ответ к задаче о трех смертниках: вероятность того, что помилован A, равна 1/3, вероятность того, что помилован С— 2/3.

Независимо от того, кто помилован в действительности, надзиратель сообщает А, что казнить собираются другого заключенного, поэтому, что бы ни сказал тюремщик заключенному А, вероятность остаться в живых для того по-прежнему остается равной 1/3.

Аналогичная ситуация возникает в следующей карточной игре.

Две черные карты (означающие смертный приговор) и одна красная карта (соответствующая помилованию) перетасовываются и сдаются трем игрокам А, В и С (заключенным). Если четвертый участник игры (надзиратель) заглянет во все карты, а затем откроет черную карту, принадлежащую либо В, либо С, то какова вероятность того, что у А красная карта? Трудно удержаться от искушения предположить, что искомая вероятность равна 1/2, так как нераскрытыми остались только две карты, лишь одна из которых черная. Но так как у одного из двух игроков, В или С, всегда должна быть черная карта, то показ ее не позволяет сделать никаких заключений о цвете карты, сданной игроку А.

Это нетрудно понять, если усугубить ситуацию — смертному приговору будет соответствовать туз пик в полной карточной колоде. Предположим, что карты сданы и А открывает одну из полученных им карт. Вероятность избежать смертного приговора для А равна 51/52. Если кто-нибудь заглянет в карты и откроет 50 карт, отличных от туза пик, то нераскрытыми останутся только две карты, одна из которых заведомо должна быть тузом пик, но это, очевидно, не понижает шансов А до 1/2. Не понижает потому, что, заглянув в 51 карту, мы всегда можем найти среди них 50 карт, значение которых отлично от туза пик. Поэтому, найдя и открыв их, мы не изменим вероятности того, что А не будет приговорен к смертной казни. Другое дело, если мы наугад раскрыли 50 карт и среди них не оказалось туза пик. В этом случае А с вероятностью 1/2 должен вытащить роковую карту.

А как обстоят дела у С? Либо А, либо С должен быть казнен.

Их вероятности выжить в сумме должны составлять 1. Шансы выжить у А равны 1/3; следовательно, С не будет казнен с вероятностью 2/3. Это подтверждается рассмотрением четырех возможных элементов в пространстве элементарных событий и их начальных вероятностей.

1. Помилован С, надзиратель назвал В (вероятность 1/3).

2. Помилован В, надзиратель назвал С (вероятность 1/3).

3. Помилован А, надзиратель назвал В (вероятность 1/6).

4. Помилован А, надзиратель назвал С (вероятность 1/6).

Узник А остается в живых в случаях 3 и 4; следовательно, вероятность счастливого исхода для А равна 1/3. Известие о том, что казни подлежит В, отвечает случаям 1 и 3. При этом случай 1 (вероятность 1/3) встречается вдвое чаще, чем случай 3 (вероятность 1/6). Следовательно, вероятность того, что помилован С, относится к вероятности помилования А как 2 к 1, то есть равна 2/3. В нашей карточной модели это означает, что с вероятностью 2/3 игрок С получает красную карту.

Задача о трех заключенных вызвала настоящий поток писем (мнения читателей разделились). К счастью, все возражения оказались безосновательными. Ниже приведен хорошо продуманный разбор этой задачи, принадлежащий ШеЙле Бишоп.

Сэр!

Прийти к заключению, что рассуждения А неверны, меня заставила следующая парадоксальная ситуация. Предположим, что первый разговор между А и его стражем был именно таким, как сказано в условии задачи, но когда тюремщик направлялся к камере А, чтобы сообщить тому о предстоящей казни В, то по дороге он провалился в люк или с ним приключилась какая-нибудь другая неприятность, помешавшая второму разговору с А.

В этом случае А мог бы рассуждать так: «Предположим, что надзиратель намеревался сообщить мне, что казнить собираются В. Тогда мой шанс остаться в живых был бы равен 1/2. С другой стороны, если бы надзиратель сообщил мне, что казнить должны С, то мои шансы не изменились бы и также составляли бы 1/2. Но мне достоверно известно, что он должен был сообщить мне либо одно, либо другое известие. Поэтому и в том и в другом случае с вероятностью 1/2 я должен остаться в живых». Итак, если рассуждать таким образом, то оказывается, что А мог бы подсчитать вероятность благоприятного для себя исхода (1/2), не спрашивая ни о чем своего тюремщика!

После нескольких часов размышления я наконец пришла к иному заключению. Рассмотрим большое число групп из трех узников, находящихся в той оке ситуации, что и А, В и С.

Пусть в каждой группе с тюремщиком беседует свой А. Если всего имеется 3n групп заключенных (по 3 человека в каждой группе), то в n из них будет помилован А, в n будет помилован В и в n будет помилован С. В 3n/2 случаях тюремщик скажет: «Будет казнен В». В n из этих случаев С будет выпущен на свободу, в n/2 случаях на свободу будет выпущен А. Шансы С вдвое больше шансов А. Следовательно, вероятности выжить для А и С равны соответственно 1/3 и 2/3…

Нашлись читатели, которые считают, что тюремного надзирателя незаслуженно оклеветали. Вот что написали двое из них:

Сэр!

Мы обращаемся к вам от имени надзирателя, который, являясь должностным лицом, не хотел бы быть замешанным в обсуждение спорных вопросов.

Вы порочите его репутацию, заявляя, будто надзиратель ничего не знал о теории вероятностей. Мы считаем, что подобное утверждение является величайшей несправедливостью. Вы заблуждаетесь, а быть может, и злостно клевещете. Со своей стороны мы хотим заверить вас, что математика вообще и теория вероятностей в частности в течение вот уже многих лет являются его излюбленнейшим занятием. То, что он, руководствуясь гуманным намерением облегчить последние часы осужденного человека (ибо, как известно теперь, помилован был С), ответил на вопрос А, ничуть не противоречит инструкциям, полученным им от губернатора.

Единственное, в чем его действительно можно упрекнуть (и за что он уже получил выговор от губернатора), так это то, что он не сумел воспрепятствовать установлению связи между А и С и тем самым не помешал С более точно оценить вероятность остаться в живых. Но и этот промах тюремщика не повлек за собой тяжких последствий, поскольку С не сумел должным образом воспользоваться полученной информацией.

Если вы публично не отречетесь от своих слов и не принесете извинений, мы будем вынуждены прекратить подписку на ваш журнал.