Глава 30. ИНДУКТИВНАЯ ИГРА ЭЛУЗИС

В большинстве математических игр, начиная с игры в крестики и нолики и кончая шахматами, от играющего требуется умение мыслить индуктивно. Совсем иные требования предъявляет элузис — замечательная карточная игра, изобретенная Робертом Эбботом.

Этот писатель из Нью-Йорка известен как создатель многих карточных и настольных игр, но элузис вызывает не только у математиков, но и у других ученых особый интерес. Дело в том, что игра элузис во многом напоминает исследование законов природы и позволяет тем, кто в нее играет, развивать интуицию, способность угадывать скрытые закономерности, то есть именно те качества, которыми и объясняются «внезапные озарения» и «наития», переживаемые творчески мыслящими личностями.

В элузис можно играть, когда соберется не меньше трех игроков. Для игры берут обычную[52] колоду игральных карт. Играющие сдают карты по очереди. Тот, кто должен сдавать карты, выполнив свою функцию, в дальнейшей игре активного участия не принимает и выступает лишь в роли наблюдателя или арбитра. Последнюю карту кладут посреди стола вверх картинкой. Это первая карта так называемого «исходного», или «начального», ряда. Для того чтобы никто из игроков не оказался обделенным и не получил меньше карт, чем другие, сдающий должен заранее подготовить колоду, изъяв из нее в случае необходимости лишние карты. Если играющих трое (имеются в виду все играющие, в том числе и тот, кто сдавал карты, хотя он не оставляет себе ни одной карты), то из колоды нужно заранее вынуть одну карту; при четырех играющих лишних карт нет; при пяти нужно вынуть три карты и т. д. Изъятые из колоды карты сдающий откладывает в сторону, не показывая их играющим.

После того как все карты сданы и первая карта «начального» ряда положена на свое место, сдающий втайне от остальных игроков задумывает правило, которого нужно придерживаться при выкладке карт в «исходном» ряду. Именно это правило и служит аналогом закона природы. В этом смысле, с точки зрения играющих, автор правила выступает в роли природы, или, если угодно, «всемогущего». Задуманное правило сдававший карты записывает на отдельном листке бумаги и, сложив его, откладывает в сторону.

Это нужно для того, чтобы по окончании игры ее участники могли убедиться в том, что «арбитр» во время игры не менял своего правила и не нарушал постоянства законов природы. Цель игры для каждого активного участника заключается в том, чтобы избавиться от как можно большего числа карт. Тому, кто правильно угадал записанное на листке правило, сделать это нетрудно.

Примером очень простого правила может служить хотя бы такое: «Если верхняя карта в исходном ряду красной масти, пойдите картой черной масти. Если же верхняя карта черной масти, пойдите картой красной масти». Начинающим, особенно на первых порах, следует ограничиваться как можно более простыми правилами и лишь постепенно, по мере развития у них навыков игры переходить к более сложным. Тонкий замысел изобретателя элузиса наделил эту игру замечательной особенностью, которая заключается в том, что способ подсчета очков (который будет разъяснен дальше) заставляет сдающего с осторожностью подходить к выбору правила: оно должно быть не очень простым, иначе все его быстро разгадают, и в то же время не слишком сложным, чтобы кто-нибудь из играющих мог додуматься до него раньше других, не слишком затягивая игру. В этой особенности элузиса нетрудно усмотреть еще одну приятную аналогию: фундаментальные законы физики трудно открыть, но, коль скоро они уже открыты, их обычно можно записать в виде сравнительно простых уравнений.

После того как правило записано, начинается первый этап игры.

Первый играющий (из числа активных участников) берет любую из имеющихся у него карт и кладет ее вверх картинкой на первую карту исходного ряда. Если при этом задуманное правило не нарушается, то тот, кто сдавал карты, говорит: «Правильно», и карта остается в исходном ряду. Если же выложенная карта нарушает «сокровенное» правило, то сдававший карты произносит: «Неверно», тогда игрок, забрав свою карту, кладет ее перед собой вверх картинкой и очередь переходит к игроку, сидящему слева от только что ходившего. Каждый играющий по очереди имеет право выложить за один раз лишь одну карту. «Ошибочные» карты игроки раскладывают веером перед собой (вверх картинкой) так, чтобы каждый мог видеть свои карты. «Правильные» карты, образующие «исходный ряд», также раскладываются на столе для всеобщего обозрения. Типичный «исходный ряд» показан на рис. 154.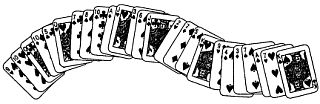

Рис. 154 Типичный «исходный ряд» при игре в элузис. Какому тайному правилу следует чередование карт?

Каждый игрок стремится проанализировать расположение карт в исходном ряду и открыть правило, определяющее чередование карт. Результат своих размышлений он формулирует в виде гипотезы и может проверить свою догадку, пойдя либо правильной (то есть согласующейся с принятой им гипотезой) картой, либо картой, которая, по его мнению, будет возвращена как ошибочная. Первая половина игры заканчивается после того, как каждый из участников проверит по одному разу все свои «ошибочные» карты.

Затем производится подсчет очков, набранных тем, кто сдавал карты. Заработанные им очки зависят от того, насколько ведущему (то есть набравшему наименьшее число «ошибочных» карт) игроку удалось вырваться вперед по сравнению с остальными игроками.

Если активных игроков двое, то сдававший карты получает число очков, равное разности между числом «ошибочных» карт у отстающего и у ведущего игроков. Если игроков (не считая того, кто раздавал карты) трое, то количество «ошибочных» карт у ведущего игрока нужно умножить на 2, а результат вычесть из общего числа ошибочных карт у двух остальных игроков. При игре вчетвером (тот, кто сдает карты, по-прежнему «в счет не идет») количество ошибочных карт у ведущего игрока умножить на 3, а то, что получится, вычесть из общего количества «ошибочных» карт у остальных игроков. Если играющих пятеро, то число ошибочных карт у ведущего игрока нужно умножить на 4; если их шесть — на 5 и т. д. Какие именно карты остались у игроков и какой масти, при подсчете очков роли не играет.

Предположим, например, что в элузис играют три человека и еще один сдает карты. Пусть у первого игрока осталось 10, у второго 5 и у третьего 3 карты. Дважды 3 равно 6. Следовательно, после вычитания 6 и 15 мы найдем, что тот, кто давал карты, набрал 9 очков.

Посчитав и записав число очков у «арбитра», переходят ко второму, заключительному этапу элузиса. Теперь уже в ход идут «ошибочные» карты.

Каждый игрок, как и прежде, раскладывает перед собой карты веером вверх картинкой (и может при этом их как угодно перетасовывать). Играют по очереди. Каждый игрок имеет право пойти любой картой. Тот, кто раздавал карты, комментирует сделанный ход, сообщая, правильно ли он был сделан или нет. Если ход был неверным, то играющий забирает свою карту назад и подыскивает ей замену среди оставшихся у него карт. Вторая половина игры заканчивается либо тогда, когда кто-нибудь из игроков сдаст все свои каюты, либо тогда, когда тот, кто сдавал карты, увидит, что задуманное им правило не позволяет продолжать игру.

После этого разворачивают листок бумаги и оглашают записанное там правило. Чтение правила в каком-то смысле соответствует заключительной стадии работы математика — дедуктивному доказательству теоремы, ранее нащупанной им индуктивно, на основе ряда частных наблюдений. Ученые, конечно, лишены возможности провести подобную окончательную проверку, им приходится довольствоваться лишь установлением большей или меньшей степени вероятности своих гипотез.

Вернемся теперь к подсчету очков, набранных игроками. Он производится почти так же, как подсчет очков у того, кто сдавал карты. Каждый игрок умножает число оставшихся у него карт на число остальных игроков (не считая того, кто сдавал карты) и вычитает произведение из общего числа карт, оставшихся у остальных игроков. Если в результате получается отрицательное число, то игроку засчитывается 0 очков. Вышедший из игры (то есть сдавший все свои карты) получает премию в 6 очков. Если из игры никто не вышел, то премию получает игрок с наименьшим количеством карт. Если таких игроков два или больше, то премия делится между ними поровну. Например, если в игре участвовало (имеются в виду лишь активные участники) четверо и у игроков осталось по 2, 3,10 и 0 карт, то это означает, что они набрали по 7, 3, 0 и 21 очку.

После подсчета очков право сдавать карты получает игрок, сидящий слева от предыдущего «арбитра». Игра продолжается до тех пор, пока каждый из игроков дважды не дождется своей очереди сдавать карты. Затем производится окончательный подсчет очков, и тот, кто набрал очков больше других, объявляется победителем партии.

Если задуманное правило применимо лишь к последовательности, состоящей по крайней мере из двух карт, то первая карта, какой бы она ни была, всегда будет правильной. В правилах, носящих числовой характер, туз следует считать единицей, валет — одиннадцатью, даму—двенадцатью, короля — тринадцатью. Если разрешается «зацикливаться» (то есть строить последовательность на циклических повторениях, например: валет — дама — король — туз — двойка — тройка —… — валет — дама —…), то это должно быть особо оговорено в правиле.

Следует избегать правил, ограничивающих выбор игрока менее чем | всех карт в колоде. Например, правило «Пойдите картой, следующей по старшинству за верхней картой в исходном ряду» неприемлемо, поскольку игрок может пойти лишь четырьмя из 52 карт.

Записав правило, «арбитр» при желании может немного подсказать остальным игрокам. Например, он может сообщить, что задуманное правило относится к двум верхним картам в исходном ряду или к масти карт. Подсказывать после того, как игра началась, разрешается лишь в дружеской компании, с согласия всех игроков.

Обычно загадывают следующие правила (мы приводит их в порядке возрастания сложности).

1. Если верхняя карта четная, пойдите нечетной картой, и наоборот.

2. Пойдите картой либо той же масти, либо того же достоинства, что и верхняя карта в исходном ряду (как в карточной игре под названием «Восьмерки»).

3. Если две верхние карты одного цвета, пойдите картой, значение которой заключено между тузом и семеркой. Если же две верхние карты различных цветов, то пойдите картой, значение которой заключено между семеркой и королем.

4. Если вторая карта сверху красного цвета, пойдите картой равного ей или старшего достоинства. Если вторая карта сверху черного цвета, пойдите картой равного ей или меньшего достоинства.

5. Разделите значение верхней карты на 4. Если остаток от деления равен 1, то пойдите любой картой пик; если 2 — любой картой червей; если 3 — бубен и если 0 — треф.

Вряд ли нужно говорить, что в том случае, если игроки хоть немного искушены в математике, правила игры могут быть гораздо сложнее. Тому, кто сдает карты, следует помнить, что количество получаемых им очков зависит от того, сумеет ли кто-нибудь из игроков разгадать правило раньше остальных. Поэтому сдающему карты необходимо с особой тщательностью оценивать возможности игроков.

Разрешается загадывать и такие правила, в которых используются какие-нибудь данные о самих игроках. (В этой связи достаточно вспомнить физика, вносящего своим измерительным прибором возмущение в наблюдаемое явление, или антрополога, изменяющего своим исследованием изучаемую культуру.) Например, вполне допустимо такое правило: «Если в фамилии игрока нечетное число букв, он должен идти картой другого цвета, чем верхняя карта исходного ряда. В противном случае игрок должен пойти картой того же цвета, что и верхняя карта». Однако со стороны загадывающего было бы нечестно, если бы он, записав столь хитроумное правило, не предупредил об этом игроков.

На рис. 154 изображен исходный ряд, выложенный по простому, не упоминавшемуся в этой главе правилу. Читатель может доставить себе удовольствие и, прежде чем заглянуть в ответ, поломать голову над разгадкой правила. Следует заметить, что цвета первых семи карт чередуются, а затем это чередование нарушается.

Так часто случается и в игре, и в истории науки: игроки нередко следуют правилу, не совпадающему с истинным, но упорно цепляются за свою догадку до тех пор, пока эксперимент не покажет, что подлинное правило проще, чем они ожидали, или что достигнутый успех был случайным.

* * *

Хотя индуктивные черты присущи самым различным играм, лишь в немногих из них эти черты носят достаточно глубокий характер, чтобы игру можно было назвать индуктивной. Я могу назвать лишь игру в «морской бой» (иногда называемую сальво), детскую игру в «виселицу», «балду» и тому подобные игры, связанные с отгадыванием слов, и комнатную игру, известную под названием «В дорогу». В последней игре водящий записывает на листке бумаги правило, которым определяется, какие вещи можно брать с собой в дорогу. После этого он говорит: «Я возьму с собой…» — и называет вещь, которую (согласно правилу) можно взять в дорогу.

Остальные участники по очереди спрашивают, нельзя ли им взять с собой тот или иной предмет, а водящий сообщает, разрешает ли правило брать этот предмет или нет. Победителем считается тот, кто сумеет первым отгадать правило. Правила могут быть и простыми и сложными. Вот пример довольно хитроумного правила: название предмета и фамилия того, кто берет его в дорогу, должны начинаться с одинаковой буквы.

[Интересная игра была выпущена в продажу во Франции. Ее очень легко сделать самому. Игра похожа на детский строительный набор и состоит из сделанных из дерева фигур (точнее, призм с малой высотой), треугольников, квадратов, прямоугольников и кружков. Каждая фигура бывает трех цветов — красного, желтого и зеленого. Кроме того, фигуры бывают большими и маленькими (вдвое меньшими), а также толстыми (высота ~ 1 см) и тонкими (~ 1/2 см). Всего в наборе, таким образом, имеется 4x3x2x2 = 48 фигур. В них играют, как в элузис, но можно (особенно для детей) придумать более простые игры. Простейшая из них: спрятать одну фигуру и попросить отгадать, глядя на оставшиеся фигуры, какая из них спрятана. Отгадывать нужно в минимальный срок. Можно играть, как в домино, приставляя фигуры, сходные по одному из признаков (например, к красному большому толстому треугольнику можно приставить красный маленький тонкий квадрат). Можно требовать совпадения двух признаков или даже трех (в этом случае проще говорить об отличии по одному из признаков).

Другая игра: водящий задумывает один или два признака. Отгадывающий, указывая на один из кубиков, спрашивает: «Такой?»

Водящий отвечает «да» или «нет». Надо отгадать задуманные признаки за минимальное число ходов.

Интересное задание для детей состоит в том, что рисуют три пересекающиеся области (можно положить три обруча хула-хупа).

Они образуют три попарно общие области, одну, общую всем трем, и три непересекающиеся. Требуется положить в одну из областей, например, зеленые фигуры, в другую тонкие, а в третью круги.

Как разложить все фигуры наиболее быстро (не перекладывая)?

Ответ: начать с общей области.

Можно придумать очень много разных задач и игр. Наконец, как в элузисе, ведущий может задумывать правила игры, а играющие должны их отгадывать.]

Я думаю, что существует еще много неисследованных возможностей для создания необычных индуктивных игр, например отгадывание узоров. Представьте себе квадратную коробку, которая может вместить 100 квадратных шашек. Пусть имеется 600 таких шашек, выкрашенных с одной стороны в различные цвета. Оборотная сторона всех шашек выкрашена в черный цвет. Не считая черного цвета, всего имеется шесть различных цветов, по 100 шашек каждого цвета. Ведущий втайне от остальных участников игры укладывает 100 шашек в коробку, образуя из них симметричный узор (узоры могут быть самыми разнообразными, от однотонного квадрата из 100 шашек одного и того же цвета до весьма запутанных и сложных). Коробку с шашками переворачивают, кладут вверх дном на стол и осторожно снимают. На столе остается квадрат из 100 шашек, обращенных черной «изнанкой» вверх. Игроки по очереди вынимают одну шашку, узнают, какого она цвета, и кладут ее на место (по-прежнему черной стороной вверх). Первый, кто сумеет правильно нарисовать весь узор, считается победителем. Свои узоры игроки рисуют так, чтобы другие не видели, и показывают наброски только водящему.

Играя в элузис, трудно удержаться от искушения назвать сдающего карты «всевышним», и игроки часто прибегают к теологической фразеологии. Так, когда подходит чей-то черед сдавать карты, говорят, что настала его «очередь быть богом». Если сдающий карты ошибается и вопреки собственному правилу ошибочно называет карту правильной, то об этом происшествии говорят как о «чуде».

Роберт Эбботт рассказывает, что однажды сдававший карты, видя, что никто не может отгадать задуманное им правило, указал на карту, лежащую перед одним из игроков, и заявил: «Пойдите этой картой». Игрок воспринял эту подсказку как «божественное откровение».

Ответы

Правило, определяющее последовательность карт в исходном ряду, изображенном на рис. 154, формулируется так: «Если верхняя карта ряда четная, то ходят трефы или бубны; если верхняя карта нечетная, то ходят червы или пики».

Возможны и другие правила. Например такое: «Пойдите любой картой, которая по достоинству отличается от верхней карты исходного ряда». Это правило проще, но, даже допустив, что оно верно, мы вряд ли сможем объяснить, как могло возникнуть более тесное упорядочение карт, подчиняющееся первому правилу. Ведь вполне может случиться так, что все игроки ошибочно приняли за истинное первое правило и действовали соответственно ему, причем никто ни разу не пошел картой, равной по достоинству верхней карте исходного ряда. Разумеется, в настоящей игре ошибочные карты позволяют строить дополнительные предположения и отбирать среди конкурирующих гипотез нужную.

Некоторым нравится придумывать очень сложные правила.

Один из возможных вариантов выглядит так. Во внимание принимаются только численные значения карт, причем значение туза считается равным 14. Циклические повторения в расположении карт не допускаются. Ходить можно картой, значение которой либо больше, либо меньше значения верхней карты исходного ряда.

Если очередной игрок продолжает либо увеличивать, либо уменьшать значение карт, то он должен увеличить шаг между значениями карт. Если дальнейшее увеличение шага невозможно, то шаг считается равным 1.

То обстоятельство, что одни и те же факты можно объяснить с помощью различных гипотез и что любую гипотезу можно «перелицевать» так, чтобы она соответствовала и новым, ранее противоречившим ей фактам, позволяет нам глубже понять важную особенность научного метода. Например, если мы пойдем восьмеркой бубен на восьмерку треф, то последнее правило можно спасти, добавив, что восьмерка бубен — единственная карта, которой можно пойти в любой момент. Многие научные гипотезы (например, птолемееву модель Вселенной) пытались спасти, загромождая их все большими и большими подробностями, чтобы хоть как-нибудь объяснить новые факты, прежде чем окончательно отказаться от них в пользу более простого объяснения.

Из всего сказанного возникают два глубоких вопроса философии науки: почему простейшая гипотеза является наилучшей? Чем определяется "простота"?

Примечания:

5

'American Mathematical Monthly, 64, 1957, p. 143.

52

В 52 листа.