Глава 23. ЧИСЛО φ-ЗОЛОТОЕ СЕЧЕНИЕ

Самым известным из всех иррациональных чисел, то есть чисел, десятичные разложения которых бесконечны и непериодичны, следует считать число π — отношение длины окружности к ее диаметру. Иррациональное число φ («фи») известно не столь широко, но оно выражает фундаментальное отношение, имеющее почти такой же универсальный характер, как и число тг. Сходство между числами π и φ этим не исчерпывается: подобно π, φ обладает свойством возникать в самых неожиданных местах (см., например, решение задачи о круглом пятне в гл. 28).

Геометрический смысл φ ясен из рис. 125. Отрезок прямой разделен на два отрезка А и В, которые, как говорят, образуют «золотое сечение» отрезка А + В: длина всего отрезка (А + В) находится в таком же отношении к длине отрезка А, как и длина отрезка А к длине отрезка В. Отношение каждой пары отрезков и равно числу φ. Если длина отрезка В равна 1, то значение φ нетрудно вычислить из уравнения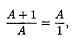

которое можно записать в виде обычного квадратного уравнения А² — А — 1 = 0. Положительный корень этого уравнения равен

Это число одновременно выражает длину отрезка А и значение величины φ. Его десятичное разложение имеет вид 1,61803398… Если за единицу принять длину А, то длина В будет выражаться величиной, обратной φ; то есть 1/φ. Любопытно, что 1/φ = 0,61803398.

Рис. 125 Золотое сечение: А относится к В так же, как А + В относится к А.

Число φ — единственное положительное число, которое переходит в обратное ему при вычитании единицы.

Подобно числу π, φ можно представить в виде суммы бесконечного ряда многими способами. Предельная простота следующих двух примеров еще раз подчеркивает фундаментальный характер φ:

Золотое сечение было известно древним грекам. Вряд ли можно сомневаться в том, что некоторые древнегреческие архитекторы и скульпторы сознательно использовали его в своих творениях. Примером может служить хотя бы Парфенон. Именно это обстоятельство и имел в виду американский математик Марк Барр, когда предложил называть отношение двух отрезков, образующих «золотое сечение», числом φ. Буква φ — первая греческая буква в имени великого Фидия, который, по преданию, часто использовал золотое сечение в своих скульптурах. Одной из причин, по которой пифагорейцы избрали пентаграмму, или пятиконечную звезду, символом своего тайного ордена, является то обстоятельство, что любой отрезок в этой фигуре находится в «золотом отношении» к наименьшему соседнему отрезку.

Многие математики, жившие в средние века и в эпоху Возрождения, были настолько увлечены исследованием необычайных свойств числа φ, что это походило на легкое помешательство. Примером тому могут служить слова Кеплера, которые Г. С. М. Коксетер приводит в качестве эпиграфа к главе о золотом сечении в своей книге «Введение в геометрию»:[42]

«Геометрия владеет двумя сокровищами: одно из них — теорема Пифагора, другое — деление отрезка в среднем и крайнем отношении. Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень».

В эпоху Возрождения отношение, выражаемое числом φ, называли «божественной пропорцией» или, следуя Евклиду, «средним и крайним отношением». Термин «золотое сечение» вошел в употребление лишь в девятнадцатом веке.

Много замечательных свойств числа φ, проявляющихся у различных плоских и пространственных фигур, было собрано в трактате Луки Пачоли, вышедшем в 1509 году под названием «De Divina Proportione» («О божественной пропорции») с иллюстрациями Леонадро да Винчи.[43] Число φ выражает, например, отношение радиуса окружности к стороне правильного вписанного десятиугольника.

Расположив три золотых прямоугольника (то есть прямоугольники, стороны которых находятся в «золотом отношении») так, чтобы каждый симметрично пересекался с двумя другими (под прямым углом к каждому из них), мы увидим, что вершины «золотых» прямоугольников совпадают с 12-ю вершинами правильного икосаэдра и в то же время указывают положение центров 12-и граней правильного додекаэдра (рис. 126 и 127).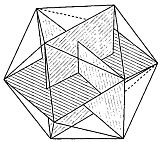

Рис. 126 Вершины «золотых» прямоугольников совпадают с вершинами икосаэдра.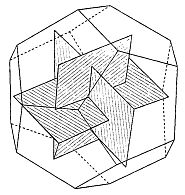

Рис. 127 Вершины тех же «золотых» прямоугольников, что и на рис. 126, совпадают с центрами граней додекаэдра.

Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники (рис. 128).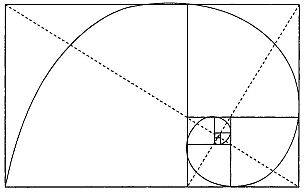

Рис. 128 Логарифмическая спираль, образованная «вращающимися квадратами».

(Тем самым будет построен пример совершенного квадрируемого прямоугольника бесконечного порядка. Подробно о квадрируемых прямоугольниках рассказывается в главе 32.) Точки, делящие стороны прямоугольников в среднем и крайнем отношении, лежат на логарифмической спирали, закручивающейся внутрь. Полюс спирали лежит на пересечении пунктирных диагоналей. Разумеется, «вращающиеся квадраты», как их принято называть, могут не только закручивать, но и раскручивать спираль. Для этого лишь требуется строить не уменьшающиеся, а все увеличивающиеся квадраты.

Логарифмическая спираль возникает и во многих других геометрических построениях, связанных с числом φ. Один из изящных способов вычерчивания логарифмической спирали основан на использовании равнобедренного треугольника, стороны которого находятся в золотом отношении к основанию (рис. 129).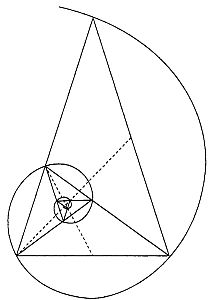

Рис. 129 Логарифмическая спираль, образованная «вращающимися треугольниками».

Углы при основании такого треугольника равны 72°, что вдвое больше угла при вершине, равного 36°. Именно из таких золотых треугольников построена пентаграмма. Точка пересечения биссектрисы угла при основании с противолежащей стороной делит эту сторону в среднем и крайнем отношении, при этом весь треугольник разбивается на два меньших треугольника, один из которых подобен исходному. В свою очередь этот треугольник также можно разбить на два еще меньших треугольника, проведя в нем биссектрису угла при основании, и т. д. Продолжая неограниченно этот процесс, мы получим бесконечную последовательность вращающихся треугольников, чьи вершины, так же как и вершины вращающихся квадратов, описывают логарифмическую спираль. Полюс этой спирали лежит на пересечении двух медиан, проведенных пунктиром.

Логарифмическая спираль — единственный тип спирали, не меняющей своей формы при увеличении размеров. Это свойство объясняет, почему логарифмическая спираль так часто встречается в природе. Например, по мере роста моллюска Nautilus раковина его, разделенная внутренними перегородками, увеличивается в своих размерах, закручиваясь по логарифмической спирали. При этом домик его не меняет формы: если центральную часть раковины посмотреть под микроскопом, мы увидим в точности такую же спираль, какая получилась бы, если бы раковина выросла до размеров галактики и мы разглядывали бы ее с большого расстояния.

Логарифмическая спираль тесно связана с числами Фибоначчи (1, 1, 2, 3, 5, 8, 13, 21, 34…; каждое последующее число, начиная с третьего, равно сумме двух предыдущих). Числа Фибоначчи часто встречаются в живой природе. Обычно в качестве примера приводят расположение листьев на черенке, лепестков некоторых цветков и семян в плодах. И здесь дело не обходится без числа φ, поскольку отношение двух последовательных членов ряда Фибоначчи тем ближе к числу φ, чем дальше мы продвинемся от начала ряда.

Так, 5/3 уже дает хорошее приближение к φ (прямоугольник с отношением сторон 5:3 трудно отличить от золотого прямоугольника), еще лучшее приближение дает 8/5, но его превосходит отношение 21/13, равное 1,615. Это свойство присуще не только числам Фибоначчи.

Начав с любых двух чисел и построив аддитивный ряд, в котором каждый член равен сумме двух предыдущих (например, ряд 7, 2, 9, 11, 20…), мы обнаружили, что отношение двух последовательных членов такого ряда также стремится к числу φ: чем дальше мы будем продвигаться от начала ряда, тем лучше будет приближение.

Это нетрудно понять, если воспользоваться вращающимися квадратами. Начнем с двух небольших квадратов любых размеров, например с квадратов А и В на рис. 130.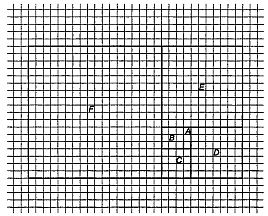

Рис. 130 Квадраты, показывающие, что отношение последующего члена любого аддитивного ряда к предыдущему стремится к числу φ.

Сторона квадрата С равна сумме сторон квадратов А и В; сторона квадрата D равна сумме сторон квадратов В и С; сторона квадрата Е — сумме сторон квадратов С и D и т. д. Независимо от длин сторон двух первых квадратов вращающиеся квадраты образуют прямоугольник, который все меньше и меньше отличается от золотого.

Тесную связь между числом φ и числами Фибоначчи наглядно демонстрирует классический геометрический парадокс. Если на бумаге в клеточку начертить квадрат 8 х 8 и разрезать его на 4 части так, как показано на рис. 131, то из этих частей можно составить прямоугольник, площадь которого равна 65 единичным клеткам, а не 64, как у исходного квадрата.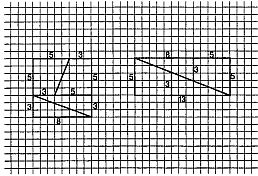

Рис. 131 Парадокс, основанный на свойствах произвольного аддитивного ряда.

Парадокс объясняется просто: части квадрата неплотно примыкают друг к другу вдоль диагонали и между ними остается узкий зазор. Его площадь равна «лишней» клетке. Заметим, что длины сторон трапеций и треугольников, на которые разрезали квадрат, выражаются числами Фибоначчи. На самом деле парадокс будет возникать и в том случае, если квадрат разрезан на трапеции и треугольники, длины которых выражаются членами любого аддитивного ряда, хотя при этом в одних случаях построенный из частей квадрата прямоугольник будет иметь бблыную, а в других — меньшую площадь по сравнению с квадратом в зависимости от того, как примыкают части вдоль диагонали: есть ли между ними зазор или они перекрываются. Это обстоятельство связано с тем, что отношение последующего члена аддитивного ряда к предыдущему то превосходит φ, то становится меньше этого числа.

Площадь прямоугольника, составленного из частей разрезанного квадрата, в точности совпадает с площадью квадрата лишь в одном случае: если длины сторон трапеций и треугольников взяты из членов аддитивного ряда 1, φ, φ+1, 2φ+1, 3φ + 2… (другой — «мультипликативный» — способ записи того же ряда выглядит так: 1, φ, φ², φ³, φ⁴….). Это единственный аддитивный ряд, в котором отношение любых двух последовательных членов постоянно (и, конечно, равно φ). Это тот самый «золотой» ряд, которым тщетно стремятся стать все аддитивные ряды.

Обширная литература, посвященная числу φ и связанным с ним вопросам, не менее эксцентрична, чем литература о квадратуре круга, так или иначе затрагивающая свойства другого иррационального числа — π. [Добавим несколько замечаний, взятых из книги Н. von Baravalle «Geometrie als Sprache der Formen».

Связь φ с числом Фибоначчи иллюстрируется лучше всего таким образом. Если взять разложение 1/φ в цепную дробь

и построить «подходящие дроби», откидывая «хвосты», то можно получить ряд чисел:

Продолжая в том же духе, получим ряд подходящих дробей:

В этом ряду каждый знаменатель становится числителем у следующей дроби. Числители и знаменатели образуют ряд Фибоначчи:

Так как приближение к 1/φ можно начинать с любых двух чисел, то читатель сразу увидит разгадку следующего фокуса.

Попросите двух человек написать на длинной бумажке два любых числа одно под другим, а третьего — подсчитать и записать их сумму. Перегните бумажку, оставив видными только два последних числа, и опять попросите написать их сумму; опять перегните бумажку и повторите просьбу сложить два числа. Повторив эту операцию раз 10–15, попросите разделить предпоследнее число на последнее (с точностью, скажем, до трех знаков). Результат вы можете предсказать заранее: он будет 0,618!

Наконец, составим последовательность равенств:

И здесь коэффициенты — члены ряда Фибоначчи!]

Классическим примером может служить объемистый (457 страниц) труд Адольфа Цейзинга «Der goldene Schnitt» («Золотое сечение»), опубликованный в 1881 году. Цейзинг доказывает, что из всех пропорций именно золотое сечение дает наибольший художественный эффект и доставляет наибольшее удовольствие при восприятии. Именно в золотом сечении, по Цейзингу, кроется ключ к пониманию всей морфологии (в том числе строения человеческого тела), искусства, архитектуры и даже музыки. В том же духе выдержаны и книги «Nature's Harmonic Unity» («Гармоническое единство природы») С. Колмена A913) и «The Curves of Life» («Кривые жизни») Т. Кука A914).

Вряд ли будет преувеличением сказать, что экспериментальная эстетика берет свое начало с попыток Густава Фехнера эмпирически обосновать взгляды Цейзинга. Немецкий физиолог измерил отношения сторон у тысяч окон, картинных рам, игральных карт, книг и других прямоугольных предметов, проверил, в каком отношении поперечные перекладины могильных крестов на кладбищах делят вертикальные планки, и обнаружил, что в большинстве случаев полученные им числа мало отличаются от φ. Фехнер разработал целый ряд остроумных тестов, в которых испытуемому предлагалось выбрать «милый его сердцу» прямоугольник из большого набора прямоугольников с различным соотношением сторон, нарисовать самый «приятный» многоугольник, провести поперечную линию и превратить вертикальную палочку в крест, выбрав место пересечения перекладин по своему усмотрению, и т. д. И здесь многократно проведенные опыты показали, что испытуемые отдают предпочтение отношениям, близким к числу φ. Разумеется, основополагающие работы Фехнера были грубы, и более поздние исследования, проводимые в аналогичном направлении, позволяли прийти лишь к более расплывчатому утверждению о том, что большинство людей отдают предпочтение прямоугольнику, занимающему промежуточное положение где-то между квадратом и прямоугольником, у которого основание вдвое больше высоты.

Американец Джей Хэмбридж, скончавшийся в 1924 году, написал много книг, в которых отстаивал понятие «динамической симметрии», понимая под этим применение геометрии (ведущей роли числа φ в искусстве, архитектуре, проектировании мебели и даже типографских шрифтах. В наши дни мало кто принимает его работы всерьез, хотя время от времени какой-нибудь знаменитый художник или архитектор так или иначе использует золотое сечение.

Например, Джордж Беллоуз иногда брал золотое сечение за основу композиции своих картин. Холст, на котором написана «Тайная вечеря» Сальвадора Дали, имеет форму золотого прямоугольника.

Золотые прямоугольники меньших размеров использованы художником при размещении фигур двенадцати апостолов. Над столом как бы плавают в воздухе части огромного додекаэдра.

Много размышлял на тему о числе φ Фрэнк А. Лонк. Его брошюры обычно издавало фортеановское общество Т. Тэйера. Кстати сказать, это же общество выпустило и логарифмическую линейку, на которой среди прочих замечательных констант было нанесено число φ (общество прекратило свое существование в 1959 году, после смерти Тэйера). Лонк подтвердил одну из любимых теорий Цейзинга, измерив рост 65 женщин и сравнив полученные данные с расстоянием от пупка соответствующей особы до пола. Среднее значение этого отношения оказалось равным 1,618… и было названо автором «относительной постоянной Лонка». «Субъекты, у которых отношение данных измерения не совпадало с указанной постоянной, — писал Лонк, — при опросе неизменно сообщали о том, что перенесли в детстве вывих бедра или стали жертвой несчастного случая, повлекшего за собой деформацию тела». Лонк оспаривал широко распространенное мнение о том, что десятичное разложение числа π имеет вид 3,14159…. Он произвел более точные вычисления, возведя в квадрат число φ, умножив результат на 6 и поделив затем полученное число на 5. По его подсчетам, значение π выражается десятичным числом 3,14164078644620550.

В заключение этой главы я приведу интересную задачу, связанную с числом φ и эмблемой «Свободной Франции» (организации, которую в годы второй мировой войны возглавлял генерал де Голль) — лотарингским крестом, изображенным на рис. 133.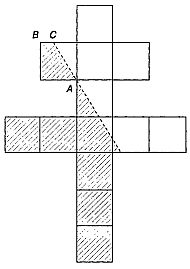

Рис. 133 Лотарингский крест. Чему равна длина отрезка ВС?

Крест этот составлен из 13 единичных квадратов. Задача состоит в следующем: через точку А нужно провести прямую так, чтобы площадь заштрихованной части креста была равна площади той его части, которая лежит по другую сторону прямой. Чему равна длина отрезка ВС, если считать, что прямая проведена правильно (на рис. 133 умышленно показано неверное положение прямой, чтобы читатель, взглянув на чертеж, не мог отгадать истинное решение).

* * *

Много интересных писем пришло в редакцию Scientific American в связи со статьей о числе φ. Читатели обращали внимание на то, что в большинстве математических книг и журналов отношение длин отрезков, образующих золотое сечение суммарного отрезка, принято обозначать не буквой φ, а другой греческой буквой — τ («тау»). Это действительно так, но во многих нематематических книгах то же отношение обозначено буквой φ, и именно этот символ чаще всего встречается в занимательной литературе.

Один из читателей для вычисления числа φ с точность до 2878 десятичных знаков воспользовался компьютером. На всю работу компьютеру понадобилось меньше четырех минут. Для любителей числовых курьезов сообщаем, что среди первых 500 цифр встречается необычная последовательность 177111777.

Другой читатель сообщил, что отношение длин пунктирных диагоналей на рис. 128 и пунктирных медиан на рис. 129 равно числу φ.

Стифен Барр, сын Марка Барра, давшего числу φ его название, прислал мне оттиск статьи своего отца, опубликованной в лондонском Sketch в 1913 году. В этой статье содержится следующее обобщение этого замечательного числа. Если построить аддитивный ряд, в котором каждый член (начиная с четвертого) равен сумме трех предыдущих, то предел отношения последующего члена ряда к предыдущему будет равен 1,8395… Аналогичный предел для аддитивного ряда, в котором каждый член, начиная с пятого, равен сумме четырех предыдущих, равен 1,9275…. В общем случае

где n — число слагаемых, которые необходимо взять для получения следующего члена ряда, а х — предел отношения последующего члена ряда к предыдущему. При n = 2 мы получаем обычные числа Фибоначчи с х = φ. При n, стремящемся к бесконечности, х стремится к 2.

Теория Цейзинга относительно расстояний от пупка до пола время от времени встречается и в современных книгах. Например, в книге Матила Гика[44] мы читаем: «Можно с уверенностью утверждать, что, измерив указанное отношение для большого числа мужчин и женщин, мы в среднем получим для него значение 1,618».

Смысл этого утверждения столь же неясен, сколь и смысл утверждения о вычислении «среднего отношения длины клюва птицы к длине ее ноги». По какой группе людей следует производить усреднение: по случайным образом выбранным жителям Нью-Йорка, Шанхая или по случайной выборке из населения всего земного шара? Положение усугубляется тем, что во всем мире и даже в небольших районах земного шара наблюдается сильное смешение типов телосложения.

Двое друзей из Сиэтла произвели соответствующие измерения над своими женами и получили отношение, равное 1,667, что несколько больше приводимого Лонгом значения 1,618. «Мы особо подчеркиваем, — пишут они, — что обмер наших «высокопараметрических» жен производили их уважаемые мужья. Нам кажется, что мистеру Лонку лучше всего оставить архитектуру пупков и заняться чем-нибудь другим».

Ответ

Задачу о разбиении лотарингского креста на две равновеликие части можно решать алгебраически. Обозначим через х длину отрезка CD (рис. 134) и через у — длину отрезка MN.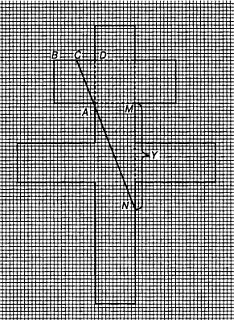

Рис. 134 Решение задачи с лотарингским крестом.

Если проведенная линия делит крест на две равновеликие части, то площадь заштрихованного треугольника должна быть равной 2,5 квадратной единицы. Это позволяет записать уравнение: (х + 1)(у + 1) = 5. Поскольку треугольники ACD и AMN подобны, мы можем составить второе уравнение: x/1 = 1/y

Решая систему двух полученных уравнений, находим

Следовательно, длина отрезка ВС равна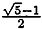

или 0,618…, то есть 1/φ. Иначе говоря, отрезки ВС и CD образуют золотое сечение отрезка BD. Точно так же нижний конец диагональной прямой делит сторону единичного квадрата на отрезки, образующие ее золотое сечение. Длина прямой, делящей лотарингский крест на две равновеликие части, равна, таким образом,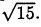

Для того чтобы найти положение точки С с помощью циркуля и линейки, можно воспользоваться любым из нескольких простых методов, восходящих к Евклиду. Один из них заключается в следующем.

Проведем прямую BE так, как показано на рис. 135.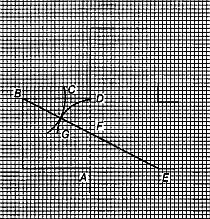

Рис. 135 К решению задачи с лотарингским крестом.

Эта прямая делит отрезок AD пополам, так что DF = BD/2. С помощью циркуля проведем дугу окружности с центром в точке F и радиусом DF. Эта дуга пересекает отрезок BF в точке G. С центром в точке В проведем дугу окружности радиусом BG, пересекающую BD в точке С. Это и дает искомое золотое сечение отрезка BD.

Некоторые читатели нашли более простые способы решения задачи. Вот одно из самых простых построений прямой, делящей лотарингский крест на две равновеликие части: полуокружность, один конец которой проходит через точку А (рис. 134), а другой — через точку, расположенную на три единицы ниже на одной вертикали с А, пересекает правую границу креста в точке N.

Примечания:

4

То frustrate — расстраивать, делать что-либо тщетным, безнадежным, обрекать на неудачу (англ.).

42

Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966.

43

Pacioli L. De Divina Proportione. — Milan: 1956.

44

Ghyka M. The Geometry of Art and Life. — Sheed and Ward, 1946.