Глава 13. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ

Математический парадокс можно определить как истину, настолько противоречащую нашему опыту, интуиции и здравому смыслу, что в нее трудно поверить даже после того, как мы шаг за шагом проследим все ее доказательство. Математическим софизмом принято называть не менее удивительные утверждения, в доказательствах которых в отличие от доказательства парадоксов кроются незаметные, а подчас и довольно тонкие ошибки. В любой области математики — от простой арифметики до современной теоретико-множественной топологии — есть свои псевдодоказательства, свои софизмы. В лучших из них рассуждения с тщательно замаскированной ошибкой позволяют приходить к самым невероятным заключениям. Ошибкам в геометрических доказательствах Евклид посвятил целую книгу, но до наших дней она не дошла, и нам остается лишь гадать о том, какую невосполнимую утрату понесла из-за этого элементарная математика.

Семь математических софизмов, о которых пойдет речь в этой главе, выбраны из разных областей математики, каждый из них по-своему интересен. Объяснять, в чем состоит ошибочность рассуждения в каждом софизме, мы не будем, чтобы не лишать читателя удовольствия самостоятельно найти ее.

Наш первый софизм чрезвычайно элементарен. Мы предпошлем ему занимательный парадокс, на примере которого великий немецкий математик Давид Гильберт любил объяснять необычные свойства наименьшего из трансфинитных чисел «алеф-нуль». Как-то раз хозяину одной великолепной гостиницы с бесконечным, но счетным числом номеров, ни один из которых не был свободен, нужно было принять нового гостя. Хозяин вышел из положения очень просто: каждого из своих постояльцев он переселил в комнату, номер которой был на единицу больше номера прежней комнаты, в результате чего обитатель n-й комнаты переехал в (n + 1) — ю и освободил для нового гостя самую первую комнату. Как может поступить хозяин, если прибудет бесконечное множество новых гостей?

Ничуть не смущаясь, хозяин переселяет всех своих прежних постояльцев в комнаты с вдвое большими номерами (гость из комнаты 1 переезжает в комнату 2, гость из комнаты 2 — в комнату 4, гость из комнаты 3 —в комнату 6, гость из комнаты 4 — в комнату 8 и т. д.) и размещает вновь прибывших в освободившихся комнатах с нечетными номерами.

Но так ли необходимо хозяину иметь счетное число комнат для того, чтобы разместить новых гостей? В приведенных ниже стишках, взятых из одного английского журнала, выходившего в прошлом веке, рассказывается о хитром хозяине гостиницы, сумевшем разместить в девяти номерах десять гостей так, что каждому из них досталось по отдельной комнате.

Их было десять чудаков,
Тех спутников усталых,
Что в дверь решили постучать
Таверны «Славный малый».
— Пусти, хозяин, ночевать,
Не будешь ты в убытке,
Нам только ночку переспать,
Промокли мы до нитки.
Хозяин тем гостям был рад,
Да вот беда некстати:
Лишь девять комнат у него
И девять лишь кроватей.
— Восьми гостям я предложу
Постели честь по чести,
А двум придется ночь проспать
В одной кровати вместе.
Лишь он сказал, и сразу крик,
От гнева красны лица:
Никто из всех десятерых
Не хочет потесниться.
Как охладить страстей тех пыл,
Умерить те волненья?
Но старый плут хозяин был
И разрешил сомненья.
Двух первых путников пока,
Чтоб не судили строго,
Просил пройти он в номер «А»
И подождать немного.
Спал третий в «Б», четвертый в «В»,
В «Г» спал всю ночь наш пятый,
В «Д», «Е», «Ж», «3» нашли ночлег
С шестого по девятый.
Потом, вернувшись снова в «А»,
Где ждали его двое,
Он ключ от «И» вручить был рад
Десятому герою.
Хоть много лет с тех пор прошло,
Неясно никому,
Как смог хозяин разместить
Гостей по одному.
Иль арифметика стара,
Иль чудо перед нами,
Понять, что, как и почему,
Вы постарайтесь сами.

Примером более тонкого математического софизма служит следующее «алгебраическое» доказательство того, что любое число аравно меньшему числу b.

Начнем с равенства

а = b + с.

Умножив обе его части на а — b, получим

а2 — ab = ab + ac — b2 — be.

Перенесем ас в левую часть:

а2 — ab — ас = ab — b2 — be

и разложим на множители:

а(а — b — с) = b(а — b — с).

Разделив обе части равенства на а — b — с, найдем

а = b,

что и требовалось доказать.

Много неприятностей подстерегает того, кто неосторожно обращается с мнимой единицей i (квадратным корнем из -1). Об этом свидетельствует хотя бы следующее удивительное «доказательство» равенства 1 = — 1:

В планиметрии большая часть ошибочных доказательств связана с использованием неправильных чертежей. Рассмотрим, например, удивительное «доказательство» того, что площадь лицевой стороны многоугольника, вырезанного из бумаги, отличается от площади оборотной стороны того же многоугольника. Это «доказательство» придумано врачом-психиатром Л. Восбургом Лионсом, в нем используется один любопытный принцип, открытый П. Керри.

Прежде всего начертим на листке бумаги в клетку треугольник, площадь которого равна 60 клеткам (рис. 82), и разрежем его вдоль прямых, показанных на верхнем рисунке.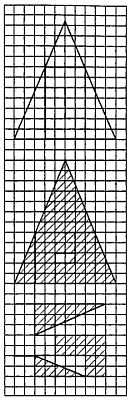

Рис. 82 Треугольник Керри.

Перевернув части треугольника на другую сторону и составив из них треугольник, изображенный на рис. 82 в середине, мы обнаружим, что в центре нового треугольника появилась дырка площадью в 2 клетки.

Иначе говоря, суммарная площадь частей исходного треугольника при переворачивании уменьшилась до 58 клеток! Перевернув еще раз (лицевой стороной вверх) лишь три части исходного треугольника, мы сможем составить из всех шести частей фигуру, изображенную на рис. 82 внизу. Ее площадь равна 59 клеткам. Что-то здесь не так, это ясно, но что именно?

Теория вероятностей изобилует правдоподобными, но логически не безупречными рассуждениями. Предположим, что вы встретились со своим другом Джоном и что каждый из вас носит тот галстук, который ваша жена подарила ему на Рождество. Вы начинаете спорить о том, чей галстук дороже, и в конце концов решаете пойти в магазин, где были куплены галстуки, и узнать, сколько стоит каждый из них. Тот, кто выиграет (чей галстук окажется дороже), по условию пари должен отдать свой галстук проигравшему, чтобы смягчить горечь поражения.

Вы рассуждаете так: «Шансы выиграть и проиграть у меня одинаковые. Выиграв, я обеднею на сумму, равную стоимости моего галстука. Проиграв, я получу более дорогой галстук. Следовательно, заключив пари, я окажусь в более выгодном положении, чем мой приятель».

Разумеется, ничто не мешает Джону рассуждать точно так же.

Могут ли обе стороны, заключившие пари, иметь преимущество друг перед другом?

Один из наиболее впечатляющих парадоксов топологии заключается в том, что тор (поверхность бублика), если его поверхность растягивать (не разрывая при этом), можно вывернуть наизнанку через любую сколь угодно малую дырочку. Никакой проблемы здесь нет. Но уж если тор действительно можно вывернуть наизнанку, то следует обратить внимание и еще на один, пожалуй, даже более замечательный факт.

На наружной стороне тора проведем меридиан (рис. 83, ввер-вверху). На внутренней стороне того же тора проведем параллель.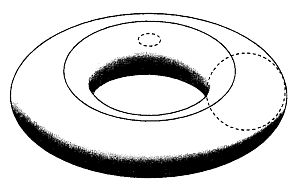

Рис. 83 Если тор вывернуть наизнанку, то кажется, что кольца, нарисованные на его поверхности, расцепляются.

Обе эти окружности, очевидно, сцеплены между собой. Вывернем теперь тор наизнанку через дырочку в его поверхности. Как видно из нижнего рисунка, первая окружность перейдет с наружной поверхности тора внутрь, а вторая — наружу, и обе окружности окажутся расцепленными! Очевидно, что это нарушает фундаментальный топологический закон, который гласит: разделить две сцепленные замкнутые кривые можно, лишь разорвав одну из кривых и протащив через место разрыва вторую.

В нашем последнем софизме, заимствованном из элементарной теории чисел, речь пойдет о сравнительных достоинствах «интересных» чисел. Разумеется, числа могут представлять интерес с различных точек зрения. Так, для Джорджа Мура, когда он писал свою знаменитую оду тридцатилетней женщине, особый интерес представляло число 30 — Мур считал, что в этом возрасте замужние женщины особенно привлекательны. Для специалиста по теории чисел число 30 представляет, по-видимому, еще больший интерес, поскольку это наибольшее из чисел, обладающих тем свойством, что все меньшие числа, не имеющие с ними общих делителей, просты. Число 15 873 также небезынтересно: если его умножить сначала на любую цифру, то есть на любое из чисел от 1 до 9, а затем на 7, то результат будет состоять из повторений выбранной для первого умножения цифры. Еще более удивительными свойствами обладает число 142 857: умножая его на числа от 1 до 6, вы будете получать циклические перестановки одних и тех же шести цифр.

Возникает вопрос: существуют ли неинтересные числа? С помощью элементарных рассуждений нетрудно доказать, что неинтересных чисел нет. Если бы скучные числа существовали, то все числа можно было бы разбить на два класса: интересные числа и неинтересные, скучные числа. Во множестве неинтересных чисел нашлось бы одно число, которое было бы наименьшим из всех неинтересных чисел. Но наименьшее из всех неинтересных чисел — это уже число само по себе интересное. Поэтому мы должны были бы изъять его из множества неинтересных чисел и перевести в другое множество.

В оставшемся множестве в свою очередь нашлось бы наименьшее число. Повторяя этот процесс достаточно долго, можно сделать интересным любое неинтересное число.

* * *

Наибольшее беспокойство читателям доставил софизм с вывернутым наизнанку тором. Тор действительно можно вывернуть наизнанку, но это изменяет его ориентацию. В результате обе окружности меняются местами и остаются в зацеплении. Если отрезать нижнюю часть чулка и сшить концы в трубку, получится превосходная модель тора. На ней нитками различных цветов можно простегать меридиан и параллель. Такой тор легко вывернуть через дырочку в поверхности, при этом прекрасно видно все, что происходит с меридианом и параллелью.

Подробное объяснение софизма с треугольником и некоторые другие головоломки можно найти в двух главах «Исчезновение фигур» моей книги «Математические чудеса и тайны».[25] Софизм с галстуком подробно разобран у М. Крайчика.[26]

Заключительное «доказательство» того, что неинтересных чисел не существует, вызвало следующую телеграмму читателя:

Немедленно прекратите вылавливать неинтересные числа и превращать их в интересные. Для интереса оставьте хоть одно неинтересное число!

Примечания:

2

Schaat W. L. Recreational Mathematics, 3d rev. ed. — 1963.

25

Гарднер М. Математические чудеса и тайны. — М.: Наука, 1964.

26

Kraitchik M. Mathematical Recreations. — 1942.