Развитие отдельных направлений программирования, филологии, психологии, теории проектирования и искусственного интеллекта подошло к точке, когда ощущается настоятельная необходимость интеграции накопленных результатов. Попытка такой интеграции воплотилась в излагаемой далее проектной процедуре (методике), которая может быть применена для составления функциональных описаний (структурированных описаний процессов). Инструкция пользования каким-либо устройством, инструкция вообще или алгоритм программы являются описаниями функционирования. Описания функционирования могут быть как структурированными в соответствии с излагаемым подходом к структурированию, так и неструктурированными. Таким образом, в данной главе рассматривается именно проектная процедура (методика) разработки функциональных описаний функционирования систем, отличающаяся использованием особого структурирования.

Программисты могут применять проектную процедуру при написании:

— документальных описаний вычислительных и иных алгоритмов, предназначенных для тиражирования;

— инструкций работы пользователя в системе организации (учреждения) с использованием ЭВМ и разрабатываемой программы;

— описаний внешнего функционирования программы в форме сценария работы программы (такие описания предшествуют внутреннему проектированию программы);

— внутренних спецификаций функционирования программы (метода решения задачи, алгоритма программы в целом);

— исходных текстов модулей программы при использовании технологии структурного программирования;

— кода методов объектов при использовании технологии объектно-ориентированного программирования;

— текстов помощи по использованию программы.

Умение применять проектную процедуру полезно и непрограммистам. При помощи данной проектной процедуры можно составлять:

• короткие и понятные описания любых процессов;

• приказы и распоряжения на выполнение работ;

• инструкции пользования изделиями;

• описания принципов функционирования изделий;

• описания бизнес-процессов;

• бухгалтерские инструкции по проведению расчетов;

• тексты должностных инструкций организационного обеспечения.

Данный список не является исчерпывающим и возможны все новые применения.

Более подробно актуальность разработки функциональных описаний вне сферы программирования характеризуется следующими примерами.

"Копать траншею от забора до обеда" — неудачное распоряжение (недостаточно полно выявлена и указана входная и выходная информация, а также отсутствует цель).

Предположим, что в конце июня некий отечественный бухгалтер обратился с просьбой об отпуске. Главный бухгалтер, вероятнее всего, даст примерно такой ответ: "Не дам никакого отпуска до сдачи полугодового отчета". Представим себе, что имеется набор ежедневных детально исчерпывающих инструкций по работе данного бухгалтера. Набор таких инструкций называется описанием бизнес-процессов. В этом случае да и в случае болезни работа бухгалтера передается резервному специалисту. Предположим, что сверху спущен какой-то документ, согласно которому надо представить какие-то ранее не рассчитываемые данные. Скорее всего, данный документ представляет собой запутанную инструкцию, допускающую разночтение или даже содержащую ошибки для применения в некоторых особых случаях. Источником таких ошибок может являться не злой умысел составителя инструкции, а неспособность ее составителя охватить все особые случаи в силу огромного (астрономического!) количества путей выполнения инструкции, разработанной по традиционной операционной методике. Теперь главный бухгалтер начинает обзванивать коллег и инстанции в надежде получить разъяснения. Пусть он разобрался в инструкции. Теперь перед ним встает задача по отдаче распоряжений работникам бухгалтерии как работать при изменившихся условиях. Многие бухгалтеры, не зная основ современной алгоритмизации, скорее всего, обратятся к хорошо оплачиваемым программистам для избежания затруднений в отдаче распоряжений.

В отличие от бухгалтера, документально фиксирующего все свои действия, прораб на стройке свои распоряжения по производству работ готовит и отдает устно. Это объясняется традиционным уходом от ответственности в случае травматизма рабочих. Устная подготовка распоряжений приводит к таким ошибкам, как что-то не удается разместить в уже построенной части здания. Таким образом, строительство ведется циклическим процессом: строить — ломать — строить и т. д., что ведет к удорожанию строительства.

Продажа и даже перепродажа готовых технических изделий по действующему законодательству предполагает наличие инструкции пользования изделия на русском языке. Однако часто оказывается, что инженеры составляют такие длинные и запутанные инструкции пользования объектами техники, что потребители начинают эксплуатацию изделия с недопустимых действий, которые могут привести изделие даже к неремонтно-пригодному состоянию.

Помимо апробации в области программирования авторы учебника провели апробацию изложенных в нем методик при обучении непрограммирующих специальностей. Оказалось, что обучение методике разработки функциональных описаний (на примерах составления инструкций вообще, описаний бизнес-процессов) вполне доступно студентам второго курса специальности бухгалтерский учет, даже если они не изучали эту методику в курсе программирования. Более того, половина учеников девятого класса обычной школы вполне способна полностью освоить данный материал. Следует отметить такой факт: до обучения лишь несколько учеников класса реально могли написать план, а потом сочинение. После обучения практически три четверти обучаемых могли написать план, а затем его развить в сочинение, т. е. школьники реально освоили элементы дедуктивного мышления! Затраты на освоение материала составили 8 ч лекционных и 16 ч практических занятий. Таким образом, у обучаемых всего за 24 ч учебных занятий удается развить первичные навыки дедуктивного мышления и владение начальными методами системного подхода.

Написание технической документации — особый жанр писательского искусства. В настоящее время в развитых странах появляется новая специальность Technical Writer — технический писатель. Вероятно, одна из сфер применения проектной процедуры заключается в ее использовании такими специалистами.

Хорошим функциональным описанием является описание безошибочное, однозначное для читателя, краткое, суть которого понимается быстро. Согласно проектной процедуре хорошее функциональное описание составляется от общего к частному с использованием особых конструкций предложений — типовых элементов (типовых структур или просто структур), составляющих семантический скелет будущих инструкций.

Обычно человек мыслит предложениями естественного языка. Если научиться упорядочивать мысли в процессе мышления, то можно научиться получать алгоритмы и иные функциональные описания со скоростью не только не меньшей, чем до обучения, но даже большей. Опытный программист пишет текст на языке программирования со скоростью, с которой он думает, а в случае простых алгоритмов — со скоростью набора текста на клавиатуре. Инструкции, предназначенные для исполнения людьми, могут содержать как алгоритмы, так и эвроритмы.

Одно из преимуществ применения проектной процедуры заключается в снижении умственной усталости программиста или составителя инструкций за счет исключения необходимости неоднократного повторения мыслительного процесса для получения одной и той же забываемой идеи.

Главное преимущество состоит в однозначности соответствия функционального описания замыслу, что достигается исчерпывающим тестированием. При операционном подходе к составлению описаний функционирования исчерпывающее тестирование принципиально невозможно в силу сложности решаемой задачи (требуется сразу оттестировать большую и сложную структуру — всю программу или инструкцию).

Еще одно преимущество состоит в получении самодокументированных текстов программ. Самодокументированные программы получаются путем применения особого стандартизированного способа оформления текстов программ с использования комментариев и стандартных типовых структур кодирования.

Использование стандартных типовых структур предполагает особую декомпозицию алгоритма программы или эвроритма инструкции по принципу "от общего к частному", что требует от разработчика владения дедуктивным мышлением.

С появлением ЭВМ актуальным стал поиск способов описания вычислительных алгоритмов. В 60-х годах уже применялись два способа описания алгоритмов: словесный пошаговый и графический в виде схем алгоритмов программ (жаргонно: блок-схем алгоритмов).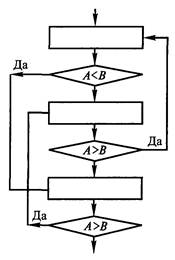

Рис. 5.1. Изображение алгоритма в форме графической схемы алгоритма

При словесно-пошаговом способе алгоритмы описывались по изложенному ниже принципу.

Шаг 1. Выполняется такое-то действие для того-то. Если получается, что А < В, то переходим к шагу 4.

Шаг 2. Выполняется такое-то действие для того-то.

Шаг 3. Если А > В, то переходим к выполнению шага 1.

Шаг 4. Выполняется такое-то действие для того-то.

Шаг 5. Если А > В, то переходим к выполнению шага 2.

Изображение того же алгоритма в форме схемы алгоритма приведено на рис. 5.1.

Недостатки каждого из способов приведены в табл. 5.1, из которой видно, что графический способ в виде схем алгоритмов программ облегчил лишь отслеживание передач управления и одновременно затруднил описание сути процессов (их комментирование).

Таблица 5.1

Недостатки словесно-пошагового и графического способов в виде схем описания алгоритмов программ

До конца 70-х годов проектная процедура получения алгоритмов базировалась на операционном (маршрутном) мышлении, которое закладывается еще в школе математическими и физическими учебными дисциплинами. Операционный подход не требует свободного владения дедуктивным мышлением и основан на более простом и уже освоенном индуктивном мышлении "от частного к общему". При операционном мышлении сначала записываются последовательные действия по главному основному маршруту. Затем эти действия дополняются операциями ветвления (if), операциями безусловного перехода (go to) и дополнительными действиями других маршрутов.

В результате использования операционного подхода получались программы (подпрограммы) со структурными элементами в виде операторов языка программирования и единственной сверхсложной структурой "вся программа" типа "спагетти" — множеством неупорядоченных передач управлений вперед и назад (см. рис. 5.1). Все это можно отнести и к большинству текстовых инструкций.

Программы, алгоритмы которых получаются операционным подходом, являлись практически несопровождаемыми. Даже при использовании графических схем алгоритмов их необходимо было дополнять достаточно длинными текстовыми описаниями. Эти текстовые описания должны были содержать огромное количество отдельных тестовых данных для отслеживания всех маршрутов вычислений с целью понимания алгоритма каждого отдельного маршрута. Сложность таких описаний приводила к несоответствию комментариев вычислительным процессам, а также к неоправданно длительному анализу алгоритма с просчетом трассы счета по всем маршрутам в процессе отладки. При использовании схем алгоритмов программ вне документации остается ход мыслей проектировщика по получению алгоритмов. Само вычерчивание схем алгоритмов программ занимает достаточно большое время. Огромное, поистине астрономическое число вычислительных маршрутов требовало подготовки астрономического количества тестов. Программы были ненадежными по сравнению с нынешними программами. Отладка программы в виде одной неразделимой структуры "спагетти" и длиной всего в 600 строк занимала время до полугода. Написание и отладка такой программы при современных технологиях производится программистом за два-три рабочих дня.

Согласно современным технологиям программирования, описания алгоритмов в словесно-пошаговой и графической формах в виде схем алгоритмов программ практически не используются. Их заменили самодокументированные тексты, состоящие из стандартных структур кодирования.

Составлению описания проектной процедуры предшествовали труды Дейкстры (с концепцией программирования без go to), одна из первых работ по структурному кодированию программ [9] и длительный опыт программирования и преподавания авторов.

Принципы описания последовательности действий для алгоритмов и эвроритмов практически не отличаются. В описаниях алгоритмов обычно присутствует лишь большая формализация. При написании программ программист обычно использует компьютер. Как правило, алгоритмы большинства процедур программ являются простейшими. Обычно код таких процедур опытные программисты пишут сразу сидя за монитором. Кодирование даже алгоритмически сложных процедур можно осуществлять с использованием компьютера, ведь современный компьютер отлично заменяет бумагу и карандаш! Просто надо параллельно в двух окнах монитора разрабатывать документальное описание процедуры и кодировать текст кода самой процедуры. Даже если код программы самодокументированный, отдельный документ будет содержать детальное описание структуры данных всей программы, а также наглядные тесты, детально характеризующие весь алгоритм. Наличие такой документации значительно упростит сопровождение программы.

Выполнение проектной процедуры начинается с первого шага, заключающегося в полном уяснении задачи на внешнем уровне. Этому помогают наборы тестовых примеров и модель "черного ящика". Наборы тестовых примеров способствуют учету всех возможных случаев работы алгоритма или эвроритма. Модель "черного ящика" способствует выявлению целевого назначения алгоритма, эвроритма (инструкции) или иной разрабатываемой искусственной системы. Модель "черного ящика" также помогает выявлять входную и выходную информацию программ и инструкций или определить материальные, энергетические и информационные входы и выходы иных разрабатываемых искусственных систем. Существуют алгоритмы и эвроритмы, составление которых можно начинать либо с анализа "черного ящика", либо с подготовки первичных тестов. Также известны алгоритмы, при разработке которых до качественного завершения работ приходилось многократно переключаться как на работу с "черным ящиком", так и на составление первичных текстов.

При разработке алгоритмов программ входная, промежуточная и выходная информация характеризуется структурой данных, размещенных в оперативной и во внешней памяти, и информацией, отображаемой на экране монитора.

При разработке эвроритмов инструкций входная, промежуточная и выходная информация характеризуется набором предметов (физических и документов) и их состоянием, например: пустой чайник; чайник, заполненный наполовину объема холодной водой; включен выключатель "сеть" в правом верхнем углу панели; документ по форме № 5 с заполненной первой графой. Здесь уместно дополнять описания предметов их рисунками. Учитывайте, что предметы изменяются во времени и пространстве.

Первичные тестовые примеры должны включать как обычные, так и стрессовые наборы тестовых входных данных. Каждый стрессовый набор тестовых данных предназначен для выявления реакции в особых случаях, например неверных действий пользователя, деления на ноль, выхода значения за допустимые границы, несоответствия инструкции состоянию дел и т. д. Любой набор тестовых данных должен содержать описание результата.

Второй шаг составления эвроритма или алгоритма начинается с разработки обобщающих тестов или обобщающего теста, включающих как можно в меньший набор тестов все случаи из первичных тестов.

На основе обобщающих тестов, а также выявленных входов и выходов системы готовится наглядный обобщающий тест или несколько наглядных обобщающих тестов. Наглядный тест должен отражать цепочку преобразования информации от исходной информации через промежуточную информацию и до результирующей информации. Главнейшее требование к обобщающему тесту — его наглядность в представлении порядка изменения информации. Известно, что при изучении геометрии успех решения задачи определяется наглядностью рисунков. Наглядные геометрические рисунки обычно получаются многовариантным их построением, и требуется приобретение некоторых навыков для развития искусства их выполнения. Все это относится и к составлению наглядных обобщающих тестов. Наглядность обобщающих тестов достигается правильным выбором способа отображения информации, который обеспечивает восприятие порядка преобразования информации.

Наглядные представления обычно основываются на модели типа абстракции данных, изложенной в гл. 1. Одной из ее форм может быть функциональная модель в виде набора диаграмм потоков данных (ДПД). Другая форма может соответствовать рисунку с рациональным способом размещения по его площади массивов с их именами, значениями элементов, значениями индексов элементов, значениями и именами простых переменных, соединенными стрелками по направлению передачи информации. Еще одной формой является форма, близкая к трассе счета, показывающая изменения значений переменных на шагах процесса. Возможны и иные формы, например таблицы правил.

Подчеркнем важность работы с данными. Данные во многом определяют алгоритмы. При решении одной и той же задачи, выбор разных структур данных приводит к совершенно различающимся алгоритмам или эвроритмам.

Дальнейшее выполнение проектной процедуры заключается в получении на основании модели абстракции данных модели процедурной абстракции, также изложенной в гл. 1.

Любые алгоритмы или эвроритмы должны состоять только из стандартных структур, каждая из которых строго имеет один информационный вход и один информационный выход. Использование иных (нестандартных) структур приводит либо к удлинению описания, либо к невозможности тестирования (из-за нереально огромного объема необходимых тестов), либо к потере понятности.

Потеря понятности происходит из-за того, что в неструктурированном алгоритме или эвроритме одни и те же части алгоритма или эвроритма при одних данных выполняют одно, а при других — другое. Поэтому части неструктурированных алгоритмов или эвроритмов невозможно однозначно характеризовать средствами естественного языка.

Структуре СЛЕДОВАНИЕ в инструкциях и программах соответствует строго одно действие.

Далее проектная процедура выполняется итеративными шагами: до достижения элементарных действий (элементарных операторов языка программирования или элементарных операций) отдельные структуры СЛЕДОВАНИЕ, из которых состоит описание любого алгоритма или эвроритма, декомпозируются с соблюдением принципа от общего к частному одной из трех стандартных структур (рис. 5.2): ЦЕПОЧКА СЛЕДОВАНИЙ; ЦЕПОЧКА АЛЬТЕРНАТИВ; ПОВТОРЕНИЕ.

В случае длинного алгоритма по исчерпанию информации обобщающего теста готовятся новые обобщающие тесты под все новые задачи структуры.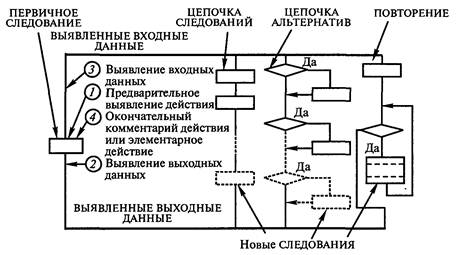

Рис. 5.2. Выявление вида очередной структуры при выполнении проектной процедуры разработки функциональных описаний

Из трех выявленных структур любая структура содержит в себе одну или несколько новых структур вида СЛЕДОВАНИЕ с более частными действиями. Эти новые СЛЕДОВАНИЯ могут подвергаться декомпозиции на следующей итерации выполнения проектной процедуры.

Итак, описания последовательности действий для алгоритмов и эвроритмов практически не различаются, поэтому их разработку рассмотрим совместно. Процесс кодирования программ, совмещенный с документированием, предполагает более разнообразные работы и требует особых знаний, поэтому кодирование программ рассмотрим отдельно. Отметим, что алгоритм ряда программ (например, математически не сложных) и код программ рождаются одновременно, причем рождаются на основе мыслей программиста. Отсюда следует, что признаки алгоритмических типовых структур и порядок их детализации, описанные в данном подразделе, являются одними и теми же для составления алгоритмов, эвроритмов и программ.

На каждой итерации проектной процедуры приходится решать задачу: "А какая именно из трех структур будет выявлена?" При решении данной задачи необходимую информацию можно получить лишь из анализа обобщающих тестов. Анализ тестов на предмет поиска самой главной на данный момент структуры является для начинающих весьма непростым делом. "Раскрепостить мышление" помогает набор признаков структур, изложенный в табл. 5.2, а также набор эвристических приемов, изложенный далее.

Таблица 5.2.

Сводная таблица характеристик структур и признаков структур

Набор эвристических приемов:

1. "Хорошие наглядные иллюстрации — залог успеха!".

2. "Думай от общего к частному!".

3. "Общий процесс определяет работу частных!".

4. "Это не главный процесс, вы увязли в частностях!".

5. "Не забывай вводить новые термины (имена переменных)!".

6. "Выделив главное действие, вы уже решаете более простую задачу!".

7. "Если закончилась информация в обобщающих тестах, то готовьте новые обобщающие тесты для решения все новых частных задач!".

8. "Если в процессе декомпозиции потребуется описать процесс выхода из какой-то точки описания в какую-то иную, то это значит, что были неправильно выполнены предшествующие детализации из-за неправильного выявления наиболее общего действия и требуется корректно переделать предшествующую работу!".

9. "Иногда очередная детализация не получается из-за неосознанной потребности по вводу вспомогательной переменной (флага события), характеризующей, произошло ли ранее какое-то событие!".

Каждое СЛЕДОВАНИЕ соответствует строго одному действию. Главное в действиях — глагол. Основное, что необходимо выполнить при описании отдельной структуры СЛЕДОВАНИЕ: в описании должна содержаться лишь одна мысль. Любая структура вида СЛЕДОВАНИЕ может быть описана простым распространенным предложением естественного (русского) языка. Например, "Следующее действие заключается в погрузке мебели в автомобиль". Однако учитывая то, что в случае составления алгоритмов программ суть типовых структур поясняется самими операторами языка программирования, применяется более краткое описание в виде неполного предложения без сказуемого. В последнем случае подлежащее образуют от глаголов. Например, "Погрузка мебели", "Решение квадратного уравнения", "Ввод данных".

Порядок детализации одиночного СЛЕДОВАНИЯ с использованием модели "черного ящика" показан на рис. 5.2; 5.3:

1) предварительное выявление сути действия;

2) выявление выходной информации, ибо выход определяет вход, а не наоборот;

3) выявление входной информации;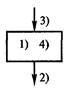

Рис. 5.3. Модель "черного ящика"

4) запись уточненного комментария сути действия или одного заключительного элементарного оператора.

При описании физических и технических систем необходимо использовать более полную модель "черного ящика" (см. рис. 2.2).

ЦЕПОЧКА СЛЕДОВАНИЙ соответствует однозначному описанию последовательности действий.

Признаком ЦЕПОЧКИ СЛЕДОВАНИЙ является никогда не нарушаемая последовательность действий (последовательность СЛЕДОВАНИЙ). ЦЕПОЧКЕ СЛЕДОВАНИЙ соответствует последовательность простых предложений и сложносочиненные предложения, которые лучше преобразовать в простые предложения.

Порядок детализации ЦЕПОЧКИ СЛЕДОВАНИЙ показан на рис. 5.4:

1) предварительное выявление сути действий каждого из СЛЕДОВАНИЙ, определение количества СЛЕДОВАНИЙ;

2) детализация каждого из СЛЕДОВАНИЙ как одиночного СЛЕДОВАНИЯ;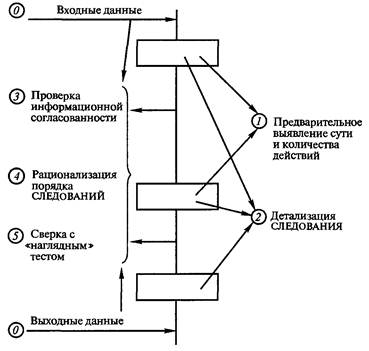

Рис. 5.4. Порядок действий при детализации структуры ЦЕПОЧКА СЛЕДОВАНИЙ

3) проверка информационной согласованности всех СЛЕДОВАНИЙ, а также входной и выходной информации всей ЦЕПОЧКИ СЛЕДОВАНИЙ;

4) рационализация порядка СЛЕДОВАНИЙ (сосредоточение СЛЕДОВАНИЙ, сотрудничающих в информационном обмене);

5) сверка с обобщающими тестами.

Отдельные СЛЕДОВАНИЯ структуры ЦЕПОЧКА СЛЕДОВАНИЙ в дальнейшем могут быть декомпозированы ЦЕПОЧКОЙ СЛЕДОВАНИЙ (более частных). Однако встречаются отдельные структуры СЛЕДОВАНИЯ, которые не могут быть декомпозированы ЦЕПОЧКОЙ СЛЕДОВАНИЙ. Такие СЛЕДОВАНИЯ могут быть описаны или структурой вида ЦЕПОЧКА АЛЬТЕРНАТИВ (ВЕТВЛЕНИЕ), или структурой вида ПОВТОРЕНИЕ (ЦИКЛ).

Признаком ЦЕПОЧКИ АЛЬТЕРНАТИВ или ВЫБОРА является одно или несколько действий, каждое из которых выполняется при определенном условии или не выполняется вообще (обязательно конечное число разных действий при разных условиях).

ЦЕПОЧКА АЛЬТЕРНАТИВ, в частном случае, может состоять из одной или нескольких простейших альтернатив с одним действием. Предложение простейшая АЛЬТЕРНАТИВА с одним действием имеет следующую конструкцию: "Если выполняется какое-то условие, то выполняется такой-то процесс (СЛЕДОВАНИЕ)". (В противном случае СЛЕДОВАНИЕ пропускается.) Предложение АЛЬТЕРНАТИВА из двух действий имеет следующую конструкцию: "Если выполняется какое-то условие, то выполняется СЛЕДОВАНИЕ 1, в противном случае выполняется СЛЕДОВАНИЕ 2". В принципе структура АЛЬТЕРНАТИВА из двух действий эквивалентна цепочке из двух простейших альтернатив с одним действием. При детализации процессов, включающих более двух альтернатив, может быть получена единая структура— ВЫБОР в виде цепочки последовательно записанных структур АЛЬТЕРНАТИВА с одним действием. Здесь следует отметить, что от внешне похожей ЦЕПОЧКИ СЛЕДОВАНИЙ, каждое СЛЕДОВАНИЕ которой является простейшей АЛЬТЕРНАТИВОЙ с одним действием, структура ВЫБОР отличается таким свойством, что при выполнении всей ЦЕПОЧКИ АЛЬТЕРНАТИВ может выполняться лишь одно из альтернативных СЛЕДОВАНИЙ или ни одного из альтернативных СЛЕДОВАНИЙ.

Пример условий альтернатив в случае структуры ВЫБОР:

Если А < В, то выполнить СЛЕДОВАНИЕ1;

Если А = В, то выполнить СЛЕДОВАНИЕ2;

Если А > В, то выполнить СЛЕДОВАНИЕЗ.

АЛЬТЕРНАТИВОЙ с одним действием можно осуществить досрочное прекращение процесса выполнения алгоритма в том случае, который соответствует обнаружению условий невозможности правильного дальнейшего выполнения алгоритма или эвроритма.

Детализациям всех последующих структур предшествует нулевое действие — запись в начале и в конце входных и выходных данных, выявленных в процессе детализации предшествующих им СЛЕДОВАНИЙ.

Порядок детализации ЦЕПОЧКИ АЛЬТЕРНАТИВ показан на рис. 5.5:

1) предварительное выявление сути действия каждого из СЛЕДОВАНИЙ альтернативных действий, определение количества таких СЛЕДОВАНИЙ;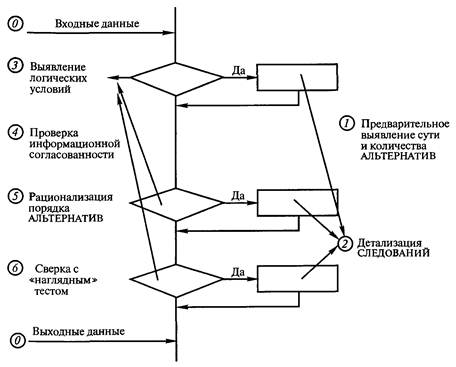

Рис. 5.5. Порядок действий при детализации цепочки АЛЬТЕРНАТИВ, согласно проектной процедуре разработки функциональных описаний

2) детализация каждого из СЛЕДОВАНИЙ как одиночного СЛЕДОВАНИЯ;

3) выявление и запись логического условия выполнения каждого из альтернативных СЛЕДОВАНИЙ;

4) проверка информационной согласованности всех СЛЕДОВАНИЙ и логических условий в цепочке, а также входной и выходной информации всей ЦЕПОЧКИ АЛЬТЕРНАТИВ;

5) рационализация порядка альтернатив;

6) проверка выполнения всех маршрутов на тестах, полученных из обобщающего теста.

Признаком ПОВТОРЕНИЯ является многократно выполняемое действие (но обязательно конечное число раз). ПОВТОРЕНИЯМ соответствуют мысли: "Это действие должно быть выполнено пять раз"; "Это действие выполняется многократно до наступления такого-то события". Признаки ПОВТОРЕНИЙ — переменное количество АЛЬТЕРНАТИВ, любая мысль о возврате "назад", чтобы повторить какие-то действия. Часто главный более общий процесс вида ПОВТОРЕНИЕ прячется в контексте "и т. д." или "и т. п.", "это совсем просто", или даже в многоточиях "…".

Предложение вида ПОВТОРЕНИЕ может быть записано или в форме ПОВТОРЕНИЕ "ДО" (ЦИКЛ "ДО"), или в форме ПОВТОРЕНИЕ "ПОКА" (ЦИКЛ "ПОКА").

Предложение ПОВТОРЕНИЕ "ДО" имеет следующую конструкцию: "До выполнения какого-то условия многократно выполнять СЛЕДОВАНИЕ".

Предложение ПОВТОРЕНИЕ "ПОКА" имеет следующую конструкцию: "Пока выполняется какое-то условие, многократно выполнять СЛЕДОВАНИЕ".

Разница между предложениями ПОВТОРЕНИЕ "ДО" и ПОВТОРЕНИЕ "ПОКА" заключается в том, что, согласно первому предложению, действие СЛЕДОВАНИЕ должно быть выполнено хотя бы один раз, а согласно второму, — СЛЕДОВАНИЕ может не выполняться ни разу.

Структура НЕУНИВЕРСАЛЬНОЕ ПОВТОРЕНИЕ или просто обеспечивает заданное количество повторений какого-либо процесса или выполнение какого-то процесса при значении переменной цикла, значение которой изменяется по правилам арифметической прогрессии.

Порядок детализации ПОВТОРЕНИЙ показан на рис. 5.6.

Детализация повторений ведется в вариантной постановке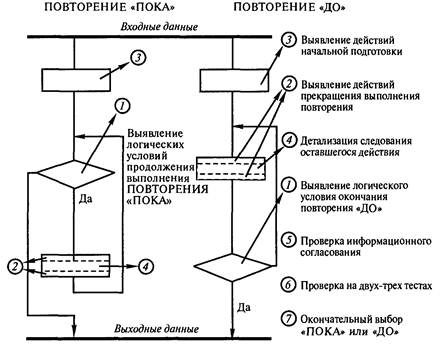

Рис. 5.6. Порядок действий при детализации ПОВТОРЕНИЙ

1) выявление и запись логического условия завершения ПОВТОРЕНИЯ "ДО" или условия продолжения выполнения ПОВТОРЕНИЯ "ПОКА";

2) выявление действий прекращения выполнения повторения;

3) выявление действий СЛЕДОВАНИЯ подготовки выполнения ПОВТОРЕНИЯ;

4) детализация СЛЕДОВАНИЯ оставшегося действия как одиночного СЛЕДОВАНИЯ;

5) проверка информационной согласованности всех СЛЕДОВАНИИ, логических условий, а также входной и выходной информации всего ПОВТОРЕНИЯ;

6) проверка на 2–3 тестах, полученных из обобщающего теста;

7) окончательный выбор варианта реализации ПОВТОРЕНИЯ в виде структуры ПОВТОРЕНИЕ "ПОКА" или в виде структуры ПОВТОРЕНИЕ "ДО".

Первые попытки работы с проектной процедурой требуют огромного количества листов бумаги, но это необходимо, так как позволяет внимательно рассмотреть отдельный лист и относительно безболезненно переделать неудачные детализации. По достижении некоторого опыта можно все большую часть работы делать без ее записи на отдельных листах. Однако первая работа выполняется строго на отдельных листах. Особенно это важно в случае наличия опытного специалиста, который по листам документа сможет выявить дефекты навыков у обучаемого, а также выдать обучаемому серию индивидуальных подсказок.

Выполнение проектной процедуры начинается с подготовки и рассмотрения тестовых примеров для детализации всего описываемого процесса в виде одного СЛЕДОВАНИЯ.

На отдельном листе составляется множество тестовых примеров, охватывающих все случаи вычислений или действий по инструкции.

Параллельно с подготовкой тестов осуществляем анализ модели "черного ящика". Берем еще один чистый лист бумаги, внизу листа записываем термины выходных объектов и их состояния. Применительно к алгоритмам определяем структуру данных: вводим обозначения переменных, последовательностей, векторов, матриц и определяем порядок размещения в них информации. Применительно к физическим системам определяем месторасположения и состояния объектов. Например, чайник без воды находится на полке. Результат действий — чайник, заполненный кипятком до половины объема, находится на плите. Выход определяет вход, а не наоборот! Поэтому сначала записываются результаты действий и лишь затем состояния объектов до действий.

Далее в верхней части листа записываются термины входных объектов и состояния входных объектов. В середине листа записывается одно простое распространенное предложение, характеризующее процесс преобразования входной информации в выходную информацию. Многократным анализом входа, выхода и сути предложения уточняется вся информация листа.

На основе совокупности тестов на отдельном листе составляем один или несколько обобщающих тестов. При этом нужно спроектировать рациональную форму иллюстрирования: например, рисунки промежуточных состояний данных процесса или таблицы состояний данных или физических объектов. Обобщающий тест необходим для понимания сути функционирования процесса. На обобщающем тесте приводятся обозначения всех входных, выходных и внутренних переменных или состояний физических объектов. Из теста должны быть видны все процессы преобразования входной информации в результат.

Обучаемым, которые находятся на начальной стадии изучения, рекомендуется предварительно описать протекание процесса по принципу: "Как можешь!" Качество описания должно соответствовать попытке объяснения процесса какому-то заурядному человеку или даже ребенку. Данный текст поможет (с использованием признаков) отличить общие действия от частных.

Наконец, приступаем к составлению семантического скелета структурированного описания функционирования.

При обучении детализации очередной структуры следует осуществлять на отдельном листе. При детализации ЦЕПОЧЕК СЛЕДОВАНИЙ рекомендуется ориентировать лист узкой стороной вверх, а при детализации ЦЕПОЧЕК АЛЬТЕРНАТИВ и ПОВТОРЕНИЙ лист лучше ориентировать широкой стороной вверх (это позволит размещать на листе трассы просчета тестов). Предварительно в верхней части листа записывается предложение, которое было получено ранее из детализации каждого из этих процессов в виде одного СЛЕДОВАНИЯ. Под ним записывается входная информация СЛЕДОВАНИЯ, а внизу листа — выходная информация. Далее осуществляется сама детализация, результаты которой после проверки на тестовых примерах и литературной обработки переносятся в чистовик описания алгоритма в целом.

При детализации ЦЕПОЧКИ СЛЕДОВАНИЙ равномерно по свободной части листа записываются предложения сути последовательно выполняемых действий (конкретный смысловой комментарий к процессу). Далее осуществляется работа над каждым из них как над отдельным СЛЕДОВАНИЕМ. Далее осуществляется проверка информационной согласованности следований и рационализируется их порядок, уточняется суть СЛЕДОВАНИЙ. При проверке необходимо убедиться, что для последующих СЛЕДОВАНИЙ данные уже были определены предшествующими СЛЕДОВАНИЯМИ.

При детализации ЦЕПОЧКИ АЛЬТЕРНАТИВ равномерно по свободной части листа записываются (в количестве альтернативных действий) конструкции в виде нужного количества следующих последовательных предложений: слово "Если", несколько чистых строк для поля условия, слова "то выполняется действие", далее оставляется несколько чистых строк для предложения СЛЕДОВАНИЕ (конкретный смысловой комментарий процесса).

После детализация всех записанных СЛЕДОВАНИЙ как одного СЛЕДОВАНИЯ осуществляется запись условий выполнения альтернативных процессов. Далее осуществляется проверка информационной согласованности входа и выхода каждого из СЛЕДОВАНИЙ, их условий выполнения, а также входной и выходной информации всей ЦЕПОЧКИ АЛЬТЕРНАТИВ. Цепочка только из двух альтернатив может быть описана предложением вида: "Если выполняется условие (конкретное условие выполнения действия по ТО), то выполняется процесс (конкретный смысловой комментарий процесса), в противном случае выполняется иной процесс (конкретный смысловой комментарий процесса).

При детализации ПОВТОРЕНИЙ на свободной части листа записываются слова обоих заготовок для ПОВТОРЕНИЯ "ДО" и ПОВТОРЕНИЯ "ПОКА". Каждая заготовка начинается с чистых строк для будущего СЛЕДОВАНИЯ определения подготовки повторяющихся действий. Далее для ПОВТОРЕНИЯ "ДО": записывается строка "До выполнения условия окончания повторяющегося процесса"; оставляется несколько чистых строк для записи условия окончания повторяющегося действия; записывается строка "многократно выполняется следующее действие:…". Для ПОВТОРЕНИЯ "ПОКА" записывается строка "Пока выполняется условие"; оставляется несколько чистых строк для записи условия продолжения выполнения повторяющегося действия; записывается строка "многократно выполняется следующее действие:…". Под этими строками на обеих заготовках оставляются чистые строки для СЛЕДОВАНИЯ, определяющего окончание повторения процесса и СЛЕДОВАНИЯ многократно выполняемого действия. Заполнение заготовок осуществляется в следующем порядке: сначала условие окончания (продолжения для ПОВТОРЕНИЯ "ПОКА") выполнения повторяющегося действия; затем записывается СЛЕДОВАНИЕ, определяющее окончание повторения процесса; потом — СЛЕДОВАНИЕ определения подготовки повторяющихся действий и в последнюю очередь — СЛЕДОВАНИЕ многократно выполняемого действия. Далее осуществляется проверка информационной согласованности входа и выхода каждого из СЛЕДОВАНИЙ, условия выполнения действия, а также входной и выходной информации всей структуры. Если до начала детализации не было ясно, какой из вариантов повторений рациональнее детализировать в первую очередь, то последовательно детализируются обе заготовки. Окончательный вариант отбирается путем их сравнения по критериям краткости и понятности.

По окончании детализации структурных отдельных частей документа необходимо произвести его сборку. При сборке обычно требуется литературное редактирование документа как единого целого. После смысловой и литературной обработки результат исследований процесса переносится в чистовик. Главный принцип — передай другим ход своих мыслей так, чтобы они смогли понять, но при этом не следует переусердствовать в деталях. Излишние комментарии могут вызвать раздражение читателя и усилить непонимание.

Ниже показано пошаговое выполнение проектной процедуры на примере разработки описания процесса "Кипячение воды в чайнике". Дополните данное описание наглядными рисунками на листе 1 самостоятельно.

Лист 2. Анализ процесса как одного СЛЕДОВАНИЯ.

Первичное описание сути действия: "Кипячение воды в чайнике".

Выход: Чайник, заполненный кипятком до половины объема, находится на газовой плите. Конфорка выключена.

Вход: Чайник без воды находится на полке. Конфорка выключена. Требуемый объем кипятка — половина чайника.

Окончательное описание сути действия: "Получение чайника, заполненного кипятком до заданного объема".

Работаем с тестами. Из тестов выясняем, что получить кипяток невозможно без воды, спичек и газа. Спички могут закончиться в процессе зажигания газа. Может закончиться вода в процессе заполнения чайника. Также может закончиться газ в магистрали. Принимаем, что выявление данных фактов будет осуществлено в процессе выполнения инструкции, поэтому информацию о наличии спичек, воды и газа исключаем из состава входной информации.

Нами получено СЛЕДОВАНИЕ (рис. 5.7).

Лист 3 — содержит изображение процессов инструкции в наглядной форме. Разработайте его самостоятельно.

Лист 4 — может содержать описание процесса "Получение чайника, заполненного кипятком до заданного объема", выполненное любым доступным способом.

Рис. 5.7. Детализация с применением графического изображения "черного ящика"

Лист 5. Декомпозиция процесса "Получение чайника, заполненного кипятком до заданного объема".

Первоначально на лист переносим информацию предшествующей структуры СЛЕДОВАНИЕ, получаем макет листа, представленный на рис. 5.8.

Далее, исходя из соображений, что для этого процесса необходимо выполнить ряд последовательных действий, получаем макет листа с ЦЕПОЧКОЙ СЛЕДОВАНИЙ, представленный на рис. 5.9.

После детализации каждого из следований, проверки информационной согласованности и уточнения сути следований в цепочке получаем макет листа, изображенный на рис. 5.10.

Проверка информационного согласования выявила, что действие 2 не может быть ранее действия 1 из соображений экономии газа. Чайник нельзя ставить на конфорку до зажигания газа из-за опасности закопчения донышка копотью спички. Аналогично проверялась последовательность остальных действий.

Действие 1 может быть декомпозировано еще одной ЦЕПОЧКОЙ СЛЕДОВАНИЙ, изображенной на рис. 5.11.

Рис. 5.8. Первоначальный вид листа 5

Рис. 5.9. Вид листа 5 после предварительного выявления сути действий

Действие 1 "Заполнение чайника водой" может быть декомпозировано еще одной ЦЕПОЧКОЙ СЛЕДОВАНИЙ, изображенной на рис. 5.11.

Действие 4 "Наполнение чайника водой", показанное на рис. 5.11, декомпозируется ПОВТОРЕНИЕМ, представленным на рис. 5.12.

Рис. 5.10. Окончательный вид листа

Декомпозиция цепочкой СЛЕДОВАНИЙ действия "Анализ процесса заполнения чайника на форс-мажорные обстоятельства" представлена на рис. 5.13.

Рис. 5.11. Детализация СЛЕДОВАНИЯ "Заполнение чайника водой", выявленного на рис. 5.10

Действие "Форс-мажорное завершение инструкции" представляет цепочку СЛЕДОВАНИЙ, показанной на рис. 5.14. Обратим внимание на то, что выходная информация аварийного завершения инструкции определяется входной информацией всей инструкции (см. рис. 5.7).

Рис. 5.12. Декомпозия ПОВТОРЕНИЕМ действия 4 "Наполнение чайника водой" (см. рис. 5.11)

Рис. 5.13. Декомпозиция ЦЕПОЧКОЙ СЛЕДОВАНИЙ действия "Анализа процесса заполнения чайника на форс-мажорные обстоятельства" (см. рис. 5.12)

Рис. 5.14. Декомпозиция действия "Форс-мажорное завершение инструкции" представляет цепочку СЛЕДОВАНИЙ

Действие 2 (см. рис. 5.10) "зажигание газовой горелки" декомпозируется циклом: пока не зажглась конфорка или не выявлены форс-мажорные обстоятельства, многократно выполнять действие "Зажигание конфорки". Дальнейшее развитие алгоритма позволило выявить структуры, изложенные далее.

Действие (СЛЕДОВАНИЕ) "Зажигание конфорки" представляет собой ЦЕПОЧКУ СЛЕДОВАНИЙ: "Зажигание спички", "Включение газа", "Поджигание газа", "Отключение газа при неудаче", "тушение спички", "выбрасывание спички". Форс-мажорными обстоятельствами является отсутствие газа или окончание спичек. Им соответствует логическая переменная.

Действие (СЛЕДОВАНИЕ) "Отключение газа при неудаче" представляет собой альтернативу: если газ не зажегся, а спичка прогорела, то необходимо закрыть газ.

Здесь выявлена предшествующая недоработка с выходными данными действия 2. Ведь по окончании действия 2 конфорка может быть как включена, так и не включена. Исправить ситуацию можно двумя способами. По первому способу за действием 2 можно вставить простейшую альтернативу с одним действием: если выявлены форс-мажорные обстоятельства, то аварийно завершить инструкцию. Согласно второму способу, действия 3, 4, 5 могут быть представлены одним СЛЕДОВАНИЕМ, внутри которого должна находиться ЦЕПОЧКА АЛЬТЕРНАТИВ последовательного выполнения каждого из прежних действий 3, 4, 5 при условии отсутствия выявления форс-мажорных обстоятельств.

Ниже приведен пример описания программы "Редактор текстов", составленный одним из обучаемых. В примере приводится сначала внешняя функциональная спецификация, а затем внутренняя спецификация.

Программа "Редактор текстов" предназначена для создания новых и корректировки существующих текстовых файлов MS DOS в диалоговом (пользователь-ЭВМ) режиме работы. ЭВМ формирует экран с окном, в котором отображен участок текста из текстового файла (макет экрана соответствует внутреннему редактору программы Norton Commander). Пользователю обеспечивается возможность вставки в текст в окне экрана любого символа клавиатуры за символом, отмеченным на экране курсором. Исключение составляет ряд символов, которые являются признаками команд управления или незадействованными символами (приводится список символов). После подачи пользователем команды записи все изменения текста, осуществленные пользователем, записываются в файл.

Основной принцип работы редактора текстов состоит в переносе строк текста из необходимых участков файла сначала в буферный массив памяти длиной в 65535 байт (символов) с дальнейшим копированием необходимых строк из буферного массива в окно экрана.

Запуск программы осуществляется командой с указанием имени редактируемого файла. Далее, пока не будет указано корректное имя файла, может начать многократно выполняться алгоритм "Запрос пользователя на ввод или корректировку имени файла".

Затем задаются начальные значения структурированной переменной "Система координат", в которой имеются поля: "Положение курсора относительно файла"; "Положение курсора относительно буферного окна редактора"; "Положение буферного окна редактора относительно файла".

После осуществляется очистка буферного массива редактора строковых переменных из 5 * 23 = 115 строк длиной по 225 символов.

Далее при параметре "Первая строка файла" выполняется алгоритм "Загрузка строк файла, начиная с указанной строки в буферный массив редактора". Потом до подачи пользователем одной из команд завершения редактирования с сохранением информации (или без сохранения) выполняется главный цикл программы. Наконец, если была дана команда завершения с сохранением информации, то информация из буферного массива переписывается в файл. Выполнение программы завершается очисткой экрана.

Контроль имени редактируемого файла состоит в следующем. Если файл с указанным именем отсутствует на диске, то выводится предупреждающее сообщение о создании нового "пустого" файла. Если пользователь не указал имя редактируемого файла или отказался работать с созданным "пустым" файлом, то происходит аварийное завершение программы с пояснением причины завершения.

Внутри главного цикла программы выполняется ряд из трех последовательных действий. "Алгоритм отображение" отображает на экране 23 строки текста из буферного массива, начиная с заданной строки. Далее устанавливается курсор дисплея на заданную позицию экрана. Осуществляется ввод кода нажатой клавиши. Если код нажатой клавиши соответствует управляющей клавише, то выполняется одно из альтернативных действий по выполнению команды, которая соответствует данной клавише. В противном случае осуществляется вставка символа в текст.

Алгоритм Нелдера — Мида является широко известным и применяется в качестве алгоритма прямого поиска локального экстремума вещественных функций от 2 до 6 вещественных переменных.

Следующий абзац содержит фрагмент текста из книги Д. Химмельблау [26], в котором содержится часть описания алгоритма Нелдера — Мида (метода деформируемого многогранника).

В методе Нелдера и Мида минимизируется функция n независимых переменных с использованием n + 1 вершин деформируемого многогранника в Eⁿ. Каждая вершина может быть идентифицирована вектором x. Вершина (точка) в Eⁿ, в которой значение f(x) максимально, проектируется через центр тяжести (центроид) оставшихся вершин. Улучшенные (более низкие) значения целевой функции находятся последовательной заменой точки с максимальным значением f(x) на более "хорошие" точки, пока не будет найден минимум f(x).

Начальный многогранник обычно выбирается в виде регулярного симплекса (но это не обязательно) с точкой в начале координат. Процедура отыскания вершины в Eⁿ, в которой f(x) имеет лучшее значение, состоит из следующих операций:

Отражение — проектирование x^(k)_h через центр тяжести в соответствии с соотношением x^(k)_n+3 = x^(k)_n+2 + α(x^(k)_n+2 — x^(k)_h), где α > 0 является коэффициентом отражения; x^(k)_n+2 — центр тяжести, x^(k)_h — вершина, в которой функция f(x) принимает наибольшее из n + 1 ее значений на k-м этапе.

Растяжение выполняется, если f(x^(k)_n+3) ≤ f(x^(k)_i), то вектор (x^(k)_n+3 — x^(k)_n+2) растягивается в соответствии с соотношением x^(k)_n+4 = x^(k)_n+2 + γ(x^(k)_n+3 — x^(k)_n+2), где γ — коэффициент растяжения. Если f(x^(k)_n+4) < f(x^(k)_i), то x^(k)_h заменяется на x^(k)_n+4 и процедура продолжается с шага 1 (k = k + 1), иначе x^(k)_n заменяется на x^(k)_n+3, процедура продолжается с шага 1 (k = k + 1).

Сжатие — если f(x^(k)_n+3) > f(x^(k)_i) для всех i ≠ h, то вектор (x^(k)_h — x^(k)_n+2) сжимается в соответствии с формулой x^(k)_n+5 = x^(k)_n+2 + β(x^(k)_h — x^(k)_n+2), где 0 < β < 1 представляет собой коэффициент сжатия. Затем x^(k)_h заменяется на x^(k)_n+5 и переходит на шаг 1 (k = k + 1).

Редукция — если f(x^(k)_n+3) > f(x^(k)_h), все векторы (x^(k)_i — x^(k)₁), i = 1…n + 1 уменьшаются в 2 раза с отсчетом от x^(k)₁ в соответствии с формулой x^(k)_i = x^(k)_i + 0,5(x^(k)_i — x^(k)₁), i = 1…n + 1. Затем возвращаемся к шагу 1 для продолжения поиска на k + 1 шаге.

Критерий окончания поиска, использованный Нелдером и Мидом, состоял в проверке условия среднего квадратичного отклонения функций f(x^(k)_i) от произвольного малого числа ε.

Химмельблау воспользовался традиционным математическим стилем для изложения описания алгоритма. Алгоритм имеет структуру вида "спагетти", что видно из схемы алгоритма, разработанной автором (рис. 5.15). Схема в виде "спагетти" — это скрытые go to, которые мы обнаруживаем в тексте программы, разработанной автором. Он же приводит графические рисунки принципа расчета точек и графический рисунок последовательности продвижения лучших точек симплекса по шагам метода при решении тестовой задачи. Затратив 11 страниц текста, приведя текст неструктурированной программы на 12 страницах, автор книги [26] так и не сумел понятно описать свой алгоритм.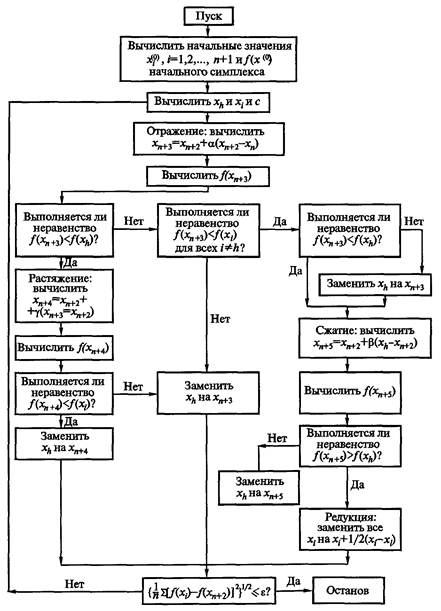

Рис. 5.15. Схема алгоритма, разработанная Д. Химмельблау

Сравните способ подачи описания алгоритма, составленный автором [22], и функциональное описание алгоритма после рефакторинга. Функциональное описание алгоритма приведено ниже.

Особенностью алгоритма является продвижение к экстремуму целым облаком пробных точек, который условно назван симплексом (деформируемым многогранником). Общее число точек в симплексе равно увеличенному на единицу числу переменных поиска. Продвижение к экстремуму не по линии от одной точки к другой, а внутри какого-то множества пробных точек обеспечило нереагирование на мелкие дефекты целевой функции и прохождение относительно "широких" оврагов.

Вводимая информация:

n — число переменных минимизируемой функции;

X⁰ = (x⁰₁, x⁰₂…, x⁰_n) — точка первого начального приближения;

h — шаг регуляризации симплекса;

ε_x — погрешность нахождения экстремума по параметрам.

Работа алгоритма начинается с начальной подготовки симплекса точек. После выполнения процедур регуляризация симплекса и расчета значений целевой функции во всех точках симплекса имеет вид

Процедура регуляризации симплекса состоит в копировании во все поля значений аргументов симплекса значения вектора X⁰, и далее производятся изменения значений диагональных компонент векторов с номерами от 2 до n + 1 путем их увеличения на шаг регуляризации симплекса h.

В симплексе Q₁, Q₂, Q₃…, Q_n+1 — это рассчитанные значения минимизируемой функции при соответствующих по строке значениях аргументов минимизируемой функции.

Далее до выполнения условия окончания поиска осуществляются итерации (шаги) поиска. Условием окончания поиска этого метода является неудаленность от лучшей точки симплекса остальных точек симплекса более чем на e²_x.

Каждая итерация начинается с нахождения номеров l и k, соответственно лучшей и худшей по значению функции точек симплекса. Далее осуществляется расчет точки X_ц — положения центра масс всех точек симплекса за исключением наихудшей точки 1. Это позднее улучшение алгоритма. Д. Химмельблау не исключал наихудшей точки.

где n — количество точек в симплексе; i — номер компоненты вектора X(i = 1, 2…, n); j — номер точки в симплексе.

Считаются нулевыми значения x_kj слагаемых сумм, где k — номер наихудшей точки.

При работе метода на каждой из итерации может вычисляться одна из особых пробных точек: а — точка отражения, р — точка растяжения, у — точка сжатия. Точки вычисляются по формулам:

X_α = X_ц + α(X_ц — X_k), X_β = X_ц + β(X_ц — X_k), X_γ = X_ц + γ(X_ц — X_k).

Целесообразно эти похожие формулы реализовать одной функцией.

Значения коэффициентов α = 1, β = 0,5 и γ = 2 подобраны экспериментальным путем (в оригинале описания алгоритма эти значения можно выявить лишь из текста программ). Расчет точек α, β, γ целесообразно осуществлять одной процедурой с параметром в виде значений коэффициентов α, β, γ.

После расчета точки X_ц вычисляется пробная точка α. Далее выполняется одно из альтернативных действий.

Если Q_α ≤ Q₁, то выполняются действия достижения сильного успеха. Если Q₁ ≤ Q_α < Q_k, то имеется слабый успех, а точка α записывается на место k-точки. Если Q_α ≥ Q_k, то выполняются действия отсутствия успеха. Рассчитывается X_β и Q_β. Далее, если Q_β ≤ Q_k, то точка β записывается на место k-точки, иначе, если точка β хуже точки k, выполняется процедура редукции симплекса и процедура расчета значения функции в точках симплекса.

Действия достижения сильного успеха. Рассчитывается X_γ и Q_γ. Наилучшая из точек α или β записывается на место наихудшей k-точки симплекса.

Действия отсутствия успеха. Рассчитывается X_β и Q_β. Далее выполняется действие по изменению симплекса при отсутствии успеха.

Действие по изменению симплекса при отсутствии успеха представляет собой альтернативу: если Q_β ≤ Q_k, то точка β записывается на место k-точки, иначе, если точка β хуже точки k, выполняется процедура редукции симплекса.

При выполнении процедуры редукции симплекса все точки симплекса стягиваются к лучшей точке симплекса на половину своего прежнего удаления и далее выполняется процедура расчета значений целевой функции во всех точках симплекса.

Обычно разработку алгоритмов программ совмещают с кодированием текста программы. Отдельное от программирования написание алгоритмов практически ничем не отличается от написания инструкций.

Кодирование программы должно осуществляться только с использованием стандартных структур! Запрещено использование меток, операторов безусловного перехода на метку (go to), операторов досрочного выхода из структуры break!

При кодировании на языке С оператор break может использоваться только при кодировании структуры switch.

При использовании другого процедурно-ориентированного языка программирования (не Pascal) необходимо предварительно закодировать на используемом языке программирования все описанные в этом подразделе стандартные структуры без изменения их логики!

Так, при программировании на языке С структура УНИВЕРСАЛЬНЫЙ ЦИКЛ — "ДО" будет включать операцию "!" (НЕ):

/* подготовка цикла */

do

{

/* Тело цикла */

…

}

while (! (L));

В приведенной выше структуре ненулевое значение переменной L соответствует окончанию выполнения цикла, а не его продолжению выполнения, как в операторе языка программирования! Использование "линией" операции (!) НЕ никак не удлинит программу. Современные компиляторы автоматически инвертируют логическое условие завершения цикла.

Структуре СЛЕДОВАНИЕ в программах могут соответствовать: выполнение всей программы; вызов процедуры.

Согласно стандарту проекта, АЛЬТЕРНАТИВА имеет четыре конструкции. Рассмотрим их запись на языке программирования Pascal.

Конструкция для одной альтернативы:

if L then begin

{Действие при L=True}

…

end;

Конструкция для двух альтернатив:

if L then begin

{Действие при L=True}

…

end

else

begin

{Действие при L=False}

…

End;

Первый вариант конструкции для нескольких альтернатив (ВЫБОРА):

if L1 then Begin

{Действие при L1=True}

end;

…

if L2 then

begin

{Действие при L2=True}

…

end;

if L3 then

begin

{Действие при L3=True}

…

end;

Второй вариант конструкции для нескольких альтернатив (ВЫБОРА):

Switch:= 0;

L1:=…;

L2:=…;

L3:=…;

…

if L1 then Switch:= 1;

if L2 then Switch:= 2;

if L3 then Switch:= 3;

…

case Switch of

1:begin

{Действие при L1=True}

…

end;

2:begin

{Действие при L2=True}

…

end;

3:begin

{Действие при L3=True}

…

end;

else

begin

{Вывод сообщения об ошибочном кодировании модуля}

…

end;

end; {End of Case}

Рассмотрим запись вариантов кодирования структуры АЛЬТЕРНАТИВА на языке программирования С.

Конструкция для одной альтернативы:

if (L)

{

/*Действие при L ≠ 0*/

…

}

Конструкция для двух альтернатив:

if (L)

{

/*Действие при L ≠ 0*/

…

}

else

{

/*Действие при L = 0*/

…

}

Первый вариант конструкции для нескольких альтернатив (ВЫБОРА)

if (L1)

{

/*Действие при L1 ≠ 0*/

…

}

else if (L2)

{

/*Действие при L2 ≠ 0*/

…

}

else if(L3)

{

/*Действие при L3 ≠ 0*/

…

}

…

}

Второй вариант конструкции для нескольких альтернатив (ВЫБОРА):

Selector = 0;

L1 =…;

L2 =…;

L3 =…;

…

if (L1) Selector = 1;

else if (L2) Selector = 2;

else if (L3) Selector = 3;

…

switch (Selector)

case 1:

/*Действие при L1 ≠ 0*/

…

break;

case 2:

/*Действие при L2 ≠ 0*/

…

break;

case 3:

/*Действие при L3 ≠ 0*/

…

break;

default:

/*Вывод сообщения об ошибочном кодировании модуля*/

exit (-1);

} /*Конец switch*/

Правая конструкция соответствует очень сложной логике условий. В простейших случаях допускается упрощенная кодировка (первый пример на Pascal, второй на Q:

if a > b then x:=y+3 else x:=у+6; {Язык Pascal}

if (a > b) x=y+3; else x=у+6; /*Язык С*/

ВЫБОР из двух и более АЛЬТЕРНАТИВ нельзя кодировать при помощи вложения других структур простейших АЛЬТЕРНАТИВ из-за большой вероятности ошибок.

Порядок детализации структур АЛЬТЕРНАТИВА:

1) в зависимости от количества альтернативных действий записываются все операторы структуры;

2) определяются сами альтернативные действия как СЛЕДОВАНИЯ;

3) записываются логические условия альтернативных действий;

4) проверяется информационная согласованность логических условий и действий;

5) на нескольких текстовых примерах осуществляется проверка. ПОВТОРЕНИЯ в программировании называются циклами.

Обычно стандартом проекта предусмотрен ряд конструкций циклов. Неуниверсальный ЦИКЛ-ДО имеет две конструкции и используется для задания заданного числа повторений. Рассмотрим их запись на языке программирования Pascal.

Конструкция по возрастанию:

for i:=3 to 5 do begin

{тело цикла i=3,4,5}

…

end;

Конструкция по убыванию:

for i:=5 downto 3 do begin

{тело цикла i=5,4,3}

…

end;

Рассмотрим запись вариантов кодирования структуры неуниверсальный ЦИКЛ-ДО на языке программирования С.

Конструкция по возрастанию:

for (i=3; i<=5; i++)

{

/*тело цикла i=3,4,5*/

…

}

Конструкция по убыванию:

for (i=5; i>=3; i-)

{

/*тело цикла i=5,4,3*/

…

}

Здесь i — переменная цикла. Обычно эти циклы не требуют после кодирования дополнительного тестирования.

Универсальные циклы имеют конструкции ЦИКЛ-ДО и ЦИКЛ-ПОКА. Их запись на языке Pascal приведена ниже:

Универсальный ЦИКЛ-ПОКА:

{Подготовка}

while L do

begin

{Тело цикла}

…

end;

Универсальный цикл ЦИКЛ-ДО:

{Подготовка}

repeat

{Тело цикла}

…

until L;

Ниже приведена запись тех же структур на языке С:

Универсальный ЦИКЛ-ПОКА:

/*Подготовка*/

while (L)

{

/*Тело цикла*/

…

}

Универсальный ЦИКЛ-ДО:

/*Подготовка*/

do

{

/* Тело цикла */

…

}

while (!(L))

Здесь L логическое выражение. Его значение True является условием продолжения выполнения ЦИКЛ-ПОКА или условием окончания выполнения ЦИКЛ-ДО. Подготовка и тело цикла являются СЛЕДОВАНИЯМИ. Тело цикла выполняется столько раз, сколько и весь цикл. Признаком ЦИКЛ-ПОКА является возможность не выполнения тела цикла ни разу. При равноценности из двух конструкций ЦИКЛ-ДО и ЦИКЛ-ПОКА выбирают ту, запись которой короче.

Вообще ЦИКЛ-ДО можно закодировать структурой ЦИКЛ-ПОКА, если в подготовке записать некоторые действия из тела цикла. Из ЦИКЛА-ДО получается ЦИКЛ-ПОКА при его охвате структурой АЛЬТЕРНАТИВА.

Порядок декомпозиции циклов:

1) набирается "пустой" текст оператора цикла;

2) записывается логическое условие продолжения ЦИКЛ-ПОКА или завершения ЦИКЛ-ДО (при этом выявляется переменная цикла);

3) декомпозируется то действие тела цикла, которое изменяет логическое условие до невыполнения условия ЦИКЛ-ПОКА или до выполнения условия ЦИКЛ-ДО;

4) детализируется СЛЕДОВАНИЕ "Подготовка цикла";

5) детализируется оставшееся действие тела цикла как СЛЕДОВАНИЕ;

6) проводится проверка информационной согласованности всех элементов цикла;

7) проводится проверка правильности работы цикла с помощью безмашинного расчета трассы выполнения тестов с трехкратным (или более), однократным выполнением цикла и вообще без выполнения.

В текстах программ может использоваться еще одна вычислительная структура — РЕКУРСИЯ. Признаком этой структуры является наличие рекурсивных формул и вычислений. Все, что делает рекурсия, можно реализовать при помощи циклов и массивов. Однако если язык программирования допускает рекурсию, то ее использование может сократить код программы. Рекурсия всегда очень тщательно комментируется.

Рассмотрим порядок работы по методике разработки структурированных алгоритмов на следующем примере. Пусть требуется разработать программу решения квадратного уравнения, которое имеет вид

ax² + bx + c = 0.

Работа по методике начинается с полного уяснения задачи. Этому помогает применение модели "черного ящика", разработка форм вводимой и выводимой информации программы (например, в виде макетов экрана), подготовка первичных тестовых примеров. Не существует для всего многообразия задач точный порядок выполнения этих действий. Данные действия часто приходится выполнять параллельно, переключаясь с действия на действие по мере исчерпания возможностей развития текущего действия и открытия возможностей развития очередного действия.

Первоначально алгоритм должен представлять одну типовую структуру СЛЕДОВАНИЕ (одно действие со смыслом выполнить все действия программы, например, программа начисления заработанной платы, но не программа начисления заработанной платы и/или решения квадратного уравнения).

Глядя на тесты и изображение модели "черного ящика" (см. рис. 5.3), детализируем весь алгоритм как одно СЛЕДОВАНИЕ (последовательно выполняемое действие) в порядке: а) предварительная запись смысла действия "черного ящика"; б) выходная и/или выводимая информация; в) входная и/или вводимая информация; г) определяется действие в "черном ящике" (одно предложение).

При разработке алгоритмов программ входная, промежуточная и выходная информации характеризуются структурой данных. Важным являются порядок размещения значений в массивах, имена и значения констант описания размерностей массива, имена и значения переменных, характеризующие текущие значения используемого размера массива, имя и порядок изменения переменной индекса текущего элемента массива. Форма вводимой и выводимой на экран или печать информации может быть показана макетами экранов или документов.

Первичные тестовые примеры должны включать как обычные, так и стрессовые наборы тестовых входных данных. Каждый стрессовый набор тестовых данных предназначен для выявления реакции в особых случаях. Например: неверных действий пользователя, деления на ноль, выхода значения за допустимые границы и т. д. Любой набор тестовых данных должен содержать описание результата.

Исследуя "черный ящик" применительно к решению квадратного уравнения, можем записать предварительный комментарий сути всех действий программы: "Программа решения квадратного уравнения вида a*x*x + b*x + c = 0".

Далее выясняется, что еще не выявлена выходная информация "черного ящика", поэтому необходимо перейти к подготовке тестов, что поможет продолжить работу с "черным ящиком". В данном конкретном случае подготовить тесты поможет анализ задачи.

Итак, пусть известна "школьная" формула решения квадратного уравнения вида ax² + bx + с = 0.

Известно также, что первоначально надо вычислить дискриминант уравнения D:

D = b² — 4ac.

Даже если забыли о случае отрицательности дискриминанта — ничего страшного нет. Записываем формулу решения:

Нам известно, что если D < 0, то из отрицательного числа нельзя извлекать квадратный корень. Поэтому вспоминаем, что при отрицательном дискриминанте нет корней. Еще обнаруживаем факт особого случая, которому соответствует факт при D = 0 наличия двух равных корней. Еще известно, что делить на ноль нельзя, а при a = 0 имеем именно этот случай. В этом случае исходное квадратное уравнение превращается в линейное уравнение:

bx + c = 0.

Решение получившегося уравнения будет следующим:

x = (—c)/b.

Это решение возможно лишь в случае a = 0 и (одновременно) b ≠ 0. В случае a = 0 и (одновременно) b = 0 и (одновременно) c ≠ 0 линейное уравнение не имеет решения.

Анализируя исходное уравнение, выясняем, что в случае a = 0 и (одновременно) b = 0 и (одновременно) c = 0 уравнение имеет бесчисленное множество решений (корни x1 и x2 — любые числа).

Составим наглядную таблицу правил решения квадратного уравнения (табл. 5.3).

Таблица 5.3

Наглядная таблица правил решения квадратного уравнения

В табл. 5.3 нет сочетаний значений, которые еще не выявлены. Теперь можно определить выходную информацию "черного ящика", которая выдается в пяти вариантах:

1) уравнение имеет бесчисленное множество решений (корни x1 и x2 — любые числа);

2) значения двух различных корней x1 и x2;

3) значения двух равных корней в виде x1 и дополняющей надписи о двух равных корнях;

4) надпись нет решения;

5) значение одного корня x1 с надписью, что уравнение является линейным.

Тип переменных, в которых размещаются выходные значения корней x1 и x2, — вещественный (Real). Теперь определяем входную информацию. Из исходного уравнения следует, что входной информацией являются значения трех коэффициентов a, b, c типа вещественный (Real). В ходе анализа формул было установлено, что значения трех коэффициентов a, b, c могут принимать любые значения, что было не очевидно до анализа формул решения уравнения (например, случай a = 0).

Имена переменных будут достаточно мнемоничны, если придерживаться принятых в математике обозначений.

Окончательный комментарий сути действий всей программы: "Программа решения квадратного уравнения a*x*x + b*x + c = 0 с произвольными значениями коэффициентов a, b, c типа вещественный". Факт произвольности значений коэффициентов a, b, c на этапе предварительного выявления сути действия "черного ящика" еще не был выявлен.

Наконец, готовим тестовые примеры.

Совокупность тестов для всех выявленных случаев решения квадратного уравнения:

1) при a = 0, b = 0, c = 0 бесчисленное множество решений (корни x1 и x2 — любые числа);

2) при a = 2, b = 3, c = —2 значения двух различных корней x1 = —2 и x2 = 0,5;

3) при a = 1, b = 4, c = 4 значения двух равных корней в виде x1 = x2 = —2 и вывод дополняющей надписи о двух равных корнях;

4) при а = 2, b = 5, с = 4 вывод надписи "нет решения";

5) при a = 0, b = 2, c = —8 значение одного корня x1 = 4 с надписью, что уравнение является линейным;

6) при a = 0, b = 0, c = 2 вывод надписи "нет решения". Теперь можно сразу написать фрагмент программы, соответствующий проделанной работе:

Program Kvadrat;

{ Программа решения квадратного уравнения

вида a*x*x + b*x + c = 0 с произвольными

значениями коэффициентов a, b, c типа

вещественный }

Uses

Crt, Dos;

Var

a, b, c: Real; {Коэффициенты квадратного уравнения}

xl, x2: Real; {Корни квадратного уравнения}

begin

end.

Путем компиляции фрагмента программы на компьютере можно проверить корректность синтаксиса. Теперь подготовим макет изображения экрана монитора (рис. 5.16). На макете изображения экрана монитора символами □ отмечены поля ввода информации, а символами — поля вывода информации.

Обычно выводимая на экран информация не содержит имен переменных, но в данном случае принятые в математике имена целесообразно отобразить на экране.

Макет изображения экрана монитора также является тестом. На основе первичных тестовых примеров и организации входной и выходной информации готовится или один тест, или несколько обобщающих тестов. Все составленные тесты для решения квадратного уравнения вошли в обобщающий тест.

Разработка наглядных тестов. Для простейшего алгоритма решения квадратного уравнения первичные тесты вместе с математическими формулами уже обладают наглядностью. Продолжим составление программы решения квадратного уравнения.

Первоначально нужно выполнить действия, определенные макетом изображения на экране монитора, так как для выполнения алгоритма решения квадратного уравнения необходимы исходные данные в виде коэффициентов a, b, c. Однако вводу должен предшествовать вывод информации, поясняющей назначение программы и суть очередной вводимой порции данных. Это предопределяет первичную детализацию одиночное СЛЕДОВАНИЕ в ЦЕПОЧКУ СЛЕДОВАНИЙ. Первичное одиночное СЛЕДОВАНИЕ не может содержать входной и выходной информации. Входная информация должна либо быть введена, либо присвоена. Выходная информация по завершении программы никого не интересует. Итак, ниже представлена цепочка последовательных действий.

Рис. 5.16. Макет изображения экрана монитора

ClrScr; {Очистка экрана}

{Вывод информации о назначении программы}

WriteLn ('Программа решения квадратного уравнения');

WriteLn ('вида а*x*x + b*x + с = 0 с произвольны',

'ми значениями');

WriteLn ('коэффициентов a, b, c типа вещественный');

WriteLn;

{Ввод значений коэффициентов a, b, c}

Write ('Укажите значение коэффициента а = ');

ReadLn (a); {Ввод а}

Write ('Укажите значение коэффициента b = ');

ReadLn (b); {Ввод b}

Write ('Укажите значение коэффициента с = ');

ReadLn (с); {Ввод с}

{ Вывод проверочно-протокольной информации

о введенных значениях коэффициентов a, b, c}

WriteLn;

WriteLn ('Решается квадратное уравнение');

WriteLn (а:10:4, '*x*x + ', b:10:4, '* x + ',

с:10:4, ' = 0:'); { Само решение квадратного уравнения }

WriteLn;

Write ('Для завершения программы нажмите');

WriteLn (' любую клавишу…');

Repeat until KeyPressed; { Цикл ожидания нажатия

любой клавиши }

Действие "Очистка экрана" — артефакт реализации, а не задачи, но насколько приятнее обозревать экран без "лишней информации". Также артефактом реализации явились два последних оператора, которые обеспечивают удобство просмотра результатов работы программы. При отсутствии этих операторов и нахождении в оболочке Turbo Pascal для просмотра результатов работы программы пришлось бы вручную переключиться в окно результатов.

Написание операторов WriteLn, Write, ReadLn не вызвало затруднений благодаря заранее подготовленному макету изображения экрана монитора.

Действие "Само решение квадратного уравнения" представлено комментарием и пустой строкой, отмечающей факт добавления действий в будущем. Это объясняется тем, что решение и вывод результатов решения многовариантны, а, следовательно, действие "Само решение квадратного уравнения" нельзя представить ЦЕПОЧКОЙ СЛЕДОВАНИЙ. Многовариантность предполагает управляющие структуры.

Уточняем комментарии, операторы вывода Write и WriteLn.

Проводим проверку информационной согласованности СЛЕДОВАНИЙ в цепочке. Убеждаемся, что все последующие действия обеспечены информацией, определенной предшествующими действиями, в конкретном случае — операторами ReadLn. Особое внимание обращаем на действия, использующие ранее определенную информацию. Это оператор

WriteLn (a:10:4, '*x*x + ', b:10:4, '*x + ', c: 10:4, ' = 0: ');

и будущее действие

{ Само решение квадратного уравнения }.

Убеждаемся, что к моменту их выполнения значения коэффициентов a, b, c уже определены. Теперь можно собрать реализованную часть программы и путем ее выполнения на тестах убедиться, что действия ввода и вывода введенной информации программы исполняются корректно.

Program Kvadrat;

{ Программа решения квадратного уравнения

вида а*х*х + Ь*х + с = 0 с произвольными значениями

коэффициентов а, Ь, с типа вещественный }

Uses

Crt, Dos;

Var

a, b, c: Real; {Коэффициенты квадратного уравнения}

xl, x2: Real; {Корни квадратного уравнения}

begin

ClrScr; {Очистка экрана}

{Вывод информации о значении программы}

WriteLn ('Программа решения квадратного уравнения');

Write (

'вида а*х*х + b*х + с = 0 с произвольными');

Write ('значениями');

WriteLn ('коэффициентов а, b, с типа вещественный');

WriteLn

{Ввод значений коэффициентов a, b, c}

Write ('Укажите значение коэффициента а = ');

ReadLn (a); { Ввод а}

Write ('Укажите значение коэффициента b = ');

ReadLn (b); { Ввод b}

Write ('Укажите значение коэффициента с = ');

ReadLn (c); { Ввод с}

{ Вывод проверочно-протокольной информации

о введенных значениях коэффициентов а, Ь, с }

WriteLn;

WriteLn ('Решается квадратное уравнение');

Write (a:10:4, '*x*x + ', b:10:4, '*x + ');

WriteLn (c:10:4, ' = 0: ');

{ Само решение квадратного уравнения }

WriteLn;

WriteLn ('Для завершения программы нажмите ',

'любую клавишу…');

repeat until KeyPressed; { Цикл ожидания нажатия

любой клавиши}

end.

При сборке программы пришлось осуществить перенос части оператора WriteLn на новую строку.

Теперь осуществляем декомпозицию действия "Само решение квадратного уравнения".

Многовариантность вычислений предполагает цепочку альтернатив. Анализируя математические формулы обобщающего теста, табл. 5.3 и состав наборов выходной информации, выявляем, что ЦЕПОЧКА АЛЬТЕРНАТИВ содержит четыре альтернативных действия. Строкам с 1-й по 3-ю табл. 5.3 соответствует одно действие, поскольку для их выполнения требуется уже вычисленное значение дискриминанта d. Записываем комментарий предшествующего СЛЕДОВАНИЯ всей ЦЕПОЧКИ АЛЬТЕРНАТИВ, набор входной информации (выходной информации — нет) и оформляем заготовку операторов ЦЕПОЧКИ АЛЬТЕРНАТИВ вместе с подчиненными СЛЕДОВАНИЯМИ:

Входная информация: a, b, c

{ Само решение квадратного уравнения }

if

then

begin

{ Продолжение решения с вычислением дискриминанта }

end;

if

then

begin

{ Решение линейного уравнения }

end;

if

then

begin

{ Ввод сообщения: линейное уравнение не имеет решения }

WriteLn ("Нет решения ')

end;

if

then

begin

{ Вывод сообщения: бесчисленное множество решений уравнения }

Write ('бесчисленное множество решений уравне');

WriteLn ('ния (корни — любые числа)');

end;

В последней альтернативе одна строка выводится одним оператором.

Далее в соответствии с действиями запишем логические условия выполнения действий. При этом простым сравнением проверять на равенство значения двух вещественных переменных нельзя. Например, при сравнении f = g, считающихся равными 5, даже если g = 5,00000, в силу округлений при вычислениях значение f может оказаться равным либо 4,99999, либо 5,00000, либо 5,00001. Согласно данному примеру путем простой проверки на равенство факт равенства будет установлен в одном случае из трех.

Для надежного сравнения двух вещественных чисел используют прием использования неравенства |f — g| ≤ ε, где ε — заведомо малое число. На языке программирования это неравенство имеет вид

Abs (f — g) <= 1е — 6

Продолжаем кодирование структуры. Глядя на действия, записываем логические условия выполнения действий. Входная информация: a, b, c.

{ Само решение квадратного уравнения }

if (Abs(а) > 1e — 6)

then

begin

{ Продолжение решения с вычислением дискриминанта }

end;

if ((Abs (a) <= 1e — 6) and (Abs (b) > 1e — 6))

then

begin

{ Решение линейного уравнения }

end;

if ((Abs(a) <= 1e — 6) and (Abs(b) <= 1e — 6 and (Abs(c) >

1e — 6))

then

begin

{ Вывод сообщения: линейное уравнение не имеет решения }

WriteLn ('Нет решения');

end;

if ((Abs(a) <= 1e — 6) and (Abs(b) <= 1e — 6 and

(Abs(c) <= 1e — 6))

then

begin

{ Вывод сообщения: бесчисленное множество решений уравнения }

Write ('бесчисленное множество решений уравне');

WriteLn ('ния (корни — любые числа)');

end;

Осуществим сборку получившейся программы. При сборке удалим избыточные комментарии и избыточные операторные скобки begin — end, охватывающие лишь один оператор. Испытаем полученную программу на тестах a = 0, b = 0, c = 0 a = 0, b = 0, c = 2. Собранный вариант программы:

Program Kvadrat;

{ Программа решения квадратного уравнения

вида a*x*x + b*x + c = 0 с произвольными значениями

коэффициентов a, b, c типа вещественный }

Uses

Crt, Dos;

Var

a, b, c: Real; {Коэффициенты квадратного уравнения}

xl, x2: Real; {Корни квадратного уравнения}

begin

ClrScr; { Очистка экрана }

{Вывод информации о назначении программы}

WriteLn ('Программа решения квадратного уравнения');

Write (

'вида a*x*x + b*x + c = 0 с произвольными');

Write ('значениями');

WriteLn ('коэффициентов a, b, c типа вещественный');

WriteLn;

{Ввод значений коэффициентов а, b, с};

Write ('Укажите значение коэффициента а = ');

ReadLn(a); { Ввод а}

Write ('Укажите значение коэффициента b = ');

ReadLn(b); { Ввод b}

Write ('Укажите значение коэффициента с = ');

ReadLn(c); { Ввод с}

{ Вывод проверочно-протокольной информации

о введенных значениях коэффициентов a, b, c }

WriteLn;

WriteLn ('Решается квадратное уравнение');

Write (a:10:4, '*x*x + ', b:10:4, '*x + ');

WriteLn(с:10:4, ' = 0:');

{ Само решение квадратного уравнения }

if (Abs (a) > 1e — 6)

then

begin

{ Продолжение решения с вычислением дискриминанта }

end;

if ((Abs(a) <= 1e — 6) and (Abs(b) > 1e — 6))

then

begin

{ Решение линейного уравнения }

end;

if ((Abs(a) <= 1e — 6) and (Abs(b) <= 1e — 6) and

(Abs(c) > 1e — 6))

then

WriteLn ('Нет решения');

if ((Abs(a) <= 1e — 6) and (Abs(b) <= 1e — 6 and

(Abs(c) <= 1e — 6))

then

begin

Write ('бесчисленное множество решений уравне');

WriteLn ('ния (корни — любые числа)');

end;

WriteLn;

Write ('Для завершения программы нажмите');

WriteLn ('любую клавишу…');

repeat until KeyPressed; { Цикл ожидания нажатия

любой клавиши }

end.

Декомпозируем действие "Решение линейного уравнения". Это действие представляет цепочку из двух элементарных операторов. Выполним проверку информационной согласованности действий:

Входная информация: b, с.

{ Решение линейного уравнения }

x1:= — c/b;

WriteLn ('уравнение линейное x = ', x1: 10: 4);

Декомпозируем действие "Продолжение решения с вычислением дискриминанта". Данное действие представляет ЦЕПОЧКУ СЛЕДОВАНИЙ из двух СЛЕДОВАНИЙ.

Входная информация: а, Ь, с

{ Продолжение решения с вычислением дискриминанта }

{ Вычисление дискриминанта квадратного уравнения }

d:= Sqr (b) — 4.0*а*с; { Решение уравнения }

Переменная d у нас не описана, поэтому в секцию Var необходимо добавить строку описания:

d: Real; { Значение дискриминанта }

Декомпозируем действие "Решение уравнения". Согласно табл. 5.3 данное действие представляет ЦЕПОЧКУ АЛЬТЕРНАТИВ из трех альтернатив в цепочке. Осуществив детализацию этих альтернатив в установленном порядке, получим:

Входная информация: a, b, c, d.

{ Решение уравнения }

if d > 1e-6

then

begin

{ Расчет двух различных корней }

end;

if ((d >= -1e-6) and (d <= 1e-6))

then

begin

{ Расчет двух равных корней }

WriteLn ('два равных корня x = ', (-b)/(2.0 * а):10:4);

end;

if d < -1e-6 then begin

{ Вывод надписи: уравнение не имеет решения }

WriteLn ('уравнение не имеет решения');

end;

Декомпозируем действие "Расчет двух различных корней". Это действие представляет цепочку из трех элементарных операторов. Выполним проверку информационной согласованности действий:

Входная информация: a, b, c, d

{ Расчет двух различных корней }

x1:= ((-b) — Sqrt (d))/(2.0*a);

x2:= ((-b) + Sqrt (d))/(2.0*а);

Write ('два различных корня x1 = ', x1:10:4);

WriteLn (' x2 = ', х2:10:4);

Здесь вывод одной строки осуществлен двумя операторами. Осуществим сборку всей программы, удалив избыточные комментарии и избыточные операторные скобки begin — end, охватывающие лишь один оператор. Испытаем полученную программу на всех заранее подготовленных тестах. Собранный вариант программы:

Program Kvadrat;

{ Программа решения квадратного уравнения

вида a*x*x + b*x + c = 0 с произвольными значениями

коэффициентов a, b, c типа вещественный }

Uses

Crt, Dos;

Var

a, b, c: Real; {Коэффициенты квадратного уравнения}

xl, x2: Real; {Корни квадратного уравнения}

dl: Real; {Значение дискриминанта}

begin

ClrScr; { Очистка экрана }

{Вывод информации о назначении программы}

WriteLn ('Программа решения квадратного уравнения');

WriteLn (

'вида a*x*x + b*x + c = 0 с произвольными', 'значениями');

WriteLn ('коэффициентов a, b, c типа ', 'вещественный');

WriteLn

{Ввод значений коэффициентов a, b, c}

Write ('Укажите значение коэффициента а = ');

ReadLn(a); { Ввод а }

Write ('Укажите значение коэффициента b = ');

ReadLn(b); { Ввод b}

Write ('Укажите значение коэффициента с = ');

ReadLn(c); { Ввод с }

{ Вывод проверочно-протокольной информации

о введенных значениях коэффициентов a, b, c }

WriteLn;

WriteLn ('Решается квадратное уравнение');

WriteLn (а:10:4, '*x*x + ', b:10:4, '*x + ',

с:10:4, ' = 0:');

{ Само решение квадратного уравнения }

if (Abs (a) > 1e-6)

then

begin

{ Продолжение решения с вычислением дискриминанта }

{ Вычисление дискриминанта квадратного уравнения }

d:= Sqr(b) — 4.0*а*с;

{ Решение уравнения }

if d > 1e-6

then

begin

{ Расчет двух различных корней }

x1:= (-b) — Sqrt(d)/(2.0*a);

х2:= (-b) + Sqrt(d)/(2.0*a);

Write ('два различных корня x1 = ',

x1:10:4);

WriteLn (' х2 = ', х2:10:4);

end;

if ((d >= -1e-6) and (d <= 1e-6))

then

WriteLn ('два равных корня х = ', (-b)/(2.0*a):10:4);

if d < -1e-6 then

WriteLn ('уравнение не имеет решения');

end;

if ((Abs(a) <= 1e-6) and (Abs(b) > 1e-6))

then

begin

{ Решение линейного уравнения }

x1:= — c/b;

WriteLn ('уравнение линейное х = ', x1:10:4);

end;

if ((Abs(a) <= 1e-6) and (Abs(b) <= 1e-6 and

(Abs(c) > 1e-6))

then

WriteLn ('Нет решения');

if ((Abs(a) <= 1e-6 and (Abs(b) <= 1e-6 and

(Abs(c) <= 1e-6))

then

begin

Write ('Бесчисленное множество решений',

'уравне');

WriteLn ('ния (корни — любые числа)');

end;

WriteLn;

Write ('Для завершения программы нажмите');

WriteLn ('любую клавишу…');

repeat until KeyPressed; { Цикл ожидания

нажатия любой клавиши }

end.

В качестве примера приводится учебная работа, выполненная одним из обучаемых. Работа была оформлена на отдельных листах формата A4. Курсивом выделены пояснения авторов учебника, которые были дополнительно ими внесены в текст работы.

Страница 1 (без нумерации) представляет собой титульный лист с наименованием: "ЗАДАНИЕ НА СОСТАВЛЕНИЕ СТРУКТУРИРОВАННОГО АЛГОРИТМА".

Страница 2 содержит постановку задачи и набор тестов, составленных до разработки алгоритма процесса.

Шаг 1. ПОСТАНОВКА ЗАДАЧИ

Составить алгоритм умножения двух положительных чисел с произвольным (до ста) количеством цифр. Цифры сомножителей и результата должны находиться в одномерных массивах. Разрядность результата не должна превышать 100 цифр.

Шаг 2. НАБОР ТЕСТОВ, СОСТАВЛЕННЫХ ДО РАЗРАБОТКИ АЛГОРИТМА ПРОЦЕССА

Пусть предельная разрядность сомножителей равна трем цифрам, а результата — четырем. Аналогично приведенному образцу умножения чисел 391*56 = 21896 (переполнение) были составлены тесты: 23*132 = 3036; 111*11 = 1221; 999*99 = 98901 (переполнение); 00*000 = 0; 1*0 = 0.

Алгоритм умножения обычно изучался в младших классах школы по маршрутному описанию процесса счета. Из-за теоретической огромности числа маршрутов большинство со школьной скамьи не знает процесса умножения при нулевых сомножителях!

Страница 3 содержит результаты анализа выходной и входной информации вычислительного процесса со структурами данных. Рациональность избранной структуры данных в значительной мере определяет рациональность алгоритма.

Шаг 3. АНАЛИЗ ВЫХОДНОЙ И ВХОДНОЙ ИНФОРМАЦИИ ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА

Анализ выходной и входной информации начинается с рассмотрения модели "черного" ящика, показанной на рис. 5.3.

Program MultNumbers;

{Расчет произведения двух чисел}

uses

Crt;

const

Digits = 100; {Число цифр в числах}

type

TNumber = record

D: array[1..Digits] of Byte;

{B D[1] находится младший разряд числа}

N: word; {Число разрядов в числе от 1 до Digits}

end;

var

C1: TNumber; {Первый сомножитель}

C2: TNumber; {Второй сомножитель}

R: TNumber; {Результат умножения}

Error: boolean; {True — ошибка переполнения}

Макет экрана со строками диалога программы приведен на рис. 5.17. Вместо трех последних строк возможен вывод: "Ошибка переполнения".

Страница 4 содержит наглядное изображение процесса преобразования входных данных обобщающего теста или тестов в выходные данные со всеми внутренними данными и/или трассу выполнения обобщающего теста или тестов. Обобщающий тест или тесты составляются на основе тестов страницы 2 и при минимальном количестве тестов охватывает все маршруты процесса вычислений. Наглядность изображения изменений всех данных способствует упрощению процесса разработки алгоритма. Рациональность избранной структуры данных в значительной мере определяет рациональность алгоритма.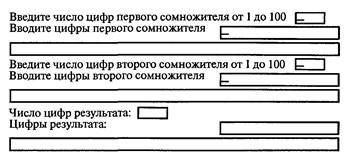

Рис. 5.17. Макет экрана со строками диалога программы

Шаг 4. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ ПРОЦЕССА ПРЕОБРАЗОВАНИЯ ВХОДНЫХ ДАННЫХ ОБОБЩАЮЩЕГО ТЕСТА В ВЫХОДНЫЕ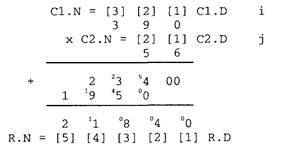

Вводим описание новых внутренних переменных:

var {Рабочие переменные}

i, j: word;

На первый взгляд, кажется, что необходимо ввести переменное количество промежуточных массивов (в зависимости от количества цифр второго сомножителя) для запоминания продукта умножения первого сомножителя на очередную цифру второго сомножителя. Однако внимательный анализ структур данных позволяет найти иной способ выполнения расчетов. При этом способе сначала обнуляется результат. Далее результат последовательно увеличивается на сдвинутый на разряд влево продукт умножения первого сомножителя на очередную цифру второго сомножителя. Переоформляем наглядное изображение процесса преобразования входных данных обобщающего теста.

На странице 4 или следующей иногда полезно поместить описание алгоритма в обыденном неструктурированном понимании.

Каждая последующая страница содержит результаты процесса детализации очередной выделенной от общего к частному структуры.

Шаг 5. ПОСЛЕДОВАТЕЛЬНОСТЬ ДЕТАЛИЗАЦИИ АЛГОРИТМА

Шаг 5.1. Результаты детализации СЛЕДОВАНИЯ "Вся программа"

Следование "Вся программа" детализируется ЦЕПОЧКОЙ СЛЕДОВАНИЙ:

begin

ClrScr; {Очистка экрана}

{Ввод корректного значения числа цифр первого сомножителя}

C1.N

Write('Вводите цифры первого сомножителя ');

{Ввод цифр первого сомножителя в порядке от C1.D[C1.N] до C1.D[1]}

C1.D

WriteLn;

{Ввод корректного значения числа цифр второго сомножителя}

С2.N

Write('Вводите цифры второго сомножителя ');

{Ввод цифр второго сомножителя в порядке от C2.D[C2.N] до C2.D[1]}

WriteLn;

{Расчет произведения сомножителей}

R.D R.N Error

{Устранение лидирующих нулей}

WriteLn;

{Вывод результата произведения}

WriteLn;

end.

Без отступов показана входная и выходная информация структур, которая использовалась при проверке информационной согласованности СЛЕДОВАНИЙ в ЦЕПОЧКЕ СЛЕДОВАНИЙ.

СЛЕДОВАНИЕ "Устранение лидирующих нулей" необходимо при использовании сомножителя, состоящего из нескольких нулей.

Шаг 5.2. Детализация СЛЕДОВАНИЯ "Ввод корректного значения числа цифр первого сомножителя"

СЛЕДОВАНИЕ "Ввод корректного значения числа цифр первого сомножителя" декомпозируется циклом:

{Ввод корректного значения числа цифр первого сомножителя}

repeat

Write('Введите число цифр первого сомножителя');

Write(' от 1 до ', Digits, ' ');

ReadLn(C1.N);

until ((C1.N >= 1) and (C1.N <= Digits));

Цикл оттестирован тремя тестами: C1.N=1; C1.N=3; C1.N=Digits.

Аналогично декомпозируется процесс "Ввод корректного значения числа цифр второго сомножителя".

Шаг 5.3. Детализация СЛЕДОВАНИЯ "Ввод цифр первого сомножителя в порядке от C1.D[C1.N] до C1.D[1]

СЛЕДОВАНИЕ "Ввод цифр первого сомножителя в порядке от C1.D[C1.N] до C1.D[1] декомпозируется циклом:

{Ввод цифр первого сомножителя в порядке от C1.D[C1.N] до C1.D[1]}

for i:= C1.N downto 1 do begin

{До ввода корректного символа цифры}

repeat

ch:= ReadKey; {Чтение символа клавиатуры}

Val(ch, C1.D[i], InCode); {Преобразование в значение}

until(InCode = 0);

Write(ch);

end;

Описания новых переменных:

var {Рабочие переменные}

InCode: word;

ch: Char;

Несмотря на то что здесь в нарушение правил детализировано сразу два цикла, в тестировании нет необходимости.

Аналогично декомпозируется процесс "Ввод цифр второго сомножителя в порядке от C2.D[C2.N] до C2.D[1].

Шаг 5.4. Детализация СЛЕДОВАНИЯ "Вывод результата произведения"

СЛЕДОВАНИЕ "Вывод результата произведения" декомпозируется АЛЬТЕРНАТИВОЙ — РАЗВИЛКА С ДВУМЯ ДЕЙСТВИЯМИ:

{Вывод результата произведения}

if ERROR

then

WriteLn(Ошибка переполнения)

else

begin

{Вывод продукта умножения}

end;

Тесты: ERROR = True; ERROR = False.

Шаг 5.5. Детализация СЛЕДОВАНИЯ "Вывод продукта умножения"

СЛЕДОВАНИЕ "Вывод продукта умножения" декомпозируется циклом:

{Вывод продукта умножения}

for i:= R.N downto 1 do

Write(R.D[i]);

В тестировании нет необходимости.

Шаг 5.6. Детализация СЛЕДОВАНИЯ "Устранение лидирующих нулей"

СЛЕДОВАНИЕ "Устранение лидирующих нулей" декомпозируется циклом:

{Устранение лидирующих нулей}

while ((R.N > 1) and (R.D[i] = 0)) do

Dec(R.N); {R.N:= R.N — 1}

В тестировании нет необходимости.

Шаг 5.7. Детализация СЛЕДОВАНИЯ "Расчет произведения сомножителей"

СЛЕДОВАНИЕ "Расчет произведения сомножителей" декомпозируется циклом:

Вход: C1, C2.

{Расчет произведения сомножителей}

{Цикл задает номер j очередной цифры второго сомножителя}

ERROR:= False;

j:= 1;

R.D[1]:= 0;

while ((j <= C2.N) and

(not(ERROR))) do

begin

{Увеличение результата на сдвинутый продукт умножения первого сомножителя на j-ю цифру второго сомножителя}

Inc(j); {j:= j + 1}

end;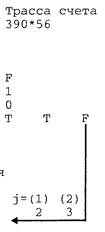

Выход: R.D, R.N, ERROR

Структура тестировалась на тестах: 390*56; 390*56, но при Digits = 5; 0*0 при C1.N = 0; 1*0 при C1.N = 1 и других тестах.

Шаг 5.8. Детализация СЛЕДОВАНИЯ "Увеличение результата на сдвинутый продукт умножения первого сомножителя на j-ю цифру второго сомножителя

СЛЕДОВАНИЕ детализируется циклом:

Вход: C1, C2.

{Увеличение результата на сдвинутый продукт умножения первого сомножителя на j-ю цифру второго сомножителя}

p:= 0;

i:= 0; {Номер цифры первого сомножителя}

while(((i < C1.N) or (p <> 0)) and (not(ERROR))) do

begin

Inc(i);

{Расчет очередной цифры результата и цифры переноса}

end;

Выход: R.D, R.N, ERROR

Шаг 5.9. Детализация СЛЕДОВАНИЯ "Расчет очередной цифры результата и цифры переноса"

СЛЕДОВАНИЕ детализируется альтернативой:

Вход: i, j, C1.D[i], C2.D[j], p, R.D, Digits.

{Расчет очередной цифры результата и цифры переноса}

{Контролируемый расчет ir — номера очередной цифры результата}

ir:= i + j — 1;

if (ir > Digits) then

ERROR:= True else

begin

{Изменение длины результата R.N}

if (R.N < ir)

then

begin

R.N:= ir;

R.D[ir]:= 0; {Обнуление новой цифры результата}

end;

{Получение очередной цифры C1D первого сомножителя}

if (i <= C1.N) then C1D:= C1.D[i] else C1D:= 0;

{Изменение очередной цифры результата и p}

RD:= р + R.D[ir] + C1D * С2.D[j];

R.D[ir]:= RD mod 10;

p:= RD div 10;

end;

Выход: R.D, R.N, ERROR, p.

Описания новых переменных:

var

ir, C1D, RD: word; {Рабочие переменные}

Шаг 6. РЕЗУЛЬТАТЫ СБОРКИ ПРОГРАММЫ

Program MultNumbers;

{Расчет произведения двух чисел}

uses

Crt;

const

Digits = 100; {Число цифр в числах}

type

TNumber = record

D: array[1..Digits] of Byte;

{BD[1] находится младший разряд числа}

N: word; {Число разрядов в числе от 1 до Digits}

end;

var

C1: TNumber; {Первый сомножитель}

C2: TNumber; {Второй сомножитель}

R: TNumber; {Результат умножения}

Error: boolean; {True — ошибка переполнения}

var

p: word; {Значение числа переноса при умножении C1.D на очередную цифру C2.D}

var {Рабочие переменные}

i, j, ir, C1D, RD, InCode: word;

ch: char; begin

ClrScr; {Очистка экрана}

{Ввод корректного значения числа цифр первого сомножителя}

repeat

Write('Введите число цифр первого сомножителя)

Write(' 1 до ', Digits, ' ');

ReadLn(C1.N);

until ((C1.N >= 1) and (C1.N <= Digits));

Write('Вводите цифры первого сомножителя ');

{Ввод цифр первого сомножителя в порядке от C1.D[C1.N] до C1.D[1]}

for i:= C1.N downto 1 do

begin

{До ввода корректного символа цифры}

repeat

ch:= ReadKey; {Чтение символа клавиатуры}

Val(ch, C1.D[i], InCode); {Преобразование в значение}

until(InCode = 0);

Write(ch);

end;

WriteLn;

{Ввод корректного значения числа цифр второго сомножителя}

repeat

Write('Введите число цифр второго сомножителя');

Write(' от 1 до ', Digits,' ');

ReadLn(C2.N);

until ((C2.N >= 1) and (C2.N <= Digits));

Write('Вводите цифры второго сомножителя ');

{Ввод цифр второго сомножителя в

порядке от C2.D[C2.N] до C2.D[1]}

for i:= C2.N downto 1 do

begin

{До ввода корректного символа цифры}

repeat

ch:= ReadKey; {Чтение символа клавиатуры}

Val(ch, C2.D[i], InCode); {Преобразование в

значение}

until(InCode = 0);

Write(ch);

end;

WriteLn;

{Расчет произведения сомножителей}

{Цикл задает номер j очередной цифры

второго сомножителя}

ERROR:= False;

j:= 1;

R.D[1]:= 0;

while ((j <= C2.N) and

(not(ERROR))) do

begin

{Увеличение результата на сдвинутый продукт умножения первого сомножителя на j-ю цифру второго сомножителя}

Р:= 0;

i:= 0; {Номер цифры первого сомножителя}

while(((i < C1.N) or (p <> 0)) and (not(ERROR))) do

begin

Inc(i);

{Расчет очередной цифры результата и цифры переноса}

{Контролируемый расчет ir — номера очередной цифры результата}

ir: = i + j — 1;

if (ir > Digits) then

ERROR:= True

else

begin

{Изменение длины результата R.N}

if (R.N < ir)

then

begin

R.N:= ir;

R.D[ir]:= 0; {Обнуление новой цифры результата}

end;

{Получение очередной цифры C1D первого

сомножителя}

if (i <= C1.N)

then

C1D:= C1.D[i]

else

C1D:= 0;

{Изменение очередной цифры результата и p}

RD:= p + R.D[ir] + C1D * C2.D[j];

R.D[ir]:= RD mod 10;

p:= RD div 10;

end;

end;

Inc(j); {j:= j + 1}

end;

{Устранение лидирующих нулей}

while ((R.N > 1) and (R.D[i] =0)) do

Dec(R.N); {R.N:= R.N — 1}

WriteLn;

{Вывод результата произведения}

if ERROR

then

WriteLn('Ошибка переполнения')

else

begin

{Вывод продукта умножения}

for i:= R.N downto 1 do

Write(R.D[i]);

end;

WriteLn;

end.

По окончании сборки программы имеет смысл еще раз отредактировать комментарии с изъятием "лишних" комментариев.

Пусть требуется разработать программу печати календаря заданного года на матричном принтере. Ограничимся годами после 1917 г. Матричный принтер может печатать информацию последовательно одна строка за другой.

Ниже представлен разработанный макет печати выходной информации. Из анализа макета стало очевидно, что входной информацией программы является только год выводимого на печать календаря. Разрабатываем макет экрана диалога программы.

Приступаем к разработке оперативной структуры данных программы. Что надо для печати календаря конкретного года? Конечно, можно создать статическую матрицу, содержащую все символы календаря, или статический вектор всех строк макета календаря. Попробуем обойтись без огромных массивов, формируя последовательно очередную строку информации.

Что видим? Информация дат месяца представлена на макете семью строками и шестью колонками дат месяцев. Что нужно для печати дат конкретного месяца? Количество пустых клеток дат в начале месяца и количество дней в месяце. Количество дней во всех месяцах года фиксировано, за исключением февраля. Количество дней в феврале зависит от того, является ли год високосным или нет. Итак, количество дней во всех месяцах года располагаем в статическом массиве.

Количество пустых клеток дат в начале следующего месяца определяется информацией предшествующего месяца. Эту информацию также располагаем в статическом массиве. Для заполнения статического массива количества пустых клеток дат в начале месяцев года необходимо знать информацию о количестве пустых клеток дат в начале января года печати календаря.

Количество пустых клеток дат в начале января года печати календаря можно определить исходя из количества пустых клеток дат в начале января 1917 г. с учетом выявленного из макета следующего факта, который состоит в том, что количество пустых клеток дат в начале января следующего года больше на 1 в невисокосный год и на 2 в високосный год.

Программа печати календаря заданного года

Укажите год распечатываемого календаря после 1917 года

(Не могу составить календарь  года

Для завершения программы нажмите любую клавишу…)

Ждите, идет печать…

Для завершения программы нажмите любую клавишу…

Нам требуется четыре строки наименований месяцев квартала и семь строк наименований дней недели. Эта информация остается неизменной в процессе выполнения программы, поэтому размещаем ее в константных массивах Turbo Pascal.

Итак, нам требуется многократно применяемое действие: определение, является ли исследуемый год високосным или нет. Оформляем это действие как функцию с возвращаемым результатом логического типа. Алгоритм данной функции возьмем из школьного учебника по астрономии.

Текст программы печати календаря на матричном принтере приведен ниже. Сверяясь с этим текстом, самостоятельно закодируйте программу.

Program Calendar;

{Программа печати календаря заданного года на матричном принтере.

Год должен быть начиная с YEARBASE года}

Uses

Crt, Dos;

Const

YEARBASE = 1917; {Начальный базовый год }

BLANKS1917 = 0; {Число пустых клеток в

начале января базового года}

KVARTALNAME: array [1…4] of String [53] =

({Константы укорочены при макетировании! }

'

Январь Февраль Март',

'

Апрель Май Июнь',

' Июль Август Сентябрь',

'

Октябрь Ноябрь Декабрь'

);

WEEKDAYNAME: Array [1…7] of String [2] =

('Пн', 'Вт', 'Ср', 'Чт', 'Пт', 'Сб', 'Вс');

Var

F: Text; {Файловая переменная}

Year: Word; {Год распечатываемого календаря}

Kvartal: Word; {Квартал года}

{Количество дней в каждом месяце}

MonthsDays: Array [1…12] of Word;

{Количество пустых клеток в начале января года Year}

Balnks: Word;

{Количество пустых клеток в начале каждого месяца }

BlanksDaus: Array [1…12] of Word;

idW: Word; {Номер дня недели }

iMonth: Word; {Номер месяца в году }

iKvartalMonth: Word; {Номер месяца в квартале }

iCol: Word; {Номер колонки в месяце квартала }

iCell: Word; {Номер клетки в месяце квартала}

i: Integer;

Function Vys (Year: Word): Boolean;

{Функция возвращает True в случае високосности

года Year}

begin

Vys: = False;

if (((Year mod 4 = 0) and (Year mod 100<>0))

or (Year mod 1000 = 0))

then

Vys: = True;

end; {Vys}

begin { Основная программа }

ClrScr; {Очистка экрана }

Write ('Программа печати календаря');

WriteLn ('заданного года');

Write ('Укажите год распечатываемого');

WriteLn ('календаря после', YEARBASE: 5, 'года');

ReadLn (Year);

{Контроль введенного года }

if Year < YEARBASE then

begin

{Аварийное завершение программы }

Write ('He могу составить календарь');

WriteLn (Year: 5, 'года');

Write ('Для завершения программы');

WriteLn ('нажмите любую клавишу…');

repeat until KeyPressed;

Halt (1);

end;

WriteLn ('Ждите, идет печать…');

Assign (F, 'PRN');

Rewrite (F);

{Печать календаря на принтере }

{Часть пробелов в следующей строке была изъята!}

WriteLn (F, ' ', Year);

{Подготовка информации}

{Определение количества пустых клеток в январе года Year}

Blanks: = BLANKS1917;

i:= YEARBASE;

while (I Year) do begin

{Увеличение Blanks}

Inc (Blanks); {В любой год плюс 1 }

if Vys (i)

then

Inc (Blanks); {Прошлый год високосный, +2}

{Корректировка Blanks}

if (Blanks >= 7) then Blanks:= Blanks — 7;

Inc (i); {Текущий год }

end;

{Определение количества дней в каждом месяце }

for i:= 1 to 12 do

MonthsDays [i]:= 31;

MonthsDays [4]:= 30;

MonthsDays [6]:= 30;

MonthsDays [9]:= 30;

MonthsDays [11]:= 30;

MonthsDays [2]:= 28;

if Vys (Year) then MonthsDays [2]: = 29;

{Определение количества пустых клеток в начале

каждого месяца }

BlanksDays [1]:= Blanks;

for i: = 2 to 12 do

if BlanksDays [i — 1] + MonthsDays [i — 1] < 35

then

BlanksDays [i]:= BlanksDays [i — 1] + MonthsDays [i — 1] — 28

else

BlanksDays [i]:= BlanksDays [i — 1] + MonthsDays [i — 1] — 35;

{Задание номеров кварталов }

{Печать тела календаря }

for Kvartal:= 1 to 4 do begin

{Печать наименования квартала }

WriteLn (F, KVARTALNAME [Kvartal]);

{Печать дат квартала }

{Задание номера дня недели }

for iDW:= 1 to 7 do

begin

{Печать наименования дней недель }

Write (f, WEEKDAYNAME [iDW];

{Печать трех месяцев дат квартала }

for iKvartalMonth: = 1 to 3 do begin

{Расчет номер месяца в квартале }

iMonth: = (Kvartal — 1) * 3 + iKvartalMonth;

{Печать шести колонок дат дня недели квартала}

for iCol:= 1 to 6 do begin

iCell:= (iCol — 1)*7 + iDW;

if ((iCell > BlanksDays [iMonth]) and (iCell <= BlanksDays [iMonth] +

MonthsDays [iMonth]))

then

Write (F, iCell — BlanksDays [iMonth]: 3)

else

Write (F, ' ');

end;

end;

{Печать наменования дней недель }

WriteLn (F, WEEKDAYNAME [iDW];

end;

end;

Close (F);

Write ('Для завершения программы');

WriteLn ('нажмите любую клавишу…');

Repeat until KeyPressed;

end.

ВЫВОДЫ

• С появлением ЭВМ актуальным стал поиск способов описания вычислительных алгоритмов. В 60-х годах уже применялись два способа описания алгоритмов: словесный пошаговый и графический в виде схем алгоритмов (жаргонно: блок-схем алгоритмов).

• Согласно современным технологиям программирования, описания алгоритмов в словесно пошаговой и графической формах, в виде схем алгоритмов практически не используются. Их заменили самодокументированные тексты, состоящие из стандартных структур кодирования.

• Хорошим функциональным описанием является описание безошибочное, однозначное для читателя, краткое, суть которого понимается быстро. Согласно проектной процедуре, хорошее функциональное описание составляется от общего к частному с использованием особых конструкций предложений — типовых элементов (типовых структур или просто структур).

• Любые алгоритмы или эвроритмы должны состоять только из стандартных структур. Каждая стандартная структура строго имеет один информационный вход и один информационный выход. Использование иных (нестандартных) структур приводит либо к удлинению описания, либо к невозможности тестирования (из-за нереально огромного объема необходимых тестов), либо к потере понятности.

• При разработке эвроритмов входная, промежуточная и выходная информации обычно характеризуются наименованиями предметов, их состоянием, местоположением и временем.

• При разработке алгоритмов программ входная, промежуточная и выходная информации характеризуются именами и набором значений как простых, так и структурированных переменных (записей, массивов).

• Первоначально алгоритм или эвроритм должен представлять одну типовую структуру СЛЕДОВАНИЕ (одно действие со смыслом "выполнить все действия программы"). Далее до достижения элементарных действий (элементарных операторов языка программирования или элементарных операций) отдельные структуры СЛЕДОВАНИЕ декомпозируются с соблюдением принципа от общего к частному одной из трех стандартных структур: ЦЕПОЧКА СЛЕДОВАНИЙ; ЦЕПОЧКА АЛЬТЕРНАТИВ; ПОВТОРЕНИЕ.

• Переход на новый язык программирования рекомендуется начинать с разработки стандарта кодирования типовых вычислительных структур.

• Алгоритм во многом определяется структурой данных.

• Тесты — необходимый атрибут разработки алгоритма.

• Обобщающий тест или тесты — минимальный набор тестовых данных, охватывающих все возможные случаи вычислений.

• Алгоритмы из старых книг лучше понимаются после их рефакторинга.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Перечислите основные недостатки каждого из способов описания алгоритмов.

2. Что такое функциональное описание?

3. Для чего предназначена проектная процедура разработки функциональных описаний?

4. Изложите требования к способу мышления пользователя проектной процедурой разработки функциональных описаний.

5. В каких случаях программисты могут применять проектную процедуру?

6. В каких случаях не программисты могут применять проектную процедуру?

7. Каковы основные характеристики структур СЛЕДОВАНИЕ, АЛЬТЕРНАТИВА и ПОВТОРЕНИЕ?

8. Каков порядок основных шагов (этапов) выполнения проектной процедуры?

9. Приведите пример описания внешних и внутренних данных программы.

10. Зачем нужна модель "черного ящика"?

11. Назовите тесты, разрабатываемые до программирования. Назначение. Содержание. Формы.

12. Назовите признаки структуры ЦЕПОЧКА СЛЕДОВАНИЙ.

13. Назовите порядок детализации одиночного СЛЕДОВАНИЯ.

14. Назовите порядок детализации ЦЕПОЧКИ СЛЕДОВАНИЙ.

15. Назовите признаки структур вида АЛЬТЕРНАТИВА.

16. Назовите порядок детализации ЦЕПОЧКИ АЛЬТЕРНАТИВ.

17. Запишите пример кодировки альтернатив с одним и двумя действиями.

18. Запишите пример кодировки альтернатив с тремя и более действиями.

19. Назовите признаки структуры ПОВТОРЕНИЕ.

20. Назовите порядок детализации структур универсальных циклов ДО и ПОКА.

21. Запишите пример кодировки структуры НЕУНИВЕРСАЛЬНЫЙ ЦИКЛ-ДО.

22. Запишите пример кодировки структур УНИВЕРСАЛЬНЫЕ ЦИКЛЫ ДО и ПОКА.

23. Как производится доказательство корректности алгоритмов при выполнении проектной процедуры.

24. Дополните описание процесса "Кипячение воды в чайнике" наглядными рисунками.