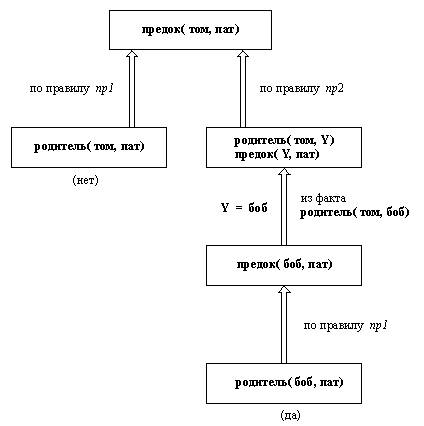
Назад | Содержание| Вперёд 1. 4. Как пролог-система отвечает навопросы...

Назад | Содержание| Вперёд

1. 4. Как пролог-система отвечает навопросы

В данном разделе приводится неформальноеобъяснение того, как пролог-системаотвечает на вопросы.

Вопрос к системе - это всегдапоследовательность, состоящая из одной илинескольких целей. Для того, чтобы ответить навопрос, система пытается достичь всех целей. Чтозначит достичь цели? Достичь цели - это значитпоказать, что утверждения, содержащиеся ввопросе, истинны в предположении, что всеотношения программы истинны. Другими словами,достичь цели - это значит показать, что она логически следует из фактов иправил программы. Если вопрос содержитпеременные, система должна к тому же найтиконкретные объекты, которые (будучиподставленными вместо переменных) обеспечиваютдостижение цели. Найденные конкретизациисообщаются пользователю. Если для некоторойконкретизации система не в состоянии вывестицель из остальных предложений программы, то ееответом на вопрос будет "нет".

Таким образом, подходящей интерпретациейпролог-программы в математических терминахбудет следующая: пролог-система рассматриваетфакты и правила в качестве множества аксиом, авопрос пользователя - как теорему; затем онапытается доказать эту теорему, т.е. показать, чтоее можно логически вывести из аксиом.

Проиллюстрируем этот подход на классическомпримере. Пусть имеются следующие аксиомы:

Все люди смертны.

Сократ - человек.

Теорема, логически вытекающая из этих двухаксиом:

Сократ смертен.

Первую из вышеуказанных аксиом можнопереписать так:

Для всех X, если X -человек, то X смертен.

Соответственно наш пример можно перевести наПролог следующим образом:

смертен( X) :- человек( X). % Все люди смертны

человек( сократ). % Сократ - человек

?- смертен( сократ). % Сократ смертен?

yes (да)

Более сложный пример из программы ородственных отношениях, приведенной на рис. 1.8:

?- предок( том, пат)

Мы знаем, что родитель( боб, пат) - этофакт. Используя этот факт и правило пр1, мыможем сделать вывод, что утверждение предок(боб, пат) истинно. Этот факт получен врезультате вывода - его нельзя найтинепосредственно в программе, но можно вывести,пользуясь содержащимися в ней фактами иправилами. Подобный шаг вывода можно короткозаписать

родитель( боб, пат) ==>предок( боб, пат)

Эту запись можно прочитать так: из родитель(боб, пат) следует предок( боб, пат)на основании правила пр1. Далее, нам известенфакт родитель( том, боб). На основанииэтого факта и выведенного факта предок( боб,пат) можно заключить, что, в силу правила пр2,наше целевое утверждение предок( том, пат)истинно. Весь процесс вывода, состоящий из двухшагов, можно записать так:

родитель(боб, пат) ==>предок( боб, пат)

родитель(том, боб) и предок( боб, пат) ==>

предок( том, пат)

Таким образом, мы показали, какой можетбыть последовательность шагов для достиженияцели, т.е. для демонстрации истинности целевогоутверждения. Назовем такую последовательностьцепочкой доказательства. Однако мы еще непоказали как пролог-система в действительностистроит такую цепочку.

Пролог-система строит цепочку доказательства впорядке, обратном по отношению к тому, которым мытолько что воспользовались. Вместо того, чтобыначинать с простых фактов, приведенных впрограмме, система начинает с целей и, применяяправила, подменяет текущие цели новыми, до техпор, пока эти новые цели не окажутся простымифактами. Если задан вопрос

?- предок( том, пат).

система попытается достичь этой цели. Для того,чтобы это сделать, она пробует найти такоепредложение в программе, из которого немедленноследует упомянутая цель. Очевидно, единственнымиподходящими для этого предложениями являются пр1и пр2.

Рис. 1. 11. Все шагидостижения цели предок( том, пат). Правая

ветвь демонстрирует, что цель достижима.

Графическое представление шагов вычисления нарис. 1.11 имеет форму дерева. Вершины деревасоответствуют целям или спискам целей, которыетребуется достичь. Дуги между вершинамисоответствуют применению (альтернативных)предложений программы, которые преобразуют цель,соответствующую одной вершине, в цель,соответствующую другой вершине. Корневая(верхняя) цель достигается тогда, когда находитсяпуть от корня дерева (верхней вершины) к еголисту, помеченному меткой "да". Листпомечается меткой "да", если он представляетсобой простой факт. Выполнение пролог-программысостоит в поиске таких путей. В процессе такогопоиска система может входить и в ветви,приводящие к неуспеху. В тот момент, когдаона обнаруживает, что ветвь не приводит к успеху,происходит автоматический возвратк предыдущей вершине, и далее следует попыткаприменить к ней альтернативное предложение.

Упражнение

1. 7. Постарайтесь понять, какпролог-система, используя программу, приведеннуюна рис. 1.8, выводит ответы на указанные нижевопросы. Попытайтесь нарисовать соответствующиедиаграммы вывода по типу тех, что изображены нарис.1.9 -1.11. Будут ли встречаться возвраты привыводе ответов на какие-либо из этих вопросов?

(a) ?- родитель( пам, боб).

(b) ?- мать(пам, боб).

(с) ?- родительродителя( пам, энн).

(d) ?- родительродителя( боб, джим).

Посмотреть ответ

Назад | Содержание| Вперёд

Оглавление