Назад | Содержание| Вперёд 14. 6. Работа с неопределенностью empty-...

Назад | Содержание| Вперёд

14. 6. Работа с неопределенностью

14. 6. 1. Степень достоверности

Наша оболочка экспертной системы, описанная впредыдущем разделе, может работать только стакими вопросами (утверждениями), которые либоистинны, либо ложны. Предметные области, вкоторых на любой вопрос можно ответить"правда" или "ложь", называются категорическими.Наши правила базы знания (также, как и данные)были категорическими, это были"категорические импликации". Однако многиеобласти экспертных знаний не являютсякатегорическими. Как правило, в заключенияхэксперта много догадок (впрочем, высказанных сбольшой уверенностью), которые обычно верны, номогут быть и исключения. Как данные,относящиеся к конкретной задаче, так иимпликации, содержащиеся в правилах, могутбыть не вполне определенными.Неопределенность можно промоделировать,приписывая утверждениям некоторыехарактеристики, отличные от "истина" и"ложь". Характеристики могут иметь своевнешнее выражение в форме дескрипторов, таких,как, например, верно, весьма вероятно, вероятно,маловероятно, невозможно. Другойспособ: степень уверенности может выражаться вформе действительного числа, заключенного внекотором интервале,например между 0 и 1 или между -5 и +5. Такую числовуюхарактеристику называют по-разному - "коэффициент определенности", "степень доверия" или "субъективнаяуверенность". Более естественным было быиспользовать вероятности (в математическомсмысле слова), но попытки применить их напрактике приводят к трудностям. Происходит этопо следующим причинам:

Экспертам, по-видимому, неудобно мыслить в терминах вероятностей. Их оценки правдоподобия не вполне соответствуют математическому определению вероятностей.

Работа с вероятностями, корректная с точки зрения математики, потребовала бы или какой-нибудь недоступной информации, или каких-либо упрощающих допущений, не вполне оправданных с точки зрения практического приложения.

Поэтому, даже если выбранная мераправдоподобия лежит в интервале 0 и 1, болееправильным будет называть ее из осторожности"субъективной уверенностью", подчеркиваяэтим, что имеется в виду оценка, данная экспертом.Оценки эксперта не удовлетворяют всемтребованиям теории вероятностей. Кроме того,вычисления над такими оценками могут отличатьсяот исчисления вероятностей. Но, несмотря на это,они могут служить вполне адекватной модельютого, как человек оценивает достоверность своихвыводов.

Для работы в условиях неопределенности былопридумано множество различных механизмов. Мыбудем рассматривать здесь механизм,используемый в системах Prospector и AL/X дляминералогической разведки и локализациинеисправностей соответственно. Следуетзаметить, что модель, применяемая всистеме Prospector, несовершенна как стеоретической, так и с практической точек зрения.Однако она использовалась на практике, онапроста и может служить хорошей иллюстрацией приизложении основных принципов, а потому вполнеподойдет нам, по крайней мере для первогознакомства с этой областью. С другой стороны,известно, что даже в значительно более сложныхмоделях не обходится без трудностей.

14. 6. 2. Модель Prospector'а

Достоверность событий моделируется с помощьюдействительных чисел, заключенных в интервалемежду 0 и 1. Для простоты изложения мы будемназывать их "вероятностями", хотя болееточный термин "субъективнаяуверенность". Отношения между событиями можнопредставить графически в форме "сетивывода". На рис. 14.14 показан пример сетивывода. События изображаются прямоугольниками, аотношения между ними - стрелками. Оваламиизображены комбинации событий (И, ИЛИ, НЕ).

Мы будем считать, что отношения между событиями(стрелки) являются своего рода "мягкимиимпликациями". Пусть имеются два события E и H, и пусть информация о том, чтоимело место событие Е, оказывает влияниена нашу уверенность в том, что произошло событие H. Если это влияние является "категорическойимпликацией", то можно просто написать

если Е то H

В случае же "мягкой импликации" этоотношение может быть менее определенным, так чтоему можно приписать некоторую "силу", скоторой оно действует:

если E то H с силой S

Та сила, с которой достоверность Е влияет на уверенность в H, моделируется всистеме Prospector при помощи двух параметров:

N = "коэффициент необходимости"

S = "коэффициент достаточности"

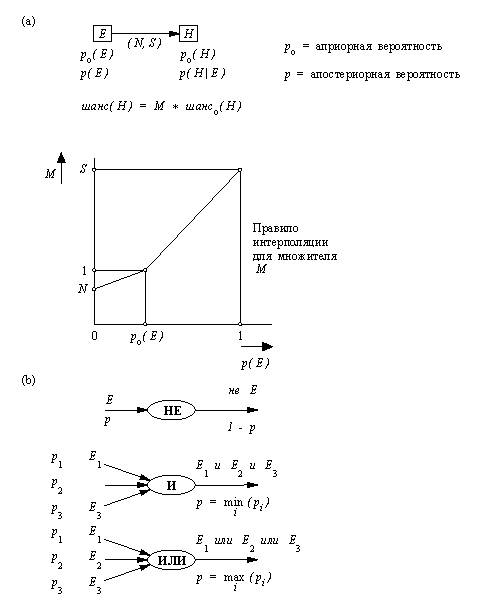
Рис. 14. 15. Правилараспространения вероятностей по сети,

принятые в системах Prospector и AL/X: (а) "мягкая импликация"

с силой (N, S); (b) логическиекомбинации отношений.

На рис. 14.15 показан один из способов реализацииэтого эффекта распространения информации посети. Часть вычислений производится не надвероятностями, а над шансами. Это удобно,хотя в принципе и не обязательно. Между шансами ивероятностями имеет место простое соотношение:

шанс = вер / ( 1 -вер)

вер = шанс / ( 1 + шанс)

Пусть между E и H существует отношение "мягкой импликации",тогда, в соответствии с рис. 14.15,

шанс (Н | Е) = М * шанс (H)

где множитель М определяется априорнойи апостериорной вероятностями с учетом силы ( N,S) связи между E и H. Предполагается, что правила Prospector'a (рис. 14.15) длявычисления вероятностей логических комбинацийсобытий (использующие min и max) правильномоделируют поведение человека при оценкесубъективной уверенности в таких составныхсобытиях.

14. 6. 3. Принципы реализации

Давайте сначала расширим правила языка, с темчтобы получить возможность работать снеопределенностью. К каждому, правилу мы можемдобавить "силовой модификатор",определяемый двумя неотрицательнымидействительными числами S и N. Вот соответствующий формат:

Имя Правила: если

Условие

то

Заключение

Сила( N, S).

Примеры правил рис. 14.14 можно изобразить в этойформе так:

прав1 : если

не давлоткр и

открклап

то

открклрано

сила( 0.001, 2000).

прав2 : если

сепзапвд

то

давлоткр

сила( 0.05, 400).

Для того, чтобы произвести соответствующеерасширение оболочки экспертной системы (разд.14.5), нам понадобится внести изменения вбольшинство процедур. Давайте сосредоточимсятолько на одной из них, а именно на процедуре

рассмотреть( Цель,Трасса, Ответ)

Мы предположим, что утверждение Цельне содержит переменных (как это сделано в Prospector'eи в AL/X). Это сильно упростит дело (особенно впроцедуре ответпольз). Таким образом, Цельбудет логической комбинацией элементарныхутверждений. Например:

не давлоткр иоткрклап

Цепочку целей-предков и правил Трассаможно представить таким же способом, как этосделано в разд. 14.5. Однако форму представленияобъекта Ответ придется модифицироватьдля того, чтобы включить в нее вероятности. Цель иее вероятность можно соединить в один термследующим образом:

Цель : Вероятность

Получим такой пример объекта Ответ:

индоткр : 1 былосказано

Смысл ответа: пользователь сообщил системе, чтособытие индоткр произошло, и что этоабсолютно достоверно.

Представление объекта Ответ требуетеще одной модификации, в связи с тем, что в одно ито же событие могут вести несколько независимыхсвязей, которые все окажут влияние навероятность этого события - его шанс будетпомножен (рис. 14.15) на все множители. В этом случае Ответбудет содержать список всех ветвей выводазаключения. Приведем пример ответа такого родадля сети рис. 14.14 (для наглядности расположенныйна нескольких строках):

давлоткр : 1 было'выведено по'

[ прав2 из сепзапвд : 1 было сказано,

прав5 из диагсеп : 1 было сказано ]

Процедура рассмотреть, выдающаяответы в такой форме, показана на рис. 14.16. Онаобращается к предикату

импликация( Р0, Р,Сила, Вер0, Вер)

соответствующему отношению "мягкойимпликации" (см. рис. 14.15). Р0 - априорная вероятность события Е, а Р - его апостериорная вероятность. Сила- сила импликации, представленная как

сила( N, S)

Вер0 и Вер - соответственноаприорная и апостериорная вероятности гипотезы H.

Следует заметить, что наша реализация оченьпроста, она обеспечивает только изменениевероятностей при распространении информации посети вывода и иногда ведет себя недостаточноразумно. Никакого внимания не уделяется отборудля анализа наиболее важной в данный моментинформации. В более сложной версии следовало бынаправлять процесс поиска ответа в сторонунаиболее существенных фактов. Кроме того,необходимо стремиться к тому, чтобы пользователюзадавалось как можно меньше вопросов.

Наконец, несколько замечаний относительноновой версии процедуры ответпольз. Онабудет проще, чем процедура рис. 14.11, так как взапросах, передаваемых пользователю, уже небудет переменных. На этот раз пользователь вкачестве ответа введет некоторую вероятность(вместо "да" или "нет"). Еслипользователю ничего неизвестно о событии,содержащемся в вопросе, то вероятность этогособытия не изменится. Пользователь может такжезадать вопрос "почему" и получитьизображение объекта Трасса в качествеобъяснения. Кроме того, следует разрешитьпользователю задавать вопрос: "Какова текущаявероятность моей гипотезы?" Тогда, если онустал вводить новую информацию (или у него маловремени), он может прекратить консультационныйсеанс, довольствуясь ответом системы, полученнымна основании неполной информации.

% Процедура

% рассмотреть( Цель, Трасса, Ответ)

% находит степень правдоподобия утверждения"цель это правда".

% Оценка правдоподобия содержится в объектеОтвет. Трасса - это

% цепочка целей-предшественников и правил,которую можно

% использовать в объяснении типа "почему"

рассмотреть( Цель,Трасса, ( Цель: Вер) было

'выведено по' ПравОтв) :-

bagof( Прав: если Условие то Цель с Сила, Правила),

% Все правила, относящиеся к цели

априори( Цель, Вер0),

% Априорная вероятность цели

модиф( Вер0, Правила, Трасса, Вер, ПравОтв).

% Модифицировать априорные вероятности

рассмотреть( Цель1 иЦель2, Трасса,

( Цель1 и Цель2 : Вер было 'выведено из'

( Ответ1 и Ответ2) ) :-

рассмотреть( Цель1, Трасса, Ответ1),

рассмотреть( Цель2, Трасса, Ответ2),

вероятность( Ответ1, В1),

вероятность( Ответ2, В2),

мин( В1, В2, Вер).

рассмотреть( Цель1или Цель2, Трасса,

( Цель или Цель2:Вер) было 'выведено из'

( Ответ1 и Ответ2) ) :-

рассмотреть( Цель1, Трасса, Ответ1),

рассмотреть( Цель2, Трасса, Ответ2),

вероятность( Ответ1, В1),

вероятность( Ответ2, В2),

макс( В1, В2, Вер).

рассмотреть( неЦель, Трасса,

( не Цель:Вер) было 'выведено из' Ответ) :-

рассмотреть( Цель, Трасса, Ответ),

вероятность( Ответ, В),

обратить( В, Вер).

рассмотреть( Цель,Трасса, ( Цель: Вер) было сказано) :-

ответпольз( Цель, Трасса, Вер).

% Ответ, выведенный пользователем

% Отношение

% модиф( Вер0, Правила, Трасса, Вер, ПравОтв)

% Существует Цель с априорной вероятностью Вер0.Правила имеют

% отношение к утверждению Цель; суммарное влияниеэтих правил

% (точнее, их условных частей) на Вер0 приводит ктому,

% что Вер0 заменяется на апостериорнуювероятность Вер;

% Трасса - список целей-предков и правил,использовавшихся

% при выводе утверждения Цель;

% ПравОтв - результаты анализа условных частей

% правил из списка Правила.

модиф( Вер0, [ ],Трасса, Вер0, [ ]).

% Нет правил - нет модификации

модиф( Вер0,

[ Прав : если Усл то Цель с Сила | Правила],

Трасса, Вер, [Прав из Ответ | ПравОтв] ):-

рассмотреть( Усл, [Цель по Прав | Трасса], Ответ),

% Условие из первого правила

априори( Усл, В0),

вероятность( Ответ, В),

импликация( В0, В, Сила, Вер0, Вер1),

% "Мягкая" импликация

модиф( Вер1, Правила, Трасса, Вер, ПравОтв).

Рис. 14. 16. Определениестепени правдоподобия гипотезы при помощи

распространения информации об оценкеуверенности по сети вывода.

Назад | Содержание| Вперёд

Оглавление