Назад | Содержание| Вперёд 13. 4. Поиск с предпочтением вИ / ИЛИ-графах...

Назад | Содержание| Вперёд

13. 4. Поиск с предпочтением вИ / ИЛИ-графах

13. 4. 1. Эвристические оценки иалгоритм поиска

Базовые процедуры поиска предыдущего разделапроизводят систематический и полный просмотр И /ИЛИ-дерева, не руководствуясь при этомкакими-либо эвристиками. Для сложных задачподобные процедуры весьма не эффективны из-забольшой комбинаторной сложности пространствапоиска. В связи с этим возникает необходимость вэвристическом управлении поиском, направленномна уменьшение комбинаторной сложности за счетисключения бесполезных альтернатив. Управлениеэвристиками, излагаемое в настоящем разделе,будет основано на численных эвристическихоценках "трудности" задач, входящих в составИ / ИЛИ-графа. Программу, которую мы составим,можно рассматривать как обобщение программыпоиска с предпочтением в пространстве состоянийгл. 12.

Начнем с того, что сформулируем критерийоптимальности, основанный на стоимостях дуг И /ИЛИ-графа. Во-первых, мы расширим нашепредставление И / ИЛИ-графов, дополнив егостоимостями дуг. Например, И / ИЛИ-граф рис. 13.4можно представить следующими предложениями:

а ---> или : [b/1, с/3].

b ---> и : [d/1, е/1].

с ---> и : [f/2, g/1].

e ---> или : [h/6].

f ---> или : [h/2, i/3].

цель( d). цель( g). цель( h).

Стоимость решающего дерева мы определим каксумму стоимостей его дуг. Цель оптимизации -найти решающее дерево минимальной стоимости. Каки раньше, иллюстрацией служит рис. 13.4.

Будет полезным определить стоимость вершиныИ / ИЛИ-графа как стоимость оптимальногорешающего дерева для этой вершины. Стоимостьвершины, определенная таким образом,соответствует "трудности" соответствующейзадачи.

Мы будем предполагать, что стоимости вершин И /ИЛИ-графа можно оценить (не зная соответствующихрешающих деревьев) при помощи эвристическойфункции h. Эти оценки будутиспользоваться для управления поиском. Нашапрограмма поиска начнет свою работу со стартовойвершины и, распространяя поиск из ужепросмотренных вершин на их преемников, будетпостепенно наращивать дерево поиска. Этотпроцесс будет строить дерево даже в том случае,когда сам И / ИЛИ-граф не является деревом; приэтом граф будет разворачиваться в дерево за счетдублирования своих отдельных частей.

Для продолжения поиска будет всегда выбираться"наиболее перспективное" решающеедерево-кандидат. Каким же образом используетсяфункция h для оценки степениперспективности решающего дерева-кандидата или,точнее, вершины-кандидата - корня этого дерева?

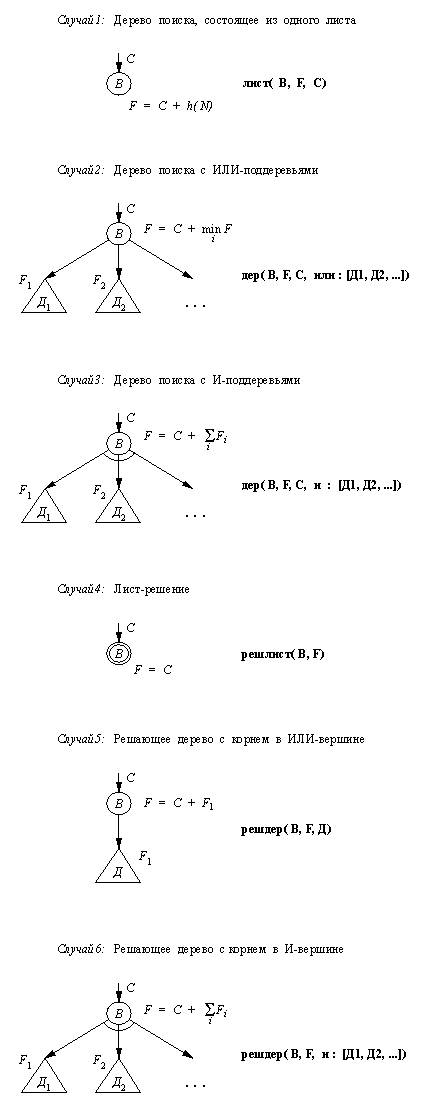
Рис. 13. 11. Представлениедерева поиска.

можностей имеется в виду. Это может быть одна изследующих комбинаций:

лист решлист дер решдер

Далее, в представление дерева входят все илинекоторые из следующих объектов:

корневая вершина дерева,

F-оценка дерева,

стоимость С дуги И / ИЛИ-графа, ведущей в корень дерева,

список поддеревьев,

отношение (И или ИЛИ) между поддеревьями.

Список поддеревьев всегда упорядочен повозрастанию F-оценок. Поддеревья,являющиеся решающими деревьями, помещаются вконец списка.

Обратимся теперь к программе рис. 13.12. Отношениесамого высокого уровня - это

и_или( Верш, РешДер)

где Верш - стартовая вершина.Программа строит решающее дерево (если таковоесуществует), рассчитывая на то, что оно окажетсяоптимальным решением. Будет ли это решение вдействительности самым дешевым, зависитот той функции h, которую используеталгоритм. Существует теорема, в которойговорится о том, как оптимальность решениязависит от h. Эта теоремааналогична теореме о допустимости алгоритмапоиска с предпочтением в пространстве состояний(гл. 12). Обозначим через С( В) стоимостьоптимального решающего дерева для вершины В. Если для каждой вершины В И /ИЛИ-графа эвристическая оценка h( B) <= C( B), то гарантируется, что процедура и_или найдет оптимальное решение. Если же h не удовлетворяет этому условию, то найденноерешение может оказаться субоптимальным.Существует тривиальная эвристическая функция,удовлетворяющая условию оптимальности, а именно h = 0 для всех вершин. Ее недостаткомявляется отсутствие эвристической силы.

Основную роль в программе рис. 13.12 играетотношение

расширить( Дер,Предел, Дер1, ЕстьРеш)

Дер и Предел - его"входные" аргументы, а Дер1 и ЕстьРеш- "выходные". Аргументы имеют следующийсмысл:

Дер - дерево поиска, подлежащеерасширению.

Предел - предельное значени F-оценки,при котором еще разрешено наращивать дерево Дер.

ЕстьРеш - индикатор, значения которогоуказывают на то, какой из следующих трех случаевимеет место:

(1) ЕстьРеш= да: Дер можно "нарастить" (сучетом ограничения Предел) такимобразом, чтобы образовалось решающее дерево Дер1.

(2) ЕстьРеш= нет: дерево Дер можно расширить досостояния Дер1, для которого F-оценкапревосходит Предел, но прежде чем F-оценкапревзошла Предел, решающее дерево небыло обнаружено.

(3) ЕстьРеш= никогда: Дер не содержит решения.

В зависимости от случая Дер1 - это либорешающее дерево, либо Дер, расширенноедо момента перехода через Предел; если ЕстьРеш= никогда, то переменная Дер1неинициализирована.

Процедура

расширспис(Деревья, Предел, Деревья1, ЕстьРеш)

аналогична процедуре расширить. Также, как и в процедуре расширить, Пределзадает ограничение на рост дерева, а ЕстьРеш- это индикатор, указывающий, каков результатрасширения ("да", "нет" или"никогда"). Первый аргумент - это, на этот раз,список деревьев (И-список или ИЛИ-список):

Деревья = или:[Д1, Д2,...] или

Деревья = и : [Д1, Д2, ...]

Процедура расширспис выбирает изсписка Деревья наиболее перспективноедерево (исходя из F-оценок). Так как деревья всписке упорядочены, таким деревом являетсяпервый элемент списка. Наиболее перспективноедерево подвергается расширению с новымограничением Предел1. Значение Предел1зависит от Предел, а также от другихдеревьев списка. Если Деревья - этоИЛИ-список, то Предел1 устанавливаетсякак наименьшая из двух величин: Предел иF-оценка следующего по "качеству"дерева из списка Деревья. Если Деревья- это И-дерево, то Предел1устанавливается равным Предел минуссумма F-оценок всех остальных деревьев изсписка. Значение переменной Деревья1зависит от случая, задаваемого индикатором ЕстьРеш.Если ЕстьРеш = нет, то Деревья1 -это то же самое, что и список Деревья,причем наиболее перспективное дерево расширенос учетом ограничения Предел1. Если ЕстьРеш= да, то Деревья1 - это решение длявсего списка Деревья (найденное безвыхода за границы значения Предел). ЕслиЕстьРеш = никогда, то переменная Деревья1неинициализирована.

Процедура продолжить, вызываемаяпосле расширения списка деревьев, решает, чтоделать дальше, в зависимости от результатасрабатывания процедуры расширить. Этапроцедура либо строит решающее дерево, либоуточняет дерево поиска и продолжает процесс егонаращивания, либо выдает сообщение"никогда" в случае, когда было обнаружено,что список деревьев не содержит решения.

/* ПРОГРАММА И / ИЛИ-ПОИСКА СПРЕДПОЧТЕНИЕМ

Эта программа порождает только однорешение. Гарантируется, что это решение самоедешевое при условии, что используемаяэвристическая функция является нижней граньюреальной стоимости решающих деревьев.

Дерево поиска имеет одну из следующих форм:

дер( Верш, F, С, Поддеревья) дерево-кандидат

лист( Верш, F, C) лист дерева поиска

решдер( Верш, F, Поддеревья) решающее дерево

решлист( Верш, F) лист решающего дерева

С - стоимость дуги, ведущей в Верш

F = С + Н, где Н - эвристическая оценка оптимальногорешающего дерева с корнем Верш

Список Поддеревья упорядочен такимобразом, что

(1) решающие поддеревьянаходятся в конце списка;

(2) остальные поддеревьярасположены в порядке возрастания F-оценок

:- ор( 500, xfx, :).

:- ор( 600, xfx, --->).

и_или( Верш, РешДер):-

расширить( лист( Верш, 0, 0), 9999, РешДер, да).

% Предполагается, что 9999 > любойF-оценки

% Процедура расширить( Дер, Предел, НовДер,ЕстьРеш)

% расширяет Дер в пределах ограничения Предел

% и порождает НовДер с "решающим статусом"ЕстьРеш.

% Случай 1: выход за ограничение

расширить( Дер,Предел, Дер, нет) :-

f( Дер, F), F > Предел, !. % Выход за ограничение

% В остальных случаях F <= Предел

% Случай 2: встретилась целевая вершина

расширить( лист(Верш, F, С), _, решлист( Верш, F), да) : -

цель( Верш), !.

% Случай 3: порождение преемников листа

расширить( лист(Верш, F,C), Предел, НовДер, ЕстьРеш) :-

расшлист( Верш, С, Дер1), !,

расширить( Дер1, Предел, НовДер, ЕстьРеш);

ЕстьРеш = никогда, !. % Нет преемников, тупик

% Случай 4: расширить дерево

расширить( дер( Верш, F, С, Поддеревья),

Предел, НовДер, ЕстьРеш) :-

Предел1 is Предел - С,

расширспис( Поддеревья, Предел1, НовПоддер,ЕстьРеш1),

продолжить( ЕстьРеш1, Верш, С, НовПоддер, Предел,

НовДер, ЕстьРеш).

% расширспис( Деревья, Предел, Деревья1,ЕстьРеш)

% расширяет деревья из заданного списка с учетом

% ограничения Предел и выдает новый списокДеревья1

% с "решающим статусом" ЕстьРеш.

расширспис(Деревья, Предел, Деревья1, ЕстьРеш) :-

выбор( Деревья, Дер, ОстДер, Предел, Предел1),

расширить( Дер, Предел1, НовДер, ЕстьРеш1),

собрать( ОстДер, НовДер, ЕстьРеш1, Деревья1,ЕстьРеш).

% "продолжить" решает, что делать послерасширения

% списка деревьев

продолжить( да,Верш, С, Поддеревья, _,

решдер( Верш, F, Поддеревья), да): -

оценка( Поддеревья, Н), F is С + H, !.

продолжить(никогда, _, _, _, _, _, никогда) :- !.

продолжить( нет,Верш, С, Поддеревья, Предел,

НовДер, ЕстьРеш) :-

оценка( Поддеревья, Н), F is С + Н, !,

расширить( дер( Верш, F, С, Поддеревья), Предел,

НовДер, ЕстьРеш).

% "собрать" соединяет результатрасширения дерева со списком деревьев

собрать( или : _, Дер,да, Дер, да):- !. % Есть решениеИЛИ-списка

собрать( или : ДД,Дер, нет, или : НовДД, нет) :-

встав( Дер, ДД, НовДД), !. % Нет решения ИЛИ-списка

собрать( или : [ ], _,никогда, _, никогда) :- !.

% Больше неткандидатов

собрать( или:ДД, _,никогда, или:ДД, нет) :- !.

% Есть ещекандидаты

собрать( и : ДД, Дер,да, и : [Дер Э ДД], да ) :-

всереш( ДД), !. % Есть решение И-списка

собрать( и : _, _,никогда, _, никогда) :- !.

% Нет решенияИ-списка

собрать( и : ДД, Дер,ДаНет, и : НовДД, нет) :-

встав( Дер, ДД, НовДД), !. % Пока нет решения И-списка

% "расшлист" формирует дерево извершины и ее преемников

расшлист( Верш, С,дер( Верш, F, С, Оп : Поддеревья)) :-

Верш---> Оп : Преемники,

оценить( Преемники, Поддеревья),

оценка( Оп : Поддеревья, Н), F is С + Н.

оценить( [ ], [ ]).

оценить( [Верш/С |ВершиныСтоим], Деревья) :-

h( Верш, Н), F is С + Н,

оценить( ВершиныСтоим, Деревья1),

встав( лист( Верш, F, С), Деревья1, Деревья).

% "всереш" проверяет, все ли деревья всписке "решены"

всереш([ ]).

всереш( [Дер |Деревья] ) :-

реш( Дер),

всереш( Деревья).

реш( решдер( _, _, _ ) ).

реш( решлист( _ , _) ).

f( Дер, F) :- % Извлечь F-оценку дерева

arg( 2, Дер, F), !. % F - это 2-й аргумент Дер

% встав( Дер, ДД, НовДД) вставляет Дер всписок

% деревьев ДД; результат - НовДД

встав( Д, [ ], [Д] ) :- !.

встав( Д, [Д1 | ДД], [Д,Д1 | ДД] ) :-

реш( Д1), !.

встав( Д, [Д1 | ДД], [Д1 |ДД1] ) :-

реш( Д),

встав( Д, ДД, ДД1), !.

встав( Д, [Д1 | ДД], [Д,Д1 | ДД] ) :-

f( Д, F), f( Д1, F1), F=< F1, !.

встав( Д, [Д1 | ДД], [ Д1| ДД1] ) :-

встав( Д, ДД, ДД1).

% "оценка" находит "возвращенную"F-оценку И / ИЛИ-списка деревьев

оценка( или :[Дер | _ ],F) :-

% Первое дерево ИЛИ-списка - наилучшее

f( Дер, F), !.

оценка( и :[ ], 0) :- !.

оценка( и : [Дер1 | ДД],F) :-

f( Дер1, F1),

оценка( и : ДД, F2),

F is F1 + F2, !.

оценка( Дер, F) :-

f( Дер, F).

% Отношение выбор( Деревья, Лучшее,Остальные, Предел, Предел1):

% Остальные - И / ИЛИ-список Деревья без его"лучшего" дерева

% Лучшее; Предел - ограничение для Списка Деревья,Предел1 -

% ограничение для дерева Лучшее

выбор( Оп : [Дер], Дер,Оп : [ ], Предел, Предел) :- !.

% Только один кандидат

выбор( Оп : [Дер | ДД],Дер, Оп : ДД, Предел, Предел1) :-

оценка( Оп : ДД, F),

( Оп = или, !, мин( Предел, F, Предел1);

Оп = и, Предел1 is Предел - F).

мин( А, В, А) :- А < В, !.

мин( А, В, В).

Рис. 13. 12. Программапоиска с предпочтением в И / ИЛИ-графе.

Еще одна процедура

собрать( ОстДер,НовДер, ЕстьРеш1, НовДеревья, ЕстьРеш)

связывает между собой несколько объектов, скоторыми работает расширспис. НовДер- это расширенное дерево, взятое из спискадеревьев процедуры расширспис, ОстДер- остальные, не измененные деревья из этогосписка, а ЕстьРеш1 указывает на"решающий статус" дерева НовДер.Процедура собрать имеет дело снесколькими случаями в зависимости от значения ЕстьРеш1,а также от того, является ли список деревьевИ-списком или ИЛИ-списком. Например, предложение

собрать( или : _, Дер,да, Дер, да).

означает: в случае, когда список деревьев - этоИЛИ-список и при только что проведенномрасширении получено решающее дерево, считать,что задача, соответствующая всему спискудеревьев, также решена, а ее решающее дерево иесть само дерево Дер. Остальные случаилегко понять из текста процедуры собрать.

Для отображения решающего дерева можноопределить процедуру, аналогичную процедуре отобр(рис. 13.8). Оставляем это читателю в качествеупражнения

13. 4. 3. Пример отношений,определяющих конкретную задачу: поиск маршрута

Давайте теперь сформулируем задачу нахождениямаршрута как задачу поиска в И / ИЛИ-графе, причемсделаем это таким образом, чтобы нашаформулировка могла бы быть непосредственноиспользована процедурой и_или рис. 13.12.Мы условимся, что карта дорог будет представленапри помощи отношения

связь( Гор1, Гор2, Р)

означающего, что между городами Гор1 и Гор2существует непосредственная связь, асоответствующее расстояние равно Р. Далее, мы допустим, что существует отношение

клпункт( Гор1-Гор2,Гор3)

имеющее следующий смысл: для того, чтобы найтимаршрут из Гор1 в Гор2, следуетрассмотреть пути, проходящие через Гор3( Гор3 - это "ключевой пункт" между Гор1и Гор2). Например, на карте рис. 13.1 f и g - это ключевые пункты между а и z:

клпункт( a-z, f). клпункт( a-z, g).

Мы реализуем следующий принцип построениямаршрута:

Для того, чтобы найти маршрут между городами X и Z, необходимо:

(1) если между X и Z имеются ключевые пункты Y1, Y2, ..., то найти один из путей:

путь из X в Z через Y1, или

путь из X в Z через Y2, или

...

(2) если между X и Z нет ключевых пунктов, то найтитакой соседний с X город Y, чтосуществует маршрут из Y в Z.

Таким образом, мы имеем два вида задач, которыемы будем представлять как

(1) X-Z найти маршрут из X в Z

(2) X-Z черезY найти маршрут из X в Z, проходящийчерез Y

Здесь 'через' - это инфиксный оператор болеевысокого приоритета, чем '-', и более низкого, чем'--->'. Теперь можно определить соответствующий И/ ИЛИ-граф явным образом при помощи следующегофрагмента программы:

:- ор( 560, xfx, через)

% Правила задачи X-Z,когда между X и Z

% имеются ключевыепункты,

% стоимости всех дугравны 0

X-Z ---> или :СписокЗадач

:- bagof( ( X-Z через Y)/0,клпункт( X-Z, Y),

СписокЗадач), !.

% Правила для задачиX-Z без ключевых пунктов

X-Z ---> или :СписокЗадач

:- bagof( ( Y-Z)/P, связь( X,Y, Р), СписокЗадач).

% Сведение задачитипа ''через" к подзадачам,

% связаннымотношением И

X-Z через Y---> и : [(X-Y)/0, ( Y-Z)/0].

цель( Х-Х) % Тривиальная задача:попасть из X в X

Функцию h можно определить,например, как расстояние, которое нужнопреодолеть при воздушном сообщении междугородами.

Упражнение

13. 4. Напишите процедуру

отобр2( РешДер)

для отображения решающего дерева, найденногопрограммой и_или рис. 13.12. Форматотображения пусть будет аналогичен тому, чтоприменялся в процедуре отобр (рис. 13.8),так что процедуру отобр2 можно получить,внеся в отобр изменения, связанные сдругим представлением деревьев. Другая полезнаямодификация - заменить в отобр цель write(Верш) на процедуру, определяемуюпользователем

печверш( Верш, H)

которая выведет Верш в удобной дляпользователя форме, а также конкретизирует Н в соответствии с количеством символов,необходимом для представления Верш вэтой форме. В дальнейшем Н будетиспользоваться как величина отступа дляподдеревьев.

Резюме

И / ИЛИ-граф - это формальный аппарат для представления задач. Такое представление является наиболее естественным и удобным для задач, которые разбиваются на независимые подзадачи. Примером могут служить игры.

Вершины И / ИЛИ-графа бывают двух типов: И- вершины и ИЛИ-вершины.

Конкретная задача определяется стартовой вершиной и целевым условием. Решение задачи представляется решающим деревом.

Для моделирования оптимизационных задач в И / ИЛИ-граф можно ввести стоимости дуг и вершин.

Процесс решения задачи, представленной И / ИЛИ-графом, включает в себя поиск в графе. Стратегия поиска в глубину предусматривает систематический просмотр графа и легко программируется. Однако эта стратегия может привести к неэффективности из-за комбинаторного взрыва.

Для оценки трудности задач можно применить эвристики, а для управления поиском - принцип эвристического поиска с предпочтением. Эта стратегия более трудна в реализации.

В данной главе были разработаны прологовские программы для поиска в глубину и поиска с предпочтением в И / ИЛИ-графах.

Были введены следующие понятия:

И / ИЛИ-графы

И-дуги, ИЛИ-дуги

И-вершины, ИЛИ-вершины

решающий путь, решающее дерево

стоимость дуг и вершин

эвристические оценки в И / ИЛИ-графах

"возвращенные" оценки

поиск в глубину в И / ИЛИ-графах

поиск с предпочтением в И / ИЛИ-графах

Литература

И / ИЛИ-графы и связанные с ними алгоритмыпоиска являются частью классических механизмовискусственного интеллекта для решения задач иреализации машинных игр. Ранним примеромприкладной задачи, использующей эти методы,может служить программа символическогоинтегрирования (Slagle 1963). И / ИЛИ-поискиспользуется в самой пролог-системе. Общееописание И / ИЛИ-графов и алгоритма можно найти вучебниках по искусственному интеллекту (Nilsson 1971;Nilsson 1980). Наша программа поиска с предпочтением -это один из вариантов алгоритма, известного подназванием АО* . Формальные свойства АО* -алгоритма(включая его допустимость) изучались несколькимиавторами. Подробный обзор полученныхрезультатов можно найти в книге Pearl (1984).

Nilsson N.J. (1971). Problem-Solving Methods in Artificial Intelligence.McGraw-Hill.

Nilsson N.J. (1980). Principles of Artificial Intelligence. Tioga; alsoSpringer-Verlag.

Pearl J. (1984). Heuristics: Intelligent Search Strategies for Computer ProblemSolving. Addison-Wesley.

Slagle J.R. (1963). A heuristic program that solves symbolic integration problems infreshman calculus. In: Computers and Thought (E. Feigenbaum, J. Feldman, eds.).McGraw-Hill.

Назад | Содержание| Вперёд

Оглавление