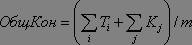Назад | Содержание| Вперёд 12. 3. Применение поиска спредпочтением к планир...

Назад | Содержание| Вперёд

12. 3. Применение поиска спредпочтением к планированиювыполнения задач

Рассмотрим следующую задачу планирования. Данасовокупность задач t₁, t₂, ...,имеющих времена выполнения соответственно T1,Т2, ... . Все эти задачи нужно решить на m идентичных процессорах. Каждая задача можетбыть решена на любом процессоре, но в каждыйданный момент каждый процессор решает толькоодну из задач. Между задачами существуетотношение предшествования, определяющее, какиезадачи (если таковые есть) должны быть завершены,прежде чем данная задача может быть запущена.Необходимо распределить задачи междупроцессорами без нарушения отношенияпредшествования, причем таким образом, чтобы всясовокупность задач была решена за минимальноевремя. Время, когда последняя задача всоответствии с выработанным планом завершаетсвое решение, называется временем окончанияплана. Мы хотим минимизировать время окончанияпо всем возможным планам.

На рис. 12.8 показан пример задачи планирования, атакже приведено два корректных плана, один изкоторых оптимален. Из примера видно, чтооптимальный план обладает одним интереснымсвойством, а именно в нем можетпредусматриваться "время простоя"процессоров. В оптимальном плане рис. 12.8процессор 1, выполнив задачу t, ждет в течение двух квантов времени, несмотря нато, что он мог бы начать выполнение задачи t.

Один из способов построить план можно грубосформулировать так. Начинаем с пустого плана (снезаполненными временными промежутками длякаждого процессора) и постепенно включаем в негозадачи

где m - число процессоров. Пустьвремя окончания текущего частичного плана равно

Кон = maх(K_j).

Тогда эвристическая оценка Н (дополнительное время для включения в частичныйплан ждущих задач) определяется следующимвыражением:

if ОбщКон>Кон then Н = ОбщКон-Кон else H=0

Программа, содержащая определения отношений,связанных с пространством состояний нашейзадачи планирования, приведена полностью на рис.12.9. Эта программа включает в себя такжеспецификацию конкретной задачи планирования,показанной на рис. 12.3. Одно из оптимальныхрешений, полученных в процессе поиска спредпочтением в определенном таким образомпространстве состояний, показано на рис. 12.8.

Проект

Вообще говоря, задачи планированияхарактеризуются значительной комбинаторнойсложностью. Наша простая эвристическая функцияне обеспечивает высокой эффективностиуправления поиском. Предложите другиеэвристические функции и проведите с нимиэксперименты.

/* Отношения для задачи планирования.

Вершины пространства состояний - частичныепланы,

записываемые как

[ Задача1/Т1,Задача2/Т2, ...]*

[ Задача1/К1, Задача2/К2, ...]*ВремяОкончания

В первом списке указываются ждущие задачи ипродолжительности их выполнения; во втором -текущие решаемые задачи и их времена окончания,упорядоченные так, чтобы выполнялисьнеравенства K1<=K2, K2<=K3, ... . Время окончанияплана - самое последнее по времени времяокончания задачи.

после( Задачи1*[ _ /К |Акт1]*Кон1, Задачи2*Акт2*Кон2,Ст):-

удалить( Задача/Т, Задачи1, Задачи2),

% Взять ждущую задачу

not( принадлежит( Здч1/_, Задачи2),

раньше( ЗДЧ, Задача) ),

% Проверить предшествование

not( принадлежит( Здч1/К1, Акт1), К1<К2,

раньше( К1, Задача) ), % Активныезадачи

Время is К + Т,

% Время окончания работающей задачи

встав( ЗадачаВремя, Акт1, Акт2, Кон1, Кон2),

Ст is Кон2 - Кон1.

после( Задачи*[ _ /К |Акт1]*Кон, Задачи2*Акт2*Кон, 0):-

вставпростой( К, Акт1, Акт2).

% Оставить процессор бездействующим

раньше( Задача1,Задача2) :-

% В соответствии с предшествованием

предш( Задача1, Задача2).

% Задача1 раньше, чем Задача2

раньше( Здч1, Здч2) :-

предш( Здч, Здч2),

раньше( Здч1, Здч).

встав( Здч/А, [Здч1/В |Спис], [Здч/А, Здч1/В | Спис], К, К):-

% Список задач упорядочен

А =< В, !.

встав( Здч/А, [Здч1/В |Спнс], [Здч1/В | Спис1], К1, К2) :-

встав( Здч/А, Спис, Спис1, Kl, К2).

встав( Здч/А, [ ],[Здч/А], _, А).

вставпростой( А,[Здч/В | Спис], [простой/В, Здч/В | Спис]):-

% Оставить процессор бездействующим

А < В, ! %До ближайшего времени окончания

вставпростой( А,[Здч/В | Спис], [Здч/В | Спис1]) :-

вставпростой( А, Спис, Спис1 ).

удалить( А, [А | Спис],Спис ).

% Удалить элемент из списка

удалить( А, [В | Спис],[В | Спис1] ):-

удалить( А, Спис, Спис1 ).

цель( [ ] *_*_ ). % Целевоесостояние: нет ждущих задач

% Эвристическая оценка частичного планаоснована на

% оптимистической оценке последнего времениокончания

% этого частичного плана,

% дополненного всеми остальными ждущимизадачами.

h( Задачи *Процессоры * Кон, Н) :-

сумвремя( Задачи, СумВремя),

% Суммарная продолжительность

% ждущих задач

всепроц( Процессоры, КонВремя, N),

% КонВремя - сумма времен окончания

% для процессоров, N - их количество

ОбщКон is ( СумВремя + КонВремя)/N,

( ОбщКон > Кон, !, H is ОбщКон - Кон; Н = 0).

сумвремя( [ ], 0).

сумвремя( [ _ /Т |Задачи], Вр) :-

сумвремя( Задачи, Вр1),

Вр is Bp1 + Т.

всепроц( [ ], 0, 0).

всепроц( [ _ /T |СписПроц], КонВр, N) :-

всепроц( СписПроц, КонВр1, N1),

N is N1 + 1,

КонВр is КонВр1 + Т.

% Граф предшествования задач

предш( t1, t4). предш( t1, t5). предш( t2, t4).

предш( t2, t5). предш( t3, t5). предш( t3, t6).

предш( t3, t7).

% Стартовая вершина

старт( [t1/4, t2/2, t3/2,t4/20, t5/20, t6/11, t7/11] *

[простой/0, простой/0, простой/0] * 0 ).

Рис. 12. 9. Отношения длязадачи планирования. Даны также

определения отношений для конкретной задачипланирования с

рис. 12.8: граф предшествования и исходный(пустой) план в

качестве стартовой вершины.

Резюме

Для оценки степени удаленности некоторой вершины пространства состояний от ближайшей целевой вершины можно использовать эвристическую информацию. В этой главе были рассмотрены численные эвристические оценки.

Эвристический принцип поиска с предпочтением направляет процесс поиска таким образом, что для продолжения поиска всегда выбирается вершина, наиболее перспективная с точки зрения эвристической оценки.

В этой главе был запрограммирован алгоритм поиска, основанный на указанном принципе и известный в литературе как А*-алгоритм.

Для того, чтобы решить конкретную задачу при помощи А*-алгоритма, необходимо определить пространство состояний и эвристическую функцию. Для сложных задач наиболее трудным моментом является подбор хорошей эвристической функции.

Теорема о допустимости помогает установить, всегда ли А*-алгоритм, использующий некоторую конкретную эвристическую функцию, находит оптимальное решение.

Литература

Программа поиска с предпочтением,представленная в настоящей главе, - это один измногих вариантов похожих друг на друга программ,из которых А*-алгоритм наиболее популярен. Общееописание А*-алгоритма можно найти в книгах Nillson(1971, 1980) или Winston (1984). Теорема о допустимостивпервые доказана авторами статьи Hart, Nilsson, and Raphael(1968). Превосходное и строгое изложение многихразновидностей алгоритмов поиска спредпочтением и связанных с ними математическихрезультатов дано в книге Pearl (1984). В статье Doran andMichie (1966) впервые изложен поиск с предпочтением,управляемый оценкой расстояния до цели.

Головоломка "игра в восемь"использовалась многими исследователями вобласти искусственного интеллекта в качестветестовой задачи при изучении эвристическихпринципов (см., например, Doran and Michie (1966), Michie and Ross(1970) и Gaschnig (1979) ).

Задача планирования, рассмотренная в настоящейглаве, также как и многие ее разновидности,возникает во многих прикладных областях вситуации, когда необходимо спланироватьобслуживание запросов на ресурсы. Один изпримеров - операционные системы вычислительныхмашин. Задача планирования со ссылкой на этоконкретное приложение изложена в книге Coffman andDenning (1973).

Найти хорошую эвристику - дело важное и трудное,поэтому изучение эвристик - одна из центральныхтем в искусственном интеллекте. Существуют,однако, некоторые границы, за которые невозможновыйти, двигаясь в направлении улучшения качестваэвристик. Казалось бы, все, что необходимо дляэффективного решения комбинаторной задачи - этонайти мощную эвристику. Однако есть задачи (в томчисле многие задачи планирования), для которых несуществует универсальной эвристики,обеспечивающей во всех случаях какэффективность, так и допустимость. Многиетеоретические результаты, имеющие отношение кэтому ограничению, собраны в работе Garey and Johnson(1979).

Coffman E.G. and Denning P.J. (1973). Operating Systems Theory. Prentice-Hall.

Doran J. and Michie D. (1966). Experiments with the graph traverser program. Proc.Royal Socieiy of London 294(A): 235-259.

Garey M. R. and Johnson D. S. (1979). Computers and Intractability. W. H.Freeman. [Имеется перевод: Гэри M., Джонсон Д. С-Вычислительные машины и труднорешаемые задачи.-M.: Мир, 1982.]

Gaschnig J. (1979). Performance measurement and analysis of certain search algorithms.Carnegie-Mellon University: Computer Science Department-Technical Report CMU-CS-79-124(Ph. D. Thesis).

Hart P.E., Nilsson N.J. and Raphael B. (1968). A formal basis for the heuristicdetermination of minimum cost paths. IEEE Transactions on Systems Sciences andCybernetics SSC-4(2):100-107

Michie D. and Ross R. (1970). Experiments with the adaptive graph traverser. MachineIntelligence 5: 301-308.

Nilsson N.J. (1971). Problem - Solving Methods in Artificial Intelligence.McGraw-Hill. [Имеется перевод: Нильсон H. Искусственныйинтеллект. Методы поиска решений. - M: Мир, 1973.]

Nilsson N. J. (1980). Principles of Artificial Intelligence. Tioga; alsoSpringer-Verlag.

Pearl J. (1984). Heuristics: Intelligent Search Strategies for Computer ProblemSolving. Addison-Wesley.

Winston P. H. (1984). Artificial Intelligence (second edition).Addison-Wesley. [Имеется перевод первого издания:Уинстон П. Искусственный интеллект. - M.: Мир, 1980.]

Назад | Содержание| Вперёд

Оглавление