Назад | Содержание| Вперёд Глава 12 ПОИСК С ПРЕДПОЧ...

Назад | Содержание| Вперёд

Глава 12

ПОИСК С ПРЕДПОЧТЕНИЕМ: ЭВРИСТИЧЕСКИЙПОИСК

Поиск в графах при решении задач, как правило,невозможен без решения проблемы комбинаторнойсложности, возникающей из-за быстрого роста числа альтернатив. Эффективным средствомборьбы с этим служит эвристическийпоиск.

Один из путей использованияэвристической информации о задаче - этополучение численных эвристическихоценок для вершин пространства состояний.Оценка вершины указывает нам, насколько даннаявершина перспективна с точки зрения достиженияцели. Идея состоит в том, чтобы всегда продолжатьпоиск, начиная с наиболее перспективной вершины,выбранной из всего множества кандидатов. Именнона этом принципе основана программа поиска спредпочтением, описанная в данной главе.

12. 1. Поиск с предпочтением

Программу поиска с предпочтением можнополучить как результат усовершенствованияпрограммы поиска в ширину (рис. 11.13). Подобнопоиску в ширину, поиск с предпочтениемначинается со стартовой вершины и используетмножество путей-кандидатов. В то время, как поискв ширину всегда выбирает для продолжения самыйкороткий путь (т.е. переходит в вершинынаименьшей глубины), поиск с предпочтениемвносит в этот принцип следующееусовершенствование: для каждого кандидатавычисляется оценка и для продолжения выбираетсякандидат с наилучшей оценкой.

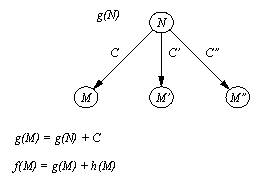
Рис. 12. 5. Связь между g-оценкойвершины В и f- и g-оценками

ее "детей" в пространстве состояний.

Алгоритм поиска пути называют допустимым,если он всегда отыскивает оптимальное решение(т.е. путь минимальной стоимости) при условии, чтотакой путь существует. Наша реализация алгоритмапоиска, пользуясь механизмом возвратов, выдаетвсе существующие решения, поэтому, в нашемслучае, условием допустимости следует считатьоптимальность первого из найденных решений.Обозначим через h*(n) стоимостьоптимального пути из произвольной вершины n в целевую вершину. Верна следующая теорема одопустимости А*-алгоритма: А*-алгоритм,использующий эвристическую функцию h, является допустимым, если

h( n) <= h*( n)

для всех вершин n пространствасостояний.

Этот результат имеет огромное практическоезначение. Даже если нам не известно точноезначение h*, нам достаточно найтикакую-либо нижнюю грань h* ииспользовать ее в качестве h вА*-алгоритме - оптимальность решения будетгарантирована.

Существует тривиальная нижняя грань, а именно:

h( n) = 0, для всех вершин n пространствасостояний.

И при таком значении h допустимостьгарантирована. Однако такая оценка не имеетникакой эвристической силы и ничем не помогаетпоиску. А*-алгоритм при h=0 ведет себяаналогично поиску в ширину. Он, действительно,превращается в поиск в ширину, если, кроме того,положить с(n, n' )=1 для всех дуг (n,n') пространства состояний. Отсутствиеэвристической силы оценки приводит к большойкомбинаторной сложности алгоритма. Поэтомухотелось бы иметь такую оценку h, которая была бы нижней гранью h* (чтобы обеспечить допустимость) и, кроме того,была бы как можно ближе к h* (чтобыобеспечить эффективность). В идеальном случае,если бы нам была известна сама точная оценка h*, мы бы ее и использовали: А*-алгоритм,пользующийся h*, находитоптимальное решение сразу, без единого возврата.

Упражнение

12. 1. Определите отношения после,цель и h для задачипоиска маршрута рис. 12.2. Посмотрите, как нашалгоритм поиска с предпочтением будет вести себяпри решении этой задачи.

Назад | Содержание| Вперёд

Оглавление