Назад | Содержание| Вперёд 11. 3. Поиск в ширину В противоположно...

Назад | Содержание| Вперёд

11. 3. Поиск в ширину

В противоположность поиску в глубину стратегияпоиска в ширину предусматривает переход в первуюочередь к вершинам, ближайший к стартовойвершине. В результате процесс поиска имееттенденцию развиваться более в ширину, чем вглубину, что иллюстрирует рис. 11.9.

Поиск в ширину программируется не так легко,как поиск в глубину. Причина состоят в том, что

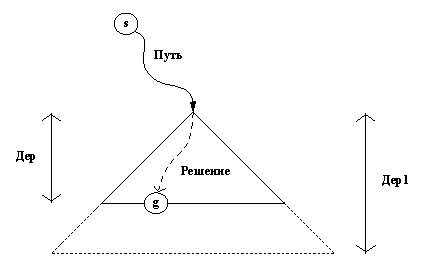
Рис. 11. 12. Отношение paсширить(Путь, Дер, Дер1, ЕстьРеш, Решение):

s - стартовая вершина, g- целевая вершина. Решение - это Путь,

продолженный вплоть до g. Дер1- результат расширения дерева

Дер на один уровень вниз.

получить поддерево Дер1 как результатрасширения Дер на один уровень. Но вслучае, когда в процессе расширения поддерева Дервстретится целевая вершина, процедура расширитьдолжна сформировать соответствующий решающийпуть.

Итак, процедура расширить будетпорождать два типа результатов. На конкретныйвид результата будет указывать значениепеременной ЕстьРеш:

(1) ЕстьРеш = да

Решение= решающий путь, т. е. Путь, продолженныйдо целевой вершины.

Дер1= неконкретизировано.

Разумеется, такой тип результата получитсятолько в том случае, когда Дер будетсодержать целевую вершину. Добавим также, что этацелевая вершина обязана быть листом поддерева Дер.

(2) ЕстьРеш = нет

Дер1= результат расширения поддерева Дер наодин уровень вниз от своего "подножья". Дер1не содержит ни одной "тупиковой" ветви из Дер,т. е. такой ветви, что она либо не может бытьпродолжена из-за отсутствия преемников, либолюбое ее продолжение приводит к циклу.

Решение= неконкретизировано.

Если в дереве Дер нет ни одной целевойвершины и, кроме того, оно не может бытьрасширено, то процедура расширитьтерпит неудачу.

Процедура верхнего уровня для поиска в ширину

вширину( Дер,Решение)

отыскивает Решение либо средимножества кандидатов Дер, либо в егорасширении. На рис. 11.3 показано, как выглядитпрограмма целиком. В этой программе имеетсявспомогательная процедура расширитьвсе.Она расширяет все деревья из некоторого списка,и затем, выбросив все "тупиковые"деревья", собирает все полученные расширенныедеревья в один новый список. Используя механизмвозвратов, она также порождает все решения,обнаруженные в деревьях из списка. Имеется однадополнительная деталь: по крайней мере одно издеревьев должно "вырасти". Если это не так,то процедуре расширитьвсе не удаетсяполучить ни одного расширенного дерева - вседеревья из списка оказываются "тупиковыми".

% ПОИСК В ШИРИНУ

% Множество кандидатов представлено деревом

решить( Старт,Решение) :-

вширину( л( Старт), Решение).

вширину( Дер,Решение) :-

расширить( [ ], Дер, Дер1, ЕстьРеш, Решение),

( ЕстьРеш = да;

ЕстьРеш = нет, вширину( Дер1, Решение) ).

расширить( П, Л( В), _,да, [В | П] ) :-

цель( В).

расширить( П, Л( В), д(В, Пд), нет, _ ) :-

bagof( л( B1),

( после( В, B1), not принадлежит( В1, П)), Пд).

расширить( П, д( В,Пд), д( В, Пд1), ЕстьРеш, Реш) :-

расширитьвсе( [В | П], Пд, [ ], Пд1, ЕстьРеш, Реш).

расширитьвсе( _, [ ],[Д | ДД], [Д | ДД], нет, _ ).

% По крайней мере одно дерево должно вырасти

расширитьвсе( П, [Д |ДД], ДД1, Пд1, ЕстьРеш, Реш) :-

расширить ( П, Д, Д1, ЕстьРеш1, Реш),

( ЕстьРеш 1= да, ЕстьРеш = да;

ЕстьРеш1 = нет, !,

расширитьвсе( П, ДД, [Д1 | ДД1], Пд1, ЕстьРеш, Реш));

расширитьвсе( П, ДД, ДД1, Пд1, ЕстьРеш, Реш ).

Рис. 11. 13. Реализацияпоиска в ширину с использованием

древовидного представления множествапутей-кандидатов.

Мы разработали эту более сложную реализациюпоиска в ширину не только для того, чтобыполучать программу более экономичную посравнению с предыдущей версией, но также ипотому, что такое решение задачи может послужитьхорошим стартом для перехода к усложненнымпрограммам поиска, управляемым эвристиками,таким как программа поиска с предпочтением из гл.12.

Упражнения

11. 5. Перепишите программупоиска в ширину рис. 11.10, используя разностноепредставление для списка путей-кандидатов ипокажите, что в результате получится программа,приведенная на рис. 11.11. Зачем в программу рис. 11.11включена цель

Пути \== Z

Проверьте, что случится при поиске впространстве состояний рис. 11.9, если эту цельопустить. Различие в выполнении программы,возникнет только при попытке найти новые решенияв ситуации, когда не осталось больше ни одногорешения.

11. 6. Как программынастоящего раздела можно использовать дляпоиска, начинающегося от стартового множествавершин, вместо одной стартовой вершины?

Посмотреть ответ

11. 7. Как программы этой главыможно использовать для поиска в обратномнаправлении, т.е. от целевой вершины к стартовойвершине (или к одной из стартовых вершин, если ихнесколько). Указание: переопределите отношение после.В каких ситуациях обратный поиск будет иметьпреимущества перед прямым поиском?

11. 8. Иногда выгодносделать поиск двунаправленным, т. е.продвигаться одновременно с двух сторон отстартовой и целевой вершин. Поиск заканчивается,когда оба пути "встречаются". Определитепространство поиска (отношение после) ицелевое отношение для заданного графа такимобразом, чтобы наши процедуры поиска вдействительности выполняли двунаправленныйпоиск.

11. 9. Проведите экспериментыс различными методами поиска применительно кзадаче планирования в "мире кубиков".

Назад | Содержание| Вперёд

Оглавление