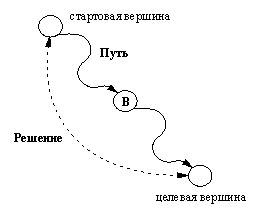
Назад | Содержание| Вперёд 11. 2. Стратегия поиска вглубину Сущес...

Назад | Содержание| Вперёд

11. 2. Стратегия поиска вглубину

Существует много различных подходов к проблемепоиска решающего пути для задач,сформулированных в терминах пространствасостояний. Основные две стратегии поиска - этопоиск в глубину и поиск в ширину. Внастоящем разделе мы реализуем первую из них.

Мы начнем разработку алгоритма и его вариантовсо следующей простой идеи:

Для того, чтобы найти решающий путь Решиз заданной вершины В в некоторуюцелевую вершину, необходимо:

если В - это целевая вершина, то положить Реш = [В], или

если для исходной вершины В существует вершина-преемник В1, такая, что можно провести путь Реш1 из В1 в целевую вершину, то положить Реш = [В | Peш1].

Рис. 11. 6. Отношение вглубину(Путь, В, Решение).

Для облегчения программирования вершины всписках, представляющих пути, будутрасставляться в обратном порядке. Аргумент Путьнужен для того,

(1) чтобы нерассматривать тех преемников вершины Верш,которые уже встречались раньше (обнаружениециклов);

(2) чтобы облегчитьпостроение решающего пути Решение.Соответствующая программа поиска в глубинупоказана на рис. 11.7.

решить( Верш,Решение) :-

вглубину( [ ], Верш, Решение).

вглубину( Путь,Верш, [Верш | Путь] ) :-

цель( Верш).

вглубину( Путь,Верш, Реш) :-

после( Верш, Верш1),

not принадлежит( Верш1, Путь), % Цикл ?

вглубину( [Верш | Путь], Верш1, Реш).

Рис. 11. 7. Программапоиска в глубину без зацикливания.

Теперь наметим один вариант этой программы.Аргументы Путь и Вершпроцедуры вглубину можно объединить водин список [Верш | Путь]. Тогда, вместовершины-кандидата Верш, претендующей нато, что она находится на пути, ведущем к цели, мыбудем иметь путь-кандидат П = [Верш |Путь], который претендует на то, что егоможно продолжить вплоть до целевой вершины.Программирование соответствующего предиката

вглубину( П,Решение)

оставим читателю в качестве упражнения.

Наша процедура поиска в глубину, снабженнаямеханизмом обнаружения циклов, будет успешнонаходить решающие пути в пространствахсостояний, подобных показанному на рис. 11.5.Существуют, однако, такие пространствасостоянии, в которых наша процедура не дойдет доцели. Дело в том, что многие пространствасостояний бесконечны. В таком пространствеалгоритм поиска в глубину может "потерять"цель, двигаясь вдоль бесконечной ветви графа.Программа будет бесконечно долго обследоватьэту бесконечную область пространства, так и неприблизившись к цели. Пространство состоянийзадачи о восьми ферзях, определенное так, как этосделано в настоящем разделе, на первый взглядсодержит ловушку именно такого рода. Нооказывается, что оно все-таки конечно, посколькуY-координаты выбираются из ограниченногомножества, и поэтому на доску можно поставить"безопасным образом" не более восьми ферзей.

вглубину2( Верш,[Верш], _ ) :-

цель( Верш).

вглубину2( Верш,[Верш | Реш], МаксГлуб) :-

МаксГлуб > 0,

после( Верш, Верш1),

Maкс1 is МаксГлуб - 1,

вглубину2( Верш1, Реш, Maкс1).

Рис. 11. 8. Программапоиска в глубину с ограничением по глубине.

Для того, чтобы предотвратить бесцельноеблуждание по бесконечным ветвям, мы можемдобавить

в базовую процедуру поиска вглубину еще одно усовершенствование, а именно,ввести

ограничение на глубину поиска

.Процедура поиска в глубину будет тогда иметьследующие аргументы:

вглубину2( Верш,Решение, МаксГлуб)

Не разрешается вести поиск на глубине большей,чем МаксГлуб. Программная реализацияэтого ограничения сводится к уменьшению наединицу величины предела глубины при каждомрекурсивном обращений к вглубину2 и кпроверке, что этот предел не стал отрицательным.В результате получаем программу, показанную нарис. 11.8.

Упражнения

11. 1. Напишите процедурупоиска в глубину (с обнаружением циклов)

вглубину1(ПутьКандидат, Решение)

отыскивающую решающий путь Решениекак продолжение пути ПутьКандидат. Обапути представляйте списками вершин,расположенных в обратном порядке так, чтоцелевая вершина окажется в голове списка Решение.

Посмотреть ответ

11. 2. Напишите процедурупоиска в глубину, сочетающую в себе обнаружениециклов с ограничением глубины, используя рис. 11.7и 11.8.

11. 3. Проведите экспериментпо применению программы поиска в глубину кзадаче планирования в "мире кубиков" (рис.11.1).

11. 4. Напишите процедуру

отобр( Ситуация)

для отображения состояния задачи"перестановки кубиков". Пусть Ситуация- это список столбиков, а столбик, в свою очередь, -список кубиков. Цель

отобр( [ [a], [e, d], [с, b] ])

должна отпечатать соответствующую ситуацию,например так:

е с

a d b

================

Назад | Содержание| Вперёд

Оглавление