Назад | Содержание| Вперёд 10. 2. AVL - дерево: приближенносбалансированное...

Назад | Содержание| Вперёд

10. 2.    AVL - дерево: приближенносбалансированное дерево

AVL-дерево - это дерево, обладающееследующими свойствами:

(1)        Левое и правоеподдеревья отличаются по глубине не более чем на1.

(2)        Оба поддереваявляются AVL-деревьями.

Деревья, удовлетворяющие этому определению,могут быть слегка разбалансированными. Однакоможно показать, что даже в худшем случае глубинаAVL-дерева примерно пропорциональна log n, где n- число вершин дерева. Таким образомгарантируется логарифмический порядокпроизводительности операций внутри, добавитьи удалить.

Операции над AVL-деревом работают посуществу так же, как и над двоичным справочником.В них только сделаны добавления, связанные споддержанием приближенной сбалансированностидерева. Если после вставления или удалениядерево перестает быть приближенносбалансированным, то специальные механизмывозвращают ему требуемую степеньсбалансированности. Для того, чтобы эффективнореализовать этот механизм, нам придетсясохранять некоторую дополнительную информациюотносительно степени сбалансированности дерева.На самом деле, нам нужно знать только разностьмежду глубинами поддеревьев, которая можетпринимать значения -1, 0 или +1. Тем не менее дляпростоты мы предпочтем сохранять сами величины глубин поддеревьев, а не разности междуними.

Мы определим отношение вставленияэлемента как

        доб_avl( Дер, X, НовДер)

где оба дерева Дер и НовДер -это AVL-деревья, причем НовДер полученоиз Дер вставлением элемента X.AVL-деревья будем представлять как термы вида

        д( Лев, А, Прав)/Глуб

где А - корень, Лев и Прав- поддеревья, а Глуб -

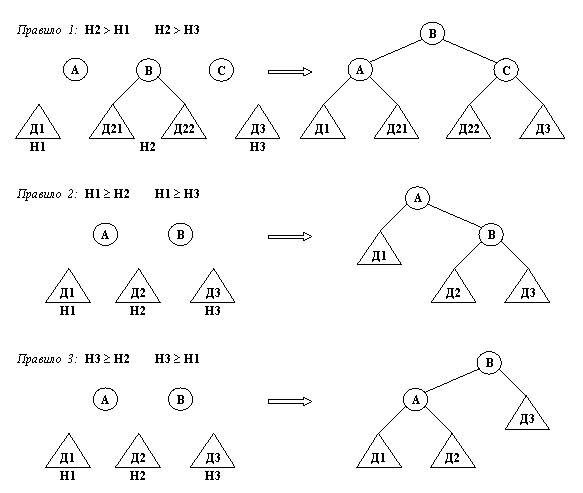
Рис. 10. 9.  Три правилапостроения нового AVL-дepевa.

глубину h +1.

В случае, когда Х меньше, чем А, имееманалогичную ситуацию, причем левое и правоеподдеревья меняются местами. Таким образом, влюбом случае мы должны построить дерево НовДер,используя три дерева (назовем их Дер1, Дер2и Дер3) и два отдельных элемента А и В.Теперь рассмотрим вопрос: как соединить междусобой эти пять составных частей, чтобы дерево НовДербыло AVL-справочником? Ясно, что они должнырасполагаться внутри НовДер вследующем порядке (слева направо):

        Дер1, А, Дер2, В, Дер3

Рассмотрим три случая:

(1)        Среднее дерево Дер2глубже остальных двух деревьев.

(2)        Дер1 имеетглубину не меньше, чем Дер2 и Дер3.

(3)        Дер3 имеетглубину не меньше, чем Дер2 и Дер1.

На рис. 10.9 видно, как можно построить дерево НовДерв каждом из этих трех случаев. Например, в случае 1среднее дерево Дер2 следует разбить надва части, а затем включить их в состав НовДер.Три правила, показанные на pис.10.9, нетруднозапасать на Прологе в виде отношения

        соединить( Дер, А,Дер2, В, Дер3, НовДер)

Последний аргумент НовДер - этоAVL-дерево, построенное из пяти составных частей,пяти первых аргументов. Правило 1, например,принимает вид:

        соединить( Д1/Н1, А, д(Д21, В, Д22)/Н2, С, Д3/Н3,