Назад | Содержание| Вперёд Глава 10 УСОВЕРШЕНСТВОВА...

Назад | Содержание| Вперёд

Глава 10

УСОВЕРШЕНСТВОВАННЫЕ МЕТОДЫ

ПРЕДСТАВЛЕНИЯ МНОЖЕСТВ ДЕРЕВЬЯМИ

В данной главе мы рассмотримусовершенствованные методы представлениямножеств при помощи деревьев. Основная идеясостоит в том, чтобы поддерживатьсбалансированности или приближеннуюсбалансированность дерева, с тем чтобы избежатьвырождения его в список. Механизмы балансировкидеревьев гарантируют, даже в худшем случае,относительно быстрый доступ к элементам данных,хранящихся в дереве, при логарифмическом порядкевремени доступа. В этой главе изложено два такихмеханизма: двоично-троичные (кратко, 2-3) деревья иAVL-деревья. (Для изучения остальных главпонимание данной главы не обязательно.)

10. 1. Двоично - троичные справочники

Двоичное дерево называют хорошосбалансированным, если оба его поддерева имеютпримерно одинаковую глубину (или размер) и самисбалансированы. Глубина сбалансированногодерева приближенно равна log n , где n -число вершин дерева. Время, необходимое длявычислений, производимых отношениями внутри,добавить и удалить наддвоичными справочниками, пропорциональноглубине дерева. Таким образом, в случае двоичныхсправочников это время имеет порядок log n.Логарифмический рост сложности алгоритма,проверяющего принадлежность элемента множеству,- это определенное достижение по сравнению сосписковым представлением, поскольку в последнемслучае мы имеем линейный рост сложности

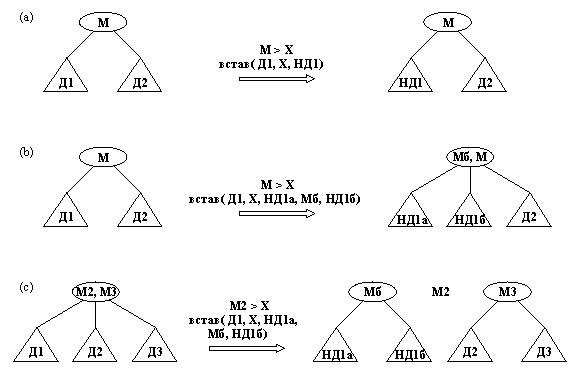
Рис. 10. 5. Некоторые из случаев работы отношения встав.

(a) встав( в2( Д1, М, Д2), X, в2( НД1, М, Д2) );

(b) встав( в2( Д1, М, Д2), X,

в3( НД1а, Мб, НД1б, М, Д2) );

в2( НД1а, Мб, НД1б), М2, в2( Д2, М3, Д3) ).

% Вставление элемента в 2-3 справочник

доб23( Дер, X, Дер1) :- %Вставить Х в Дер, получить Дер1

встав( Дер, X, Дер1). % Дерево растет вширь

доб23( Дер, X, в2( Д1, М2,Д2) ) :-

встав( Дер, X, Д1, М2, Д2). %Дерево растет вглубь

доб23( nil, X, л( Х) ).

встав( л( А), X, л( А), X,л( Х) ) :-

больше( X, А).

встав( л( А), X, л( Х), А,л( А) ) :-

больше( А, X).

встав( в2( Д1, М, Д2), X,в2( НД1, М, Д2) ) :-

больше( М, X),

встав( Д1, X, НД1).

встав( в2( Д1, М, Д2), Х,в3( НД1а, Мб, НД1б, М, Д2) ) :-

больше( М, X),

встав( Д1, X, НД1а, Мб, НД1б).

встав( в2( Д1, М, Д2), X,в2( Д1, М, НД2) ) :-

больше( X, М),

встав( Д2, X, НД2).

встав( в2( Д1, М, Д2), Х,в3( Д1, М, НД2а, Мб, НД2б) ) :-

больше( X, М),

встав( Д2, X, НД2а, Мб, НД2б).

встав( в3( Д1, М2, Д2, М3,Д3), Х, в3( НД1, М2, Д2, М3, Д3) :-

больше( М2, X),

встав( Д1, X, НД1).