Назад | Содержание| Вперёд 9. 3. Двоичные справочники: добавлениеи удаление...

Назад | Содержание| Вперёд

9. 3. Двоичные справочники: добавлениеи удаление элемента

Если мы имеем дело с динамически изменяемыммножеством элементов данных, то нам можетпонадобиться внести в него новый элемент илиудалить из него один из старых. В связи с этимнабор основных операций, выполняемых надмножеством S, таков:

внутри( X, S) %Х содержится в S

добавить( S, X, S1) %Добавить Х к S, результат - S1

удалить( S, X, S1) %Удалить Х из S, результат - S1

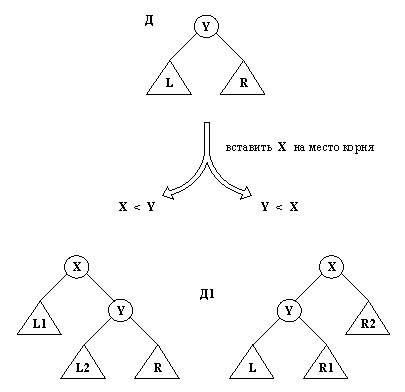
Рис. 9. 14. Внесение Х вдвоичный справочник в качестве корня.

Ответ мы получим, если учтем следующиеограничения на L1, L2:

L1 и L2 - двоичные справочники;

множество всех вершин, содержащихся как в L1, так и в L2, совпадает с множеством вершин справочника L;

все вершины из L1 меньше, чем X; все вершены из L2 больше, чем X.

Отношение, которое способно наложить все этиограничения на L1, L2, - это как раз и есть нашеотношение добкор. Действительно, еслибы мы вводили Х в L на место корня, то поддеревьямирезультирующего дерева как раз и оказались бы L1 иL2. В терминах Пролога L1 и L2 должны быть такими,чтобы достигалась цель

добкор( L, X, дер( L1, X,L2) ).

Те же самые ограничения применимы к R1, R2:

добкор( R, X, дер( R1, X,R2) ).

добавить( Д, X, Д1) :- % Добавить Х на место корня

добкор( Д, X, Д1).

добавить( дер( L, Y, R),X, дер( L1, Y, R) ) :-

больше( Y, X), % Ввести Х в левое поддерево

добавить( L, X, L1).

добавить( дер( L, Y, R),X, дер( L, Y, R1) ) :-

больше( X, Y), % Ввести Х в правое поддерево

добавить( R, X, R1).

добкор( nil, X, дер( nil,X, nil) ). %Ввести Х в пустое дерево

добкор( дер( L, Y, R), Х,дер( L1, Х, дер( L2, Y, R) )) :-

больше( Y, X),

добкор( L, X, дер( L1, X, L2) ).

добкор( дep( L, Y, R), X,дep( дep( L, Y, R1), X, R2) ) :-

больше( X, Y),

добкор( R, X, дер( R1, X, R2) ).

Рис. 9. 15. Внесениеэлемента на произвольный уровень двоичногосправочника.

На рис. 9.15 показана программа для"недетерминированного" добавления элементав двоичный справочник.

Эта процедура обладает тем замечательнымсвойством, что в нее не заложено никакихограничений на уровень дерева, в которыйвносится новый элемент. В связи с этим операцию добавитьможно использовать "в обратном направлении"для удаления элемента из справочника. Например,приведенная ниже последовательность целейстроит справочник Д, содержащий элементы 3, 5, 1, 6, азатем удаляет из него элемент 5, после чегополучается справочник ДД:

добавить( nil, 3, Д1), добавить( Д1, 5, Д2),

добавить( Д2, 1, Д3), добавить( Д3, 6, Д),

добавить( ДД, 5, Д).

Назад | Содержание| Вперёд

Оглавление