Назад | Содержание| Вперёд 9. 2. Представление множеств двоичнымидеревьями...

               принадлежит( X, L).

Для того, чтобы найти Х в списке L, эта процедурапоследовательно просматривает список элемент заэлементом, пока ей не встретится либо элемент X,либо конец списка. Для длинных списков такойспособ крайне неэффективен.

Для облегчения более эффективной реализацияотношения принадлежности применяют различныедревовидные структуры. В настоящем разделе мырассмотрим двоичные деревья.

Двоичное дерево либо пусто, либосостоит из следующих трех частей:

корень

левое поддерево

правое поддерево

Корень может быть чем угодно, а поддеревьядолжны сами быть двоичными деревьями. На рис. 9.4показано представление множества [а, b, с, d]двоичным деревом. Элементы множества хранятся ввиде вершин дерева. Пустые поддеревья на рис. 9.4не показаны. Например, вершина b имеет дваподдерева, которые оба пусты.

Существует много способов представлениядвоичных деревьев на Прологе. Одна из простыхвозможностей - сделать корень главным функторомсоответствующего терма, а поддеревья - егоаргументами. Тогда дерево рис. 9.4 примет вид

        а( b, с( d) )

Такое представление имеет среди прочих своихнедостатков то слабое место, что для каждойвершины дерева нужен свой функтор. Это можетпривести к неприятностям, если вершины самиявляются структурными объектами.

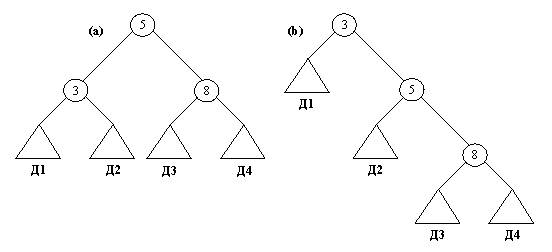
Рис. 9. 8.  (а)    Дерево Д, построенное как результатдостижения целей: внутри( 5, Д), внутри(3, Д), внутри( 8, Д).    (b)    Дерево, полученное при другомпорядке целей: внутри( 5, Д), внутри( 3,Д), внутри( 8, Д).

Здесь уместно сделать несколько замечанийотносительно эффективности поиска всправочниках. Вообще говоря, поиск элемента всправочнике эффективнее, чем поиск в списке. Нонасколько? Пусть n - число элементовмножества. Если множество представлено списком,то ожидаемое время поиска будет пропорциональноего длине n. В среднем нам придетсяпросмотреть примерно половину списка. Еслимножество представлено двоичным деревом, товремя поиска будет пропорционально глубинедерева. Глубина дерева - это длина самогодлинного пути между корнем и листом дерева.Однако следует помнить, что глубина деревазависит от его формы

.

Мы говорим, что дерево (приближенно)сбалансировано, если для каждой вершиныдерева соответствующие два поддерева содержатпримерно равное число элементов. Если деревохорошо сбалансировано, то его глубинапропорциональна log n. В этом случае мыговорим, что дерево имеет логарифмическуюсложность. Сбалансированный справочник лучшесписка настолько же, насколько log n меньше n.К сожалению, это верно только для приближенносбалансированного дерева. Если происходитразбалансировка дерева, то производительностьпадает. В случае полностью разбалансированныхдеревьев, дерево фактически превращается всписок. Глубина дерева в этом случае равна n,а производительность поиска оказывается стольже низкой, как и в случае списка. В связи с этим мывсегда заинтересованы в том, чтобы справочникибыли сбалансированы. Методы достижения этой целимы обсудим в гл. 10.

Упражнения

9. 9.    Определите предикаты

        двдерево( Объект)