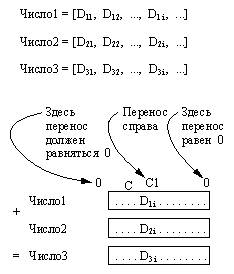
Назад | Содержание| Вперёд Глава 7 ДРУГИЕ ВСТРОЕННЫ...

Назад | Содержание| Вперёд

Глава 7

ДРУГИЕ ВСТРОЕННЫЕ ПРОЦЕДУРЫ

В данной главе мы изучим некоторые другие, неупоминавшиеся ранее встроенные процедуры,предназначенные для более серьезногопрограммирования на Прологе. Эта новые процедурыдают возможность запрограммировать операции,которые известными нам средствамизапрограммировать невозможно. Один набор такихпроцедур касается обработки термов: этипроцедуры проверяют, была ли некотораяпеременная конкретизирована целым числом, ониразбирают термы на части, конструируют новыетермы и т.д. Другой полезный набор процедурработает с "базой данных": процедуры изэтого набора добавляют новые отношения впрограмму или удаляют из нее существующие.

Множество встроенных процедур сильно зависитот конкретной реализации Пролога. Однакопроцедуры, обсуждаемые в данной главе, имеются вомногих реализациях. Различные реализации могутиметь свои наборы дополнительных средств.

7. 1. Проверка типов термов

7. 1. 1. Предикаты var, nоnvar, atom, integer, atomic

Термы бывают разных типов: переменные, целыечисла, атомы и т.д. Если терм - переменная, то внекоторый момент выполнения программы он можетоказаться конкретизированным или неконкретизированным. Далее, если онконкретизирован, то его значение может бытьатомом, структурой и т. п. Иногда бывает полезноузнать, каков тип этого значения. Например, пустьмы хотим сложить значения двух переменных Х и Y:

Z is X + Y

Перед вычислением этой цели необходимо, чтобы Хи Y были конкретизированы целыми числами. Если унас нет уверенности в том, что Х и Y действительноконкретизированы целыми числами, то передвыполнением арифметического действия нужнопроверить это программно.

Для этого следует воспользоваться встроеннымпредикатом integer (целое).Предикат integer( X) принимает значениеистина, если Х - целое или если Х - переменная,имеющая целое значение. Будем говорить в этомслучае, что Х "обозначает" целое. Цель длясложения Х и Y можно тогда "защитить" такойпроверкой переменных Х и Y:

. . ., integer( X), integer( Y), Zis X + Y, . . .

Если неверно, что X и Y оба являются целыми, тосистема и не будет пытаться их сложить. Такимобразом, цели integer "охраняют" цель Zis Х + Y от бессмысленного вычисления.

Встроенные предикаты этого типа таковы: var(переменная), nonvar (непеременная), atom(атом), integer (целое), atomic(атомарный). Они имеют следующий смысл:

var( X)

Эта цель успешна, если Х в текущий момент - неконкретизированная переменная.

nonvar( X)

Эта цель успешна, если Х - терм, отличный отпеременной, или если Х - уже конкретизированная переменная.

atom( X)

Эта цель истинна, если Х обозначает атом.

integer( X)

Цель истинна, если Х обозначает целое.

atomic( X)

Цель истинна, если Х обозначает целое или атом.

Следующие примеры вопросов к пролог-системеиллюстрируют применение этих встроенныхпредикатов:

?- var( Z), Z = 2.

Z = 2

?- Z = 2, var( Z).

?- integer( Z), Z = 2.

?- Z = 2, integer( Z), nonvar(Z).

Z = 2

?- atom( 22).

?- atomic( 22).

yes

?- atom( ==>).

yes

?- atom( p( 1) ).

Необходимость в предикате atomпродемонстрируем на следующем примере. Пусть мыхотим подсчитать, сколько раз заданный атомвстречается в некоторой списке объектов. Дляэтого мы определим процедуру

счетчик( А, L, N)

где А - атом, L - список и N- количество вхождений этого атома. В качествепервой попытки можно было бы определить счетчиктак:

счетчик( _, [ ], 0).

счетчик( A, [A | L], N):- !,

счетчик( A, L, N1),

% N1 - число вхождений атома в хвост

N is N1 + 1.

счетчик( А, [ _ | L], N) :-

счетчик( A, L, N).

Теперь на нескольких примерах посмотрим, какэта процедура работает:

?- счетчик( а, [а, b,а, а], N).

N = 3

?- счетчик( a, [a, b,X, Y], Na).

Na = 3

. . .

?- счетчик( b, [a, b,X, Y], Nb).

Nb = 3

. . .

?- L=[a, b, Х, Y],счетчик( а, L, Na), счетчик( b, L, Nb).

Na = 3

Nb = 1

X = a

Y = a

. . .

В последнем примере как X, так и Y послеконкретизации получили значение а, ипоэтому Nb оказалось равным только 1, однако мыхотели не этого. Нас интересовало количествореальных появлений конкретного атома, авовсе не число термов, сопоставимых с этиматомом. В соответствии с этим более точнымопределением отношения счетчик мыдолжны теперь проверять, является ли головасписка атомом. Усовершенствованная программавыглядит так:

счетчик( _, [ ], 0).

счетчик( А, [В | L], N) :-

atom( В), А = В, !, % B равно атому А?

счетчик( A, L, N1), % Подсчет в хвосте

N is N1 + 1;

счетчик( А, L, N).

% Иначе - подсчитать только в хвосте

В следующем более сложном упражнении попрограммированию числовых ребусов используется предикат nonvar.

7. 1. 2. Решение числовогоребуса с использованием nonvar

Известным примером числового ребуса является

D O N A L D

G E R A L D

R O B E R T

Задача состоит в том. чтобы заменить буквы D, О, Nи т.д. на цифры таким образом, чтобывышеприведенная сумма была правильной. Разнымбуквам должны соответствовать разные цифры,иначе возможно тривиальное решение, например,все буквы можно заменить на нули.

Определим отношение

сумма( Nl, N2, N)

где Nl, N2 и N представляют три числа данногоребуса. Цель cyммa(Nl, N2, N) достигается,если существует такая замена букв цифрами, чтоN1+N2 = N.

Первым шагом к решению будет выборпредставления чисел Nl, N2 и N в программе. Один изспособов - представить каждое число в виде спискаего цифр. Например, число 255 будет тогдапредставляться списком [2, 2, 5]. Поскольку значенияцифр нам не известны заранее, каждая цифра будетобозначаться соответствующейнеинициализированной переменной. Используя этопредставление, мы можем сформулировать задачутак:

[ D, O, N, A, L, D ]

+ [ G, E, R, A, L, D ]

= [ R, О, B, E, R, T ]

Теперь задача состоит в том. чтобы найти такуюконкретизацию переменных D, О, N и т.д., для которойсумма верна. После того, как отношение суммабудет запрограммировано, задание дляпролог-системы на решение ребуса будет иметь вид

?- сумма( [D, O, N, A, L,D], [G, E, R, A, L, D],

[R, O, В, Е, R, T ).

Рис. 7. 1. Поразрядноесложение. Отношения в показанном i-м

разряде такие: D_3i = (C1 + D_1i+ D_2i) mod 10; C = (C1 +D_1i + D_2i)

div 10 (div - целочисленное деление, mod -остаток от деления).

Для определения отношения сумма надсписками цифр нам нужно запрограммироватьреальные правила суммирования в десятичнойсистеме счисления. Суммирование производитсяцифра за цифрой, начиная с младших цифр в сторонустарших, всякий раз учитывая цифру переносасправа. Необходимо также сохранять множестводопустимых цифр, т.е. цифр, которые еще не былииспользованы для конкретизации ужевстретившихся переменных. Поэтому, вообщеговоря, кроме трех чисел Nl, N2 и N в рассмотрениидолжна участвовать некоторая дополнительнаяинформация, как показано на рис. 7.1:

перенос перед сложением

перенос после сложения

множество цифр, доступных перед сложением

оставшиеся цифры, не использованные при сложении

Для формулировки отношения сумма мыснова воспользуемся принципом обобщения задачи:введем вспомогательное, более общее отношение сумма1.Это отношение будет иметь несколькодополнительных аргументов, соответствующих тойдополнительной информации, о которой говорилосьвыше:

сумма1( Nl, N2, N, C1, С,Цифры1, Цифры)

Здесь Nl, N2 и N - наши три числа, как и в отношениисумма, С1 - перенос справа (до сложения Nl и N2), а С -перенос влево (после сложения). Пример:

?- сумма1( [H, E], [6,E], [U, S], l, l,

[1, 3, 4, 7, 8, 9], Цифры ).

Н = 8

Е = 3

S = 7

U = 4

Цифры = [1, 9]

Если Nl и N удовлетворяют отношению сумма,то, как показано на рис. 7.1, С1 и С должны быть равны0. Цифры1 - список цифр, которые не былииспользованы для конкретизации переменных.Поскольку мы допускаем использование вотношении сумма любых цифр, ееопределение в терминах отношения сумма1выглядит так:

сумма( Nl, N2, N) :-

cyммa1( Nl, N2, N, 0, 0, [0, l, 2, 3, 4, 5, 6, 7, 8, 9], _ ).

Бремя решения задачи переложено теперь наотношение сумма1. Но это отношениеявляется уже достаточно общим, чтобы можно былоопределить его рекурсивно. Без ограниченияобщности мы предположим, что все три списка,представляющие три числа, имеют одинаковуюдлину. Наш пример, конечно, удовлетворяет этомуусловию, но если это не так, то всегда можноприписать слева нужное количество нулей к более"короткому" числу.

Определение отношения сумма1 можноразбить на два случая:

(1) Все три числапредставляются пустыми списками. Тогда

сумма1( [ ], [ ], [ ], 0, 0,Циф, Циф).

(2) Все три числа имеюткакую-то самую левую цифру и справа от нее -остальные цифры. То есть, они имеют вид:

[D1 | Nl], [D2 | N2], [D | N]

В этом случае должны выполняться два условия:

(а) Оставшиеся цифры,рассматриваемые как три числа Nl, N2 и N, сами должныудовлетворять отношению сумма1, выдаваявлево некоторый перенос С2 и оставляя некотороеподмножество неиспользованных цифр Циф2.

(b) Крайние левые цифры D1,D2 и D, а также перенос С2 должны удовлетворятьотношению, показанному на рис. 7.1: С2, D1 и D2складываются, давая в результате D и переносвлево. Это условие в нашей программеформулируется в виде отношения суммацифр.

Переводя это на Пролог, получаем:

сумма1( [D1 | N1], [D2 | N2],[D | N], С1, С, Циф1, Циф) :-

сумма1( Nl, N2, N, С1, С2, Циф1, Циф2),

суммацифр( D1, D2, С2, D, С, Циф2, Циф).

Осталось только описать на Прологе отношение суммацифр.В его определении есть одна тонкая деталь,касающаяся применения металогическогопредиката nonvar. D1, D2 и D должны бытьдесятичными цифрами. Если хоть одна из этихпеременных еще не конкретизирована, ее нужноконкретизировать какой-нибудь цифрой из списка Циф2.Как только такая конкретизация произошла, этуцифру нужно удалить из множества доступных цифр.Если D1, D2 и D уже конкретизированы, тогда, конечно,ни одна из доступных цифр "потрачена" небудет. В программе эти действия реализуются припомощи недетерминированного вычеркиванияэлемента списка. Если этот элемент - непеременная, ничего не вычеркивается(конкретизации не было). Вот эта программа:

удалить( Элемент,Список, Список) :-

nonvar( Элемент), !.

удалить( Элемент,[Элемент | Список ], Список).

удалить(Элемент, [А |Список], [А | Список1]) :-

удалить( Элемент, Список, Список1).

Полная программа для решения арифметическихребусов приводится на рис. 7.2. В программувключены также определения двух ребусов. Вопроск пролог-системе для ребуса про DONALD'a, GERALD'a и ROBERT'aс использованием этой программы выглядит так:

?- ребус1( N1, N2, N),сумма( N1, N2, N).

% Решение числовых ребусов

сумма( N1, N2, N) :-

% Числа представлены в виде списков цифр

сумма1( N1, N2, N,

0, 0,

% Перенос справа и перенос влево равны 0

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9], _ ).

% Все цифры доступны

сумма1( [ ], [ ], [ ], 0, 0, Цифры, Цифры).

сумма1( [D1 | N1], [D2 | N2], [D | N], C1, С, Циф1, Циф) :-

сумма1( Nl, N2, N, C1, C2, Циф1,Циф2),

суммацифр( Dl, D2, C2, С, Циф2,Циф).

суммацифр( Dl, D2, C1, D, С, Циф1, Циф) :-

удалить( D1, Циф1, Циф2),

% Выбор доступной цифры для D1

удалить( D2, Циф2, Циф3),

% Выбор доступной цифры для D2

удалить( D, Циф3, Циф),

% Выбор доступной цифры для D

S is D1 + D2 + C1,

D is S mod 10,

С is S div 10.

удалить( A, L, L) :-

nonvar( A), !.

% Переменная А уже конкретизирована

удалить( А, [А | L], L).

удалить( А, [В | L], [В | L1]) :-

удалить( A, L, L1).

% Примеры ребусов

ребус1( [D, O, N, A, L, D],

[G, E, R,A, L, D],

[R, O, B,E, R, T].

ребус2( [0, S, E, N, D],

[0, M, O,R, E],

[M, O, N,E, Y].

Рис. 7. 2. Программа дляарифметических ребусов.

Иногда этот ребус упрощают, сообщая частьрешения в виде дополнительного ограничения,например D равно 5. В такой форме ребус можнопередать пролог-системе при помощи сумма1:

? - сумма1( [5, O, N, A,L, 5],

[G,E, R, A, L, 5],

[R,O, B, E, R, T],

0,0, [0, 1, 2, 3, 4, 6, 7, 8, 9], _ ).

Интересно, что в обоих случаях существуеттолько одно решение, т.е. только один способзаменить буквы цифрами.

Упражнения

7. 1. Напишите процедуру упроститьдля упрощения алгебраических сумм, в которыхучаствуют числа и символы (строчные буквы). Пустьэта процедура переупорядочивает слагаемые так,чтобы символы предшествовали числам. Вот примерыее использования:

?- упростить( 1 + 1 +а, Е).

Е = а + 2

?- упростить( l + a +4 + 2 + b + с, E).

Е = а + b + с + 7

?- упростить( 3 + х+ х, Е).

Е = 2*х + 3

7. 2. Определите процедуру

добавить( Элемент,Список)

для добавления нового элемента в список.Предполагается, что все элементы, хранящиеся всписке, - атомы. Список состоит из всеххранящихся в нем элементов, а за ними следуетхвост, который не конкретизирован и служит дляпринятия новых элементов. Пусть, например, всписке уже хранятся а, b и с,тогда

Список = [а, b, с |Хвост]

где Хвост - переменная. Цель

добавить( d, Список)

вызовет конкретизацию

Xвoст = [d |НовыйХвост] и

Список = [а, b, с, d |НовыйХвост]

Таким способом структура может наращиваться,включая в себя новые элементы. Определите такжесоответствующее отношение принадлежности.

Посмотреть ответ

Назад | Содержание| Вперёд

Оглавление