Назад | Содержание| Вперёд 4. 5. Задача о восьми ферзях Эта задач...

Назад | Содержание| Вперёд

4. 5. Задача о восьми ферзях

Эта задача состоит в отыскании такойрасстановки восьми ферзей на пустой шахматнойдоске, в которой ни один из ферзей не находитсяпод боем другого. Решение мы запрограммируем ввиде унарного отношения:

решение( Поз)

которое истинно тогда и только тогда, когда Позизображает позицию, в которой восемь ферзей небьют друг друга. Будет интересно сравнитьразличные идеи, лежащие в основепрограммирования этой задачи. Поэтому мыприведем три программы, основанные на слегкаразличающихся ее представлениях.

4. 5. 1. Программа 1

Вначале нужно выбрать способ представленияпозиции на доске. Один из наиболее естественныхспособов - представить позицию в виде списка извосьми элементов, каждый из которыхсоответствует одному из ферзей. Каждый такойэлемент будет описывать то поле доски, на которойстоит соответствующий ферзь. Далее, каждое поледоски можно описать с помощью пары координат ( Х иY), где каждая координата - целое число от 1 до 8. Впрограмме мы будем записывать такую пару в виде

Х / Y

где оператор "/" обозначает, конечно, неделение, а служит лишь для объединения координатполя в один элемент списка. На рис. 4.6 показаноодно из решений задачи о восьми ферзях и егозапись в виде списка.

После того. как мы выбрали такое представление,задача свелась к нахождению списка вида:

[Xl/Yl, X2/Y2, X3/Y3, X4/Y4, X5/Y5,X6/Y6, X7/Y7, X8/Y8]

удовлетворяющего требованию отсутствиянападений. Наша процедура решениедолжна будет найти подходящую конкретизациюпеременных X1, Y1, Х2, Y2,..., Х8, Y8. Поскольку мызнаем, что все ферзи должны находиться на разныхвертикалях во избежание нападений повертикальным линиям, мы можем сразу жеограничить перебор, чтобы облегчать поискрешения. Можно поэтому сразу зафиксироватьХ-координаты так, чтобы список, изображающийрешение, удовлетворял следующему, болееконкретному шаблону:

[1/Y1, 2/Y2, 3/Y3, 4/Y4, 5/Y5, 6/Y6,7/Y7, 8/Y8]

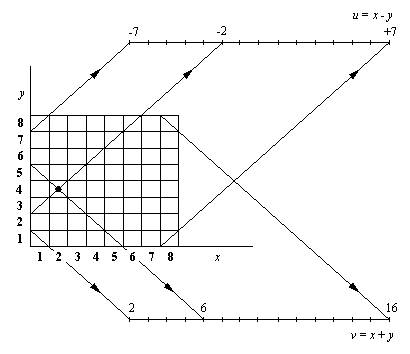
Рис. 4. 10. Связь междувертикалями, горизонталями и диагоналями. Помеченное

поле имеет следующие координаты: x= 2, у = 4, u = 2 - 4 = -2, v = 2 + 4 = 6.

Области изменения всех четырех координаттаковы:

Dx = [1, 2, 3, 4, 5, 6, 7, 8]

Dy = [1, 2, 3, 4, 5, 6, 7, 8]

Du = [-7, -6, -5, -4, -3, -2, -1, 0,1, 2, 3, 4, 5, 6, 7]

Dv = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,14, 15, 16]

Задачу о восьми ферзях теперь можносформулировать следующим образом: выбратьвосемь четверок (X, Y, U, V), входящих в областиизменения (X в Dx, Y в Dy и т.д.), так, чтобы ни один ихэлемент не выбирался дважды из одной области.Разумеется, выбор Х и Y определяет выбор U и V.Решение при такой постановке задачи может бытьвкратце таким: при заданных 4-х областяхизменения выбрать позицию для первого ферзя,вычеркнуть соответствующие элементы из 4-хобластей изменения, а затем использоватьоставшиеся элементы этих областей дляразмещения остальных ферзей. Программа,основанная на таком подходе, показана на рис. 4.11.Позиция на доске снова представляется спискомY-координат. Ключевым отношением в этой программеявляется отношение

peш( СписY, Dx, Dy, Du, Dv)

которое конкретизирует Y-координаты (в СписY)ферзей, считая, что они размещены впоследовательных вертикалях, взятых из Dx. ВсеY-координаты и соответствующие координаты U и Vберутся из списков Dy, Du и Dv. Главную процедуру решениеможно запустить вопросом

?- решение( S)

Это вызовет запуск реш с полнымиобластями изменения координат, чтосоответствует пространству

решение( СписY) :-

реш( СписY, % Y-координаты ферзей

[1, 2, 3, 4, 5, 6, 7, 8],

% Область изменения Y-координат

[1, 2, 3, 4, 5, 6, 7, 8],

% Область изменения Х-координат

[-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7],

% Диагонали, идущие снизу вверх

[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 14, 15, 16] ).

% Диагонали, идущие сверху вниз

реш([ ], [ ], Dy, Du, Dv).

реш( [Y | СписY], [X | Dx1], Dy, Du, Dv) :-

удалить( Y, Dy, Dy1), % ВыборY-координаты

U is X-Y % Соответствующая диагональ вверх

удалить( U, Du, Du1), % Ееудаление

V is X+Y % Соответствующая диагональ вниз

удалить( V, Dv, Dv1), % Ееудаление

реш( СписY, Dх1, Dy1, Du1,Dv1).

% Выбор из оставшихся значений

удалить( А, [А | Список], Список).

удалить(A, [В | Список ], [В | Список1 ] ) :-

удалить( А, Список,Список1).

Рис. 4. 11. Программа 3 длязадачи о восьми ферзях.

задачи о восьми ферзях.

Процедура реш универсальна в томсмысле, что ее можно использовать для решениязадачи об N ферзях (на доске размером N х N). Нужнотолько правильно задеть области Dx, Dy и т.д.

Удобно автоматизировать получение этихобластей. Для этого нам потребуется процедура

генератор( Nl, N2,Список)

которая для двух заданных целых чисел Nl и N2порождает список

Список = [Nl, Nl + 1, Nl + 2,..., N2 - 1, N2]

Вот она:

генератор( N, N, [N]).

генератор( Nl, N2, [Nl |Список]) :-

Nl < N2,

М is Nl + 1,

генератор( М, N2, Список).

Главную процедуру решение нужносоответствующим образом обобщить:

решение( N, S)

где N - это размер доски, а S - решение,представляемое в виде списка Y-координат N ферзей.Вот обобщенное отношение решение:

решение( N, S) :-

генератор( 1, N, Dxy),

Nu1 is 1 - N, Nu2 is N - 1,

генератор( Nu1, Nu2, Du),

Nv2 is N + N,

генератор( 2, Nv2, Dv),

реш( S, Dxy, Dxy, Du, Dv).

Например, решение задачи о 12 ферзях будетполучено с помощью:

?- решение( 12, S).

S = [1, 3, 5, 8, 10, 12, 6, 11, 2,7, 9, 4]

4. 5. 4. Заключительные замечания

Три решения задачи о восьми ферзях показывают,как к одной и той же задаче можно применятьразличные подходы. Мы варьировали также ипредставление данных. В одних случаях этопредставление было более экономным, в других -более наглядным и, до некоторой степени,избыточным. К недостаткам более экономногопредставления можно отнести то, что какая-тоинформация всякий раз, когда она требовалась,должна была перевычисляться.

В некоторых случаях основным шагом к решениюбыло обобщение задачи. Как ни парадоксально, нопри рассмотрении более общей задачи решениеоказывалось проще сформулировать. Принциптакого обобщения - стандартный приемпрограммирования, и его можно часто применять.

Из всех трех программ третья лучше всегопоказывает, как подходить к общей задачепостроения структуры из заданного множестваэлементов при наличии ограничений.

Возникает естественный вопрос: " Какая изтрех программ наиболее эффективна?" В этомотношение программа 2 значительно хуже двухдругих, а эти последние - одинаковы. Причина в том,что основанная на перестановках программа 2строит все перестановки, тогда как две другиепрограммы способны отбросить плохуюперестановку не дожидаясь, пока она будетполностью построена. Программа 3 наиболееэффективна. Она избегает некоторыхарифметических вычислений, результаты которыхуже сразу заложены в избыточное представлениедоски, используемое этой программой.

Упражнение

4. 7. Пусть поля доскипредставлены парами своих координат в виде X/Y,где как X, так и Y принимают значения от 1 до 8.

(а) Определите отношение ходконя(Поле1, Поле2), соответствующее ходу коня нашахматной доске. Считайте, что Поле1имеет всегда конкретизированные координаты, в товремя, как координаты поля Поле2 могут ине быть конкретизированы. Например:

?- ходконя( 1/1, S).

S = 3/2;

S = 2/3;

no (нет)

(b) Определите отношение путьконя(Путь), где Путь - список полей,представляющих соответствующую правилам игрыпоследовательность ходов коня по пустой доске.

(с) Используя отношение путьконя,напишите вопрос для нахождения любого пути,состоящего из 4-х ходов, и начинающегося с поля 2/1,а заканчивающегося на противоположном краедоски (Y= 8). Этот путь должен еще проходить послевторого хода через поле 5/4.

Посмотреть ответ

Резюме

Примеры, рассмотренные в данном разделе,иллюстрируют некоторые достоинства ихарактерные черты программирования на Прологе:

Базу данных можно естественным образом представить в виде множества прологовских фактов.

Такие механизмы Пролога, как вопросы и сопоставление, можно гибко использовать для получения информации из базы данных. Кроме этого можно использовать вспомогательные процедуры-утилиты, еще больше облегчающие взаимодействие с конкретной базой данных.

Абстракцию данных можно рассматривать как метод программирования, который облегчает работу со сложными структурами данных и вносит большую ясность и наглядность в программы. В Прологе легко соблюдать основные принципы абстракции данных.

Часто легко можно осуществить перевод абстрактных математических конструкций, таких как автоматы, на язык определений Пролога, готовых к выполнению.

Как это было в случае восьми ферзей, многие задачи допускают различные подходы, связанные с разными представлениями этих задач. Часто внесение избыточности в представление экономит вычисления. Происходит как бы проигрыш в рабочем пространстве, но выигрыш во времени.

Часто основным шагом на пути к решению оказывается обобщение задачи. Парадоксально, но рассмотрение более общей задачи позволяет облегчить формулировку решения.

Назад | Содержание| Вперёд

Оглавление