Назад | Содержание| Вперёд 4. 3. Моделированиенедетерминированного автомата...

Назад | Содержание| Вперёд

4. 3. Моделированиенедетерминированного автомата

Данное упражнение показывает, как абстрактнуюматематическую конструкцию можно представить наПрологе. Кроме того, программа, котораяполучится, окажется значительно более гибкой,чем предполагалось вначале.

Недетерминированный конечныйавтомат - это абстрактная машина, котораячитает символы из входной цепочки и решает, допуститьили отвергнуть эту цепочку. Автомат имеетнесколько состояний и всегда находится водном из них. Он может изменить состояние,перейдя из одного состояния в другое. Внутреннююструктуру такого автомата можно представитьграфом переходов, как показано на рис. 4.3. В этомпримере S₁, S₂, S₃ и S₄ - состояния автомата.Стартовав из начального состояния (в нашемпримере это S₁ ), автомат переходит изсостояния в состояние по мере чтения входнойцепочки. Переход зависит от текущего входногосимвола, как указывают метки на дугах графапереходов.

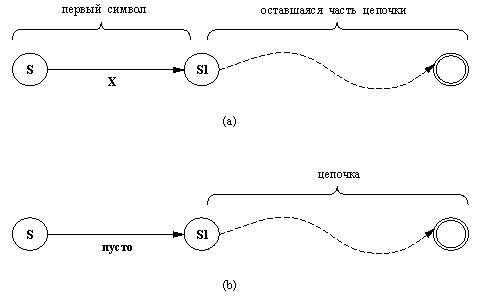
Рис. 4. 4. Допущениецепочки: (a) при чтении первогосимвола X;

(b) при совершении спонтанногоперехода.

текущем состоянии. Однако абстрактныенедетерминированные машины такого типа обладаютволшебным свойством: если существует выбор, онивсегда избирают "правильный" переход, т.е.переход, ведущий к допущению входной цепочки приналичии такого перехода. Автомат на рис. 4.3,например, допускает цепочки аb и aabaab, но отвергает цепочки abb и abba. Легко видеть, что этот автомат допускаетлюбые цепочки, оканчивающиеся на аb иотвергает все остальные.

Некоторый автомат можно описать на Прологе припомощи трех отношений:

(1) Унарного отношения конечное,которое определяет конечное состояние автомата.

(2) Трехаргументногоотношения переход, которое определяетпереход из состояния в состояние, при этом

переход( S1, X, S2)

означает переход из состояния S1 в S2, если считанвходной символ X.

(3) Бинарного отношения

спонтанный( S1, S2)

означающего, что возможен спонтанный переходиз S1 в S2.

Для автомата, изображенного на рис. 4.3, этиотношения будут такими:

конечное( S3).

переход( S1, а, S1).

переход( S1, а, S2).

переход( S1, b, S1).

переход( S2, b, S3).

переход( S3, b, S4).

спонтанный( S2, S4).

спонтанный( S3, S1).

Представим входные цепочки в виде списковПролога. Цепочка ааb будетпредставлена как [а, а, b]. Модельавтомата, получив его описание, будетобрабатывать заданную входную цепочку, и решать,допускать ее или нет. По определению,недетерминированный автомат допускает заданнуюцепочку, если (начав из начального состояния)после ее прочтения он способен оказаться вконечном состоянии. Модель программируется ввиде бинарного отношения допускается,которое определяет принятие цепочки из данногосостояния. Так

допускается(Состояние, Цепочка)

истинно, если автомат, начав из состояния Состояниекак из начального, допускает цепочку Цепочка.Отношение допускается можно определитьпри помощи трех предложений. Они соответствуютследующим трем случаям:

(1) Пустая цепочка [ ]допускается из состояния S, если S - конечноесостояние.

(2) Непустая цепочкадопускается из состояния S, если после чтенияпервого ее символа автомат может перейти всостояние S1, и оставшаяся часть цепочкидопускается из S1. Этот случай иллюстрируется нарис. 4.4(а).

(3) Цепочка допускаетсяиз состояния S, если автомат может сделатьспонтанный переход из S в S1, а затем допустить(всю) входную цепочку из S1. Такой случайиллюстрируется на рис. 4.4(b).

Эти правила можно перевести на Прологследующим образом:

допускается( S, [ ]) :-

% Допуск пустой цепочки

конечное(S).

допускается( S, [X |Остальные]) :-

% Допуск чтением первого символа

переход(S, X, S1),

допускается( S1, Остальные).

допускается( S,Цепочка) :-

% Допуск выполнением спонтанного перехода

спонтанный(S, S1),

допускается( S1, Цепочка).

Спросить о том, допускается ли цепочка аааb, можно так:

?- допускается( S1,[a, a, a, b]).

yes (да)

Как мы уже видели, программы на Прологе частооказываются способными решать более общиезадачи, чем те, для которых они первоначальнопредназначались. В нашем случае мы можемспросить модель также о том, в каком состояниидолжен находиться автомат в начале работы, чтобыон допустил цепочку аb:

?- допускается( S,[a, b]).

S = s1;

S = s3

Как ни странно, мы можем спросить также"Каковы все цепочки длины 3, допустимые изсостояния s1?"

?- допускается( s1,[XI, Х2, X3]).

X1 = а

Х2 = а

Х3 = b;

X1 = b

Х2 = а

Х3 = b;

nо (нет)

Если мы предпочитаем, чтобы допустимые цепочкивыдавались в виде списков, тогда наш вопросследует сформулировать так:

?- Цепочка = [ _, _, _ ],допускается( s1, Цепочка).

Цепочка = [а, а, b];

Цепочка = [b, а, b];

nо (нет)

Можно проделать и еще некоторые эксперименты,например спросить: "Из какого состоянияавтомат допустит цепочку длиной 7?"

Эксперименты могут включать в себя переделкиструктуры автомата, вносящие изменения вотношения конечное, переход и спонтанный.В автомате, изображенном на рис. 4.3, отсутствуютциклические "спонтанные пути" (пути,состоящие только из спонтанных переходов). Еслина рис. 4.3 добавить новый переход

спонтанный( s1, s3)

то получится "спонтанный цикл". Теперьнаша модель может столкнуться с неприятностями.Например, вопрос

?- допускается( s1,[а]).

приведет к тому, что модель будет бесконечнопереходить в состояние s1, все время надеясьотыскать какой-либо путь в конечное состояние.

Упражнения

4. 4. Почему не могловозникнуть зацикливание модели исходногоавтомата на рис. 4.3, когда в его графе переходов небыло "спонтанного цикла"?

Посмотреть ответ

4. 5. Зацикливание привычислении допускается можнопредотвратить, например, таким способом:подсчитывать число переходов, сделанных кнастоящему моменту. При этом модель должна будетискать пути только некоторой ограниченной длины.Модифицируйте так отношение допускается.Указание: добавьте третий аргумент - максимальнодопустимое число переходов:

допускается(Состояние, Цепочка, Макс_переходов)

Посмотреть ответ

Назад | Содержание| Вперёд

Оглавление