Назад | Содержание| Вперёд 3. 2. Некоторые операции над списками ...

Назад | Содержание| Вперёд

3. 2. Некоторые операции над списками

Списки можно применять для представлениямножеств, хотя и существует некоторое различиемежду этими понятиями: порядок элементовмножества не существенен, в то время как длясписка этот порядок имеет значение; кроме того,один н тот же объект может встретиться в спискенесколько раз. Однако наиболее частоиспользуемые операции над списками аналогичныоперациям над множествами. Среди них

проверка, является ли некоторый объект элементом списка, что соответствует проверке объекта на принадлежность множеству;

конкатенация (сцепление) двух списков, что соответствует объединению множеств;

добавление нового объекта в список или удаление некоторого объекта из него.

В оставшейся части раздела мы покажемпрограммы, реализующие эти и некоторые другиеоперации над списками.

3. 2. 1. Принадлежность ксписку

Мы представим отношение принадлежности как

принадлежит( X, L)

где Х - объект, а L - список. Цель принадлежит(X, L) истинна, если элемент Х встречается в L.Например, верно что

принадлежит( b, [а, b,с] )

и, наоборот, не верно, что

принадлежит b, [а, [b,с] ] )

но

принадлежит [b, с], [а,[b, с]] )

истинно. Составление программы для отношенияпринадлежности может быть основано на следующихсоображениях:

(1) Х естьголова L, либо

(2) Хпринадлежит хвосту L.

Это можно записать в виде двух предложений,первое из которых есть простой факт, а второе -правило:

принадлежит( X, [X |Хвост ] ).

принадлежит ( X,[Голова | Хвост ] ) :-

принадлежит( X, Хвост).

3. 2. 2. Сцепление (конкатенация)

Для сцепления списков мы определим отношение

конк( L1, L2, L3)

Здесь L1 и L2 - два списка, a L3 - список, получаемыйпри их сцеплении. Например,

конк( [а, b], [c, d], [a, b, c,d] )

истинно, а

конк( [а, b], [c, d], [a, b, a,c, d] )

ложно. Определение отношения конк, каки раньше, содержит два случая в зависимости отвида первого аргумента L1:

(1) Если первый аргументпуст, тогда второй и третий аргументыпредставляют собой один и тот же список (назовемего L), что выражается в виде следующегопрологовского факта:

конк( [ ], L, L ).

(2) Если первый аргументотношения конк не пуст, то он имеетголову и хвост в выглядит так:

[X | L1]

На рис. 3.2 показано, как производится сцеплениесписка [X | L1] с произвольным списком L2.Результат сцепления - список [X | L3], где L3получен после сцепления списков L1 и L2. На прологеэто можно записать следующим образом:

конк( [X | L1, L2, [X | L3]):-

конк(L1, L2, L3).

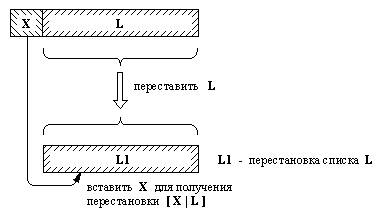
Рис. 3. 5. Один изспособов построения перестановки списка [X |L].

Программа для отношения перестановкав свою очередь опять может основываться нарассмотрении двух случаев в зависимости от видапервого списка:

(1) Если первый списокпуст, то и второй список должен быть пустым.

(2) Если первый список непуст, тогда он имеет вид [Х | L], и перестановкутакого списка можно построить так, как Этопоказано на рис. 3.5: вначале получить список L1 -перестановку L, а затем внести Х в произвольнуюпозицию L1.

Два прологовских предложения, соответствующихэтим двум случаям, таковы:

перестановка( [ ], [ ]).

перестановка( [X | L ],Р) :-

перестановка( L, L1),

внести( X, L1, Р).

Другой вариант этой программы мог быпредусматривать удаление элемента Х из первогосписка, перестановку оставшейся его части -получение списка Р, а затем добавление Х в началосписка Р. Соответствующая программа такова:

перестановка2( [ ], []).

перестановка2( L, [X |Р] ) :-

удалить( X, L, L1),

перестановка2( L1, Р).

Поучительно проделать несколько экспериментовс нашей программой перестановки. Ее нормальноеиспользование могло бы быть примерно таким:

?- перестановка([красный, голубой, зеленый], Р).

Как и предполагалось, будут построены все шестьперестановок:

Р = [ красный,голубой, зеленый];

Р = [ красный, зеленый,голубой];

Р = [ голубой, красный,зеленый];

Р = [ голубой, зеленый,красный];

Р = [ зеленый, красный,голубой];

Р = [ зеленый, голубой,красный];

nо (нет)

Приведем другой вариант использованияпроцедуры перестановка:

?- перестановка(L, [а, b, с] ).

Наша первая версия, перестановка,произведет успешную конкретизацию L всеми шестьюперестановками. Если пользователь потребуетновых решений, он никогда не получит ответ"нет", поскольку программа войдет вбесконечный цикл, пытаясь отыскать новыенесуществующие перестановки. Вторая версия, перестановка2,в этой ситуации найдет только первую (идентичную)перестановку, а затем сразу зациклится.Следовательно, при использовании этих отношенийтребуется соблюдать осторожность.

Упражнения

3. 3. Определите два предиката

четнаядлина(Список) и нечетнаядлина(Список)

таким образом, чтобы они были истинными, если ихаргументом является список четной или нечетнойдлины соответственно. Например, список [а, b, с, d]имеет четную длину, a [a, b, c] - нечетную.

Посмотреть ответ

3. 4. Определите отношение

обращение( Список,ОбращенныйСписок),

которое обращает списки. Например,

обращение( [a, b, c, d],[d, c, b, a] ).

Посмотреть ответ

3. 5. Определите предикат

палиндром( Список).

Список называется палиндромом, если ончитается одинаково, как слева направо, так исправа налево. Например, [м, а, д, а, м].

Посмотреть ответ

3. 6. Определите отношение

сдвиг( Список1,Список2)

таким образом, чтобы Список2представлял собой Список1,"циклически сдвинутый" влево на один символ.Например,

?- сдвиг( [1, 2, 3, 4,5], L1),

сдвиг1( LI,L2)

дает

L1 = [2, 3, 4, 5, 1]

L2 = [3, 4, 5, 1, 2]

Посмотреть ответ

3. 7. Определите отношение

перевод( Список1,Список2)

для перевода списка чисел от 0 до 9 в списоксоответствующих слов. Например,

перевод( [3, 5, 1, 3],[три, пять, один, три] )

Используйте в качестве вспомогательныхследующие отношения:

означает( 0, нуль).

означает( 1, один).

означает( 2, два).

. . .

Посмотреть ответ

3. 8. Определитеотношение

подмножество(Множество, Подмножество)

где Множество и Подмножество- два списка представляющие два множества.Желательно иметь возможность использовать этоотношение не только для проверки включенияодного множества в другое, но и для порождениявсех возможных подмножеств заданного множества.Например:

?- подмножество([а, b, с], S ).

S = [a, b, c];

S = [b, c];

S = [c];

S = [ ];

S = [a, c];

S = [a];

. . .

Посмотреть ответ

3. 9. Определите отношение

разбиениесписка(Список, Список1, Список2)

так, чтобы оно распределяло элементы спискамежду двумя списками Список1 и Список2и чтобы эти списки были примерно одинаковойдлины. Например:

разбиениесписка( [а,b, с, d, e], [a, с, е], [b, d]).

Посмотреть ответ

3. 10. Перепишите программу обобезьяне и бананах из главы 2 таким образом, чтобыотношение

можетзавладеть(Состояние, Действия)

давало не только положительный илиотрицательный ответ, но и порождалопоследовательность действий обезьяны,приводящую ее к успеху. Пусть Действиябудет такой последовательностью, представленнойв виде списка ходов:

Действия = [ перейти(дверь, окно),

передвинуть( окно, середина),

залезть, схватить ]

Посмотреть ответ

3. 11. Определите отношение

линеаризация(Список, ЛинейныйСписок)

где Список может быть списком списков,а ЛинейныйСписок - это тот же список, но"выровненный" таким образом, что элементыего подсписков составляют один линейный список.Например:

? - линеаризация( [а,d, [с, d], [ ], [[[е]]], f, L).

L = [a, b, c, d, e, f]

Посмотреть ответ

Назад | Содержание| Вперёд

Оглавление