Назад | Содержание| Вперёд 2. 2. Сопоставление В предыдущем разде...

Назад | Содержание| Вперёд

2. 2. Сопоставление

В предыдущем разделе мы видели, какиспользуются термы для представления сложныхобъектов данных. Наиболее важнойоперацией над термами является сопоставление.Сопоставление само по себе может производитьсодержательные вычисления.

Пусть даны два терма. Будем говорить, что они сопоставимы,если:

(1) они идентичны или

(2) переменным в обоих термах можноприписать в качестве значений объекты (т.е.конкретизировать их) таким образом, чтобы послеподстановки этих объектов в термы вместопеременных, последние стали идентичными.

Например, термы дата( Д, М, 1983) и дата(Д1, май, Y1) сопоставимы. Одной изконкретизации, которая делает эти термыидентичными, является следующая:

Д заменяется на Д1

М заменяется на май

Y1 заменяется на 1983

Более компактно такая подстановказаписывается в привычной форме, т. е. в той, вкоторой пролог-система выводит результаты:

Д = Д1

М = май

Y1 = 1983

С другой стороны, дата( Д, М, 1983) и дата(Д1, Ml, 1944) не сопоставимы, как и термы дата(X, Y, Z) и точка( X, Y, Z).

Сопоставление - это процесс,на вход которого подаются два терма, а онпроверяет, соответствуют ли эти термы друг другу.Если термы не сопоставимы, будем говорить, чтоэтот процесс терпит неуспех. Если же онисопоставимы, тогда процесс находитконкретизацию переменных, делающую эти термытождественными, и завершается успешно.

Рассмотрим еще раз сопоставление двух дат.Запрос на проведение такой операции можнопередать системе, использовав оператор '=':

?- дата( Д, М, 1983) = дата( Д1, май, Y1).

Мы уже упоминали конкретизацию Д = Д1,М = май, Y1 = 1983,на которой достигается сопоставление.Существуют, однако, и другие конкретизации,делающие оба терма идентичными. Вот две из них:

Д = 1

Д1 = 1

М = май

Y1 = 1983

Д = третий

Д1 = третий

М = май

Y1 = 1983

Говорят, что эти конкретизации являются менееобщими по сравнению с первой, поскольку ониограничивают значения переменных Д и Д1в большей степени, чем это необходимо. Для того,чтобы сделать оба терма нашего примераидентичными, важно лишь, чтобы Д и Д1имели одно и то же значение, однако

самоэто значение может быть произвольным.

Сопоставлениев Прологе всегда дает

наиболее общуюконкретизацию

. Таковой являетсяконкретизация, которая ограничивает переменныев наименьшей степени, оставляя им, тем самым,наибольшую свободу для дальнейшихконкретизаций, если потребуются новыесопоставления. В качестве примера рассмотримследующий вопрос:

?- дата( Д, М, 1983) = дата( Д1, май, Y1),

дата( Д, М,1983) = дата( 15, М, Y).

Для достижения первой цели система припишетпеременным такие значения:

Д = Д1

М = май

Y1 = 1983

После достижения второй цели, значенияпеременных станут более конкретными, а именно:

Д = 15

Д1 = 15

М = май

Y1 = 1983

Y = 1983

Этот пример иллюстрирует также и тот факт, чтопеременным по мере вычисленияпоследовательности целей приписываются обычновсе более и более конкретные значения.

Общие правила выяснения, сопоставимы ли дватерма S и Т, таковы:

(1) Если S и Т - константы, то S и Тсопоставимы, только если они являются одним и темже объектом.

(2) Если S - переменная, а Т -произвольный объект, то они сопоставимы, и Sприписывается значение Т. Наоборот, если Т-переменная, а S -произвольный объект, то Тприписывается значение S.

(3) Если S и Т - структуры, то онисопоставимы, только если

(а) S и Т имеют одинаковый главныйфунктор

(б) все их соответствующие компонентысопоставимы.

Результирующаяконкретизация определяется сопоставлениемкомпонент.

Последнее из этих правил можно нагляднопредставить себе, рассмотрев древовидноеизображение термов, такое, например, как на рис.2.7. Процесс сопоставления начинается от корня(главных функторов). Поскольку оба функторасопоставимы, процесс продолжается исопоставляет соответствующие пары аргументов.Таким образом, можно представить себе, что весьпроцесс сопоставления состоит из следующейпоследовательности (более простых) операцийсопоставления:

треугольник = треугольник,

точка( 1, 1) = X,

А = точка( 4, Y),

точка( 2, 3) = точка( 2,Z).

Весь процесс сопоставления успешен, посколькувсе сопоставления в этой последовательностиуспешны. Результирующая конкретизация такова:

Х = точка( 1, 1)

А = точка( 4, Y)

Z = 3

В приведенном ниже примере показано, каксопоставление само по себе можно использоватьдля содержательных вычислений. Давайте вернемсяк простым геометрическим объектам с рис. 2.4 инапишем фрагмент программы для распознаваниягоризонтальных и вертикальных отрезков."Вертикальность" - это свойство отрезка,поэтому его можно формализовать в Прологе в видеунарного отношения. Рис. 2.8 помогаетсформулировать это отношение. Отрезок

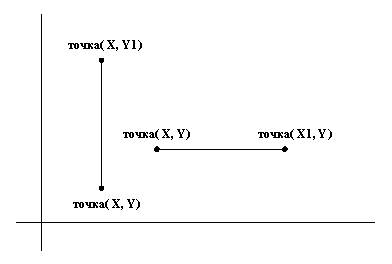
Рис. 2. 8. Примервертикальных и горизонтальных отрезков прямых.

Сформулируем более общий вопрос к программе:"Существуют ли какие-либо вертикальныеотрезки, начало которых лежит в точке (2,3)?"

?- верт(отр( точка( 2, 3), Р) ).

Р = точка( 2, Y)

Такой ответ означает: "Да, это любой отрезок,с концом в точке (2,Y), т. е. в произвольной точкевертикальной прямой х = 2". Следуетзаметить, что ответ пролог-системы возможнобудет выглядеть не так красиво, как только чтоописано, а (в зависимости от реализации)приблизительно следующим образом:

Р = точка( 2, _136)

Впрочем, разница здесь чисто внешняя. В данномслучае _136 - это неинициализированнаяпеременная. Имя _136 - законное имяпрологовской переменной, которое системапостроила сама во время вычислений. Ейприходится генерировать новые имена, для тогочтобы переименовывать введенные пользователемпеременные в программе. Это необходимо по двумпричинам: первая - одинаковые имена обозначают вразных предложениях разные переменные; и вторая -при последовательном применении одного и того жепредложения используется каждый раз его"копия" с новым набором переменных.

Другим содержательным вопросом к нашейпрограммe является следующий: "Существует лиотрезок, который одновременно и горизонтален ввертикален?"

?- верт( S),гор( S).

S = отр( точка( Х, Y),точка( Х, Y) )

Такой ответ пролог-системы следует, пониматьтак: "да, любой отрезок, выродившийся в точку,обладает как свойством вертикальности, так исвойством горизонтальности одновременно".Этот ответ снова получен лишь из сопоставления.Как и раньше, в ответе вместо Х и Y могут появитьсянекоторые имена, сгенерированные системой.

Упражнения

2. 3. Будут ли следующиеоперации сопоставления успешными илинеуспешными? Если они будут успешными, то каковабудет результирующая конкретизация переменных?

(а) точка(А, В) = точка( 1, 2)

(b) точка( А,В) = точка( X, Y, Z)

(d) +( 2, D)= +( Е,2)

(е) треугольник(точка( -1, 0), Р2, Р3) =

треугольник( Р1, точка( 1, 0), точка( 0, Y)

Результирующая конкретизация определяетсемейство треугольников. Как бы Вы описали этосемейство?

Посмотреть ответ

2. 4 Используя представлениеотрезков, применявшееся в данной разделе,напишите терм, соответствующий любому отрезку навертикальной прямой x = 5.

Посмотреть ответ

2. 5. Предположим, чтопрямоугольник представлен термом прямоугольник(P1, P2, P3, Р4), где Р - вершиныпрямоугольника, положительно упорядоченные.Определите отношение

регулярный( R)

которое имеет место, если R - прямоугольник свертикальными и горизонтальными сторонами.

Посмотреть ответ

Назад | Содержание| Вперёд

Оглавление