|
||||
|
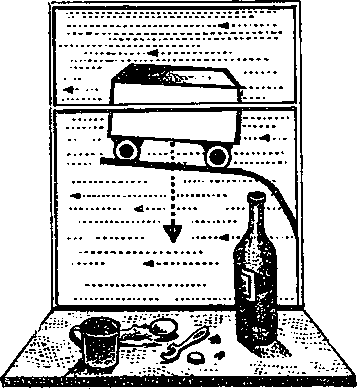
Часть третья УДИВЛЕНИЕ ТЯГОТЕНИЮ Глава 17. КАК ИЗГОТОВИТЬ ТЯЖЕСТЬ Еще воспоминание и обещаниеВы не забыли, от какого удивления мы намеревались убежать в начале этой книжки? От удивления падению. Падению ядер, пуль, пушинок. Нам очень хотелось понять внутреннюю сущность земного тяготения: как это оно действует через пустоту, почему одинаково ускоряет тела разного веса? Мы, кажется, довольно скоро поняли, что задача не из легких. На вопрос «Почему тяготение действует через пустоту?» ответа не нашлось. На вопрос «Почему тополиная пушинка и пушечное ядро в безвоздушной среде получают от тяготения равные ускорения?» ответ был добыт, но не очень вразумительный. Пришлось допустить, что во всяком теле существуют две массы — тяжелая и инертная и что они с беспредельной, абсолютной точностью одинаковы. Равенство тяжелой и инертной масс выглядело в физике Ньютона чистой случайностью. Отсюда следовал неправдоподобный вывод: космический порядок звездных и планетных движений, весь гармоничный хоровод светил держится на совпадении! Удивительно! Просто невероятно! Дабы убежать от этого удивления, мы углубились в физику. Разобрались в странностях распространения света, через серию промежуточных удивлений проникли в мир Эйнштейна, дошли до относительности времени, расстояний, до великого закона эквивалентности массы и энергии. По ходу дела мы без стеснения пользовались, если было нужно, равенством тяжелой и инертной масс. Но этим вносили, как по аналогичному поводу выражался Эйнштейн, натяжку в рассуждении, ибо старое сомнение отнюдь не было разрешено. Все разговоры о том, что энергия имеет вес, вытекают из замены инертной массы на тяжелую. А это и есть натяжка. И вот я с радостью сообщаю вам: настало время избавиться от недоумений по поводу «случайного» равенства тяжелой и инертной масс. Мы уже почти готовы к обсуждению внутренней сущности тяготения, готовы к заключительному этапу бегства от удивления одинаковой быстроте падения мельничных жерновов и тополиных пушинок. И даже от удивления «действию без прикосновения». Все эти простые и вместе с тем фантастически сложные загадки решаются в тонкой и глубокой области современного физического знания, которая именуется общей теорией относительности. Она охватила универсальным принципом относительности не только равномерные и прямолинейные, но и ускоренные движения, и гравитационные явления. В ней признаются законными, годными для физики, все системы отсчета, а не только инерциальные. Общая теория, опубликованная Эйнштейном в 1916 году, сразу привлекла к себе пристальное внимание. Ее широта и смелость поразили физиков еще больше, чем парадоксальная новизна частной теории[12]. Поныне существует мнение, что общая теория обогнала естественный прогресс науки (об этом говорил и сам Эйнштейн). Поныне вокруг нее не смолкают споры, строятся разные толкования ее идей. Сотая ОлимпиадаСотые Олимпийские игры будут в 2292 году. Это я рассчитал точно по календарю. Но где их проведут? Тут — целая проблема. Очень может быть, что по этому вопросу в организационном комитете произойдет оживленная дискуссия, а то и перепалка. Обитатели Земли захотят, чтобы игры состоялись на Земле. Жители Луны предложат, естественно, Луну; марсиане — Марс, венериане — Венеру и т. д. К тому времени люди или созданные ими роботы (не уступающие, быть может, человеку в спортивном мастерстве) поселятся на многих планетах Солнечной системы, и всякий будет звать к себе олимпийских гостей, потому что, я думаю, настанет эра всеобщего гостеприимства. И еще потому, что на родной планете бегать, прыгать и играть в разные подвижные игры удобнее, чем на чужой— хотя бы из-за привычной силы тяжести. Лунному жителю на Земле в шесть раз труднее двигаться, чем у себя дома. Как же решится спор? Как помирить противоречия и соблюсти равноправие участников? Где состоятся игры? Из сегодняшней старины, за 325 лет до Олимпиады № 100, я решусь дать совет членам подготовительного комитета: лучше всего, уважаемые прапрапраправнуки, если вы организуете игры на нейтральной территории, свободной от вещества, — где-нибудь в космосе, причем подальше от планет и Солнца. Я слышу из будущего сердитое возражение: Но в космосе нет тяжести! Как же без тяжести прыгать, бегать, поднимать штанги? Тяжесть можно изготовить, уверяю вас. Любую, и сильную и слабую, на всякий вкус, по потребностям каждого спортсмена — и селенита, и марсианина, и землянина. Как это «изготовить»? Что еще за тяжесть без земного, лунного, солнечного притяжения? Подделку, наверное, предлагаете? Никакую не подделку. Не суррогат, не фальсификацию, а самую настоящую тяжесть. На следующих страницах я берусь убедить вас, что это вполне возможно, и объясню, какие потребуются технические средства. Ну ладно, объясняйте, — говорят мне прапрапраправнуки, члены подготовительного комитета сотых Олимпийских игр. Возражения и реплики из будущего были посланы, надо полагать, со скоростью, превышающей скорость света, — поэтому и прибыли ко мне на триста с лишним лет раньше, чем были посланы. А так как сие невозможно, то приведенный выше разговор мне, надо полагать, приснился или померещился. Тем более, что через триста лет сведения, которые я намереваюсь сообщить ниже, будут наверное, известны школьникам третьего класса. Тяжесть проще табуреткиВы знаете, что такое кухонная табуретка? Вероятно, знаете. А как вы докажете, что знаете? Можно, конечно, пуститься в многословные объяснения: это-де мебель, на которой сидят, она имеет четыре ножки, но не имеет спинки и т. д. Можно, кроме того, нарисовать табуретку, приложить к чертежу химический анализ ее материала, таблицу удельного веса разных деталей и еще кучу документов. Все это не помешает. Но лучшим доказательством будет дело. Практика! Сработайте своими руками добротную, прочную, устойчивую табуретку — и любой скептик признает: да, вы до тонкостей знаете ее «внутреннюю сущность». Если кто-нибудь похвастает, что знает, в чем заключается внутренняя сущность тяготения, ради проверки попросите его сделать это самое тяготение без услуг Земли, Луны или Солнца. И, несмотря на то, что тяготение— не табуретка, а нечто более сложное, знающий человек изготовит его моментально. Ему не потребуется для этого ни досок, ни гвоздей, ни клея. Он просто взмахнет рукой. Вот ладонь. На ладони лежит пятачок. Пятачок весит пять граммов. Я резко, с ускорением поднимаю ладонь. Чувствую, что пятачок сильнее на нее надавил. Значит, он стал больше весить. Утверждаю: ускоренным движением ладони я создал добавочное тяготение (это, как видите, гораздо проще, чем сколотить табуретку) . Вы, конечно, возражаете: никакое это не тяготение. Это инерция. Перегрузка — как у взлетающих космонавтов. Пятачок не сразу поддался ускорению — ведь, кроме тяжелой, в нем есть инертная масса. Возражение естественное. Оно полностью согласуется с механикой Ньютона, с первой частью этой книжки и со школьным курсом физики. Но я настаиваю на своем. И прошу вас доказать ваше опровержение не только словами, но и делами. То есть опытом. Очень просто: надо экспериментом отличить инерцию от тяжести. Например, в следующей научно-фантастической ситуации. Черномор-космонавтXXI век. Некая красавица, по имени Людмила, выключает стереоскопический цветной телевизор, поворачивается на правый бок и сладко засыпает в своей малогабаритной квартире на Цветном бульваре. Во время сна ее похищает влюбленный, но без взаимности, космический пришелец Черномор. Осторожно переносит в ракету и улетает прочь с Земли. Допускается, что у Людмилы очень крепкие нервы и она не просыпается от грохота и перегрузок во время старта. Однако через пять-шесть часов она должна-таки проснуться. Черномор этого не хочет, и не без причин. Дело в том, что у Людмилы есть знакомый, по имени Руслан, который служит в Московской радиоастрономической обсерватории. Людмила к нему неравнодушна и даже приняла от него подарок — перстень, в который вделан маленький транзисторный радиопередатчик. Снять радиоперстень с пальца красавицы Черномор не посмел — боялся разбудить. Вот он и опасается, что, проснувшись и узнав о похищении, Людмила воспользуется перстнем, пошлет Руслану сигнал тревоги, и тогда не избежать погони и других осложнений. Ради страховки от таких неприятностей Черномор предпринял широко задуманную мистификацию. Во-первых, пассажирскую кабину ракеты превратил в точное подобие Людмилиной спальни — от трещин в паркете до мастерски декорированного московского дворика за окном. Во-вторых (и это главное!), ракета непрерывно ускорялась вверх. Ускорение было идеально плавным и составляло точно 9,81 метра в секунду за секунду. То есть равнялось g — ускорению свободного падения у земной поверхности- И вот Людмила проснулась. Потянулась, соскочила с постели, попрыгала, мурлыкая песенку про черного кота (она любила старинную музыку), и взглянула на часики с маятником, висевшие на стене. Маятник прилежно качался, стрелки показывали восемь. Людмила вспомнила, что сегодня воскресенье, а значит, не надо бежать на работу. И она юркнула под одеяло... Черномор и на этом строил свой коварный расчет — он знал, что в воскресенье красавица встает около одиннадцати. А ракета мчалась все дальше. Через полчаса она ушла из зоны, подвластной земной администрации. Догадаться о своем незавидном положении Людмиле удалось слишком поздно. Проснувшись около одиннадцати, она накинула халатик и отправилась было в ванну, но обнаружила за дверью комнаты внутреннюю обшивку звездолета, иллюминатор с черным небом и бледного Черномора, робко лепетавшего: Простите меня, Люда, но я не мыслю жизни без вас и вот решился увезти вас в надзвездные края. Наглец! — воскликнула красавица, дала Черномору звонкую пощечину и тут же закричала в свой радиоперстень:— Алло, Руслан! Учти, что меня украли... Напрасно. Земля была уже в ста миллионах километров (можете проверить по формуле Галилея S=gt2/2 а заодно решить, не нужны ли релятивистские формулы) . Руслану пришлось, очевидно, самому гадать, где искать похищенную подругу. Как он это делал — спросите у фантастов. Им, я думаю, подсказана неплохая завязка для романа. Тяготение как ускорениеНам с вами интереснее другое. Опять произошло нечто хоть и удивительное, но более или менее привычное: не удалось отличить движение от покоя. Почему же? Может быть, Людмила не сумела? Будь она физиком и отнесись к делу внимательнее, смогла бы она в закрытой комнате с достоверностью обнаружить равномерно-ускоренное движение и отличить его от земного (в условиях тяжести) покоя? Каким образом, каким прибором, в каком эксперименте? Испробуем механику. Пусть Людмила построит в своей комнате миниатюрную Пизанскую башню и сбросит с нее пушечное ядро и мушкетную пулю. Как они будут падать? С точки зрения ньютоновской физики, они вообще не будут падать. Они полетят равномерно по инерции с той «абсолютной» скоростью, с какой в момент сбрасывания летела ракета Черномора через «абсолютное» пространство. А поскольку ракета летит не равномерно, а с ускорением g, пол комнаты, где находится пленница, очень скоро нагонит ядро и пулю. Если пренебречь сопротивлением воздуха, времени на это понадобится ровно столько, сколько надо для падения ядра и пули с той же высоты под действием земного тяготения. Считая себя неподвижной, Людмила зарегистрирует обыкновенное падение — точно такое же, какое бывает на Земле. А поэтому похищенная красавица не сможет узнать, движется она или пребывает на Земле в неподвижности. Что ж, раз механика не сработала, испробуем оптику. Тут как будто есть надежда на успех, ибо ракета разгоняется (в равномерно и прямолинейно движущейся системе надежды на успех нет, потому что скорость света не зависит от скорости светового источника). Пошлем тонкий луч света параллельно полу, от одной стены комнаты к другой. Пока световые волны пробегут комнату, она, благодаря ускорению вверх, поднимется чуть-чуть больше, чем если бы ускорения не было. Волны же этого ускорения (вверх) не получат—- и поэтому на противоположной стене они окажутся, можно думать, немножечко ниже, чем при равномерном движении или покое. Вот оно, свидетельство ускорения, да? Ничуть не бывало. Луч несет энергию, следовательно, и массу (свет не имеет массы покоя, но имеет массу движения — вспомните предыдущую главу). Масса же обязана притягиваться к Земле. Вот и выходит, что не только в ракете, но и в комнате на Цветном бульваре световой луч отклонится книзу, к полу. В ускоренно поднимающейся комнате — потому, что сам пол, разгоняясь, приблизится к равномерно летящим световым волнам. В неподвижной — потому, что световые волны станут падать под действием силы тяжести — словно пули, выстреленные параллельно горизонту. Наша Людмила (неподвижный относительно комнаты наблюдатель) всякий раз отметит не прямой, а изогнутый путь луча. Свет не помог. Опять невозможно установить движение! Вывод странен: ускоренное движение равноправно с покоем в поле тяготения. Механическим и оптическим экспериментами изнутри системы отсчета не удалось предпочесть одно другому. Этот мысленный эксперимент — начало общей теории относительности. Глава 18. СОМНЕНИЯ И ВОЗРАЖЕНИЯ Жуки-физики в футбольном мячеВот небольшое сомнение. Можно подумать так. Обман Людмилы, предпринятый Черномором, удался благодаря исключительно плавному, строго равномерному ускорению ракеты. Неравномерное ускорение — тряска и толчки — немедленно указало бы, что ракета движется. Удар, встряска — значит, нарушился относительный покой в мчащейся комнате, что тотчас отметят и механические и оптические приборы, да и человеческие ощущения. Верно. Людмилу насторожили бы толчки. Возможно, она догадалась бы, что дело неладно, потому что с детства привыкла к постоянству земного тяготения. Но это отнюдь не подрывает вывода, сделанного Эйнштейном. Ибо привычка к постоянству тяготения — чисто житейская. Нам с вами, не космонавтам, никогда не случалось, сидя на стуле, вдруг почувствовать, что тяжесть стала меньше или больше (во время землетрясений, наверное, ощущение похоже, да еще в лифте, в самолете; но там-то мы наверняка знаем, что движемся). Физик же, заключенный в закрытой ракете, ощутив толчки, должен заглушить в себе голос привычки. Тогда он вправе дать два совершенно противоположных объяснения. Или произошло изменение ускорения. Или толчок вызван изменением силы тяжести. И опять-таки никакими опытами, никакими измерениями он не сумеет отдать предпочтение одному из этих вариантов. Вообразите физическую лабораторию, устроенную внутри футбольного мяча. Крошечные лаборанты (например, какие-нибудь фантастические жуки или муравьи) не знают, что происходит снаружи. То ли мяч скачет по полю под ударами игроков (тогда толчки и перегрузки вызваны ускорениями), то ли мяч неподвижен, но в нем происходит пляска тяготения (тогда толчки вызваны быстро меняющимися силами тяжести). Хладнокровие в лифтеС точки зрения классической механики лаборатория в мяче и ракета Черномора были ареной игры сил инерции. По Ньютону, никаких изменений тяготения там не было. Уместен и обратный пример, в котором ньютонианец нашел бы действие не инерции, а тяжести. Придумал такой пример сам Эйнштейн. Это падающий лифт. Оборвался канат, кабинка лифта стремглав падает, влекомая земным тяготением. В конце концов она достигает дна шахты — и наступают печальные последствия. Если вы достаточно хладнокровны, чтобы размышлять на научные темы в падающем лифте, то можете, по Эйнштейну, считать себя неподвижным. Это засвидетельствуют и механические и оптические опыты. Они зарегистрируют идеальную невесомость и строго прямолинейное распространение светового луча — как в далеком космосе, в ракете, которая летит без ускорений, по инерции. Или по инерции же пребывает в покое (что, конечно, изнутри неотличимо от прямолинейного равномерного движения). Прежде инерция была сведена к тяготению. Ускорением мы создали тяжесть. Теперь же, наоборот, тяготение сведено к инерции. Ускорение ликвидировало тяжесть. Итак, Эйнштейн считает равноправными две системы отсчета: ракету, неподвижную в поле земного тяготения, и ракету, летящую вне поля тяготения с ускорением g. Либо лифт, покоящийся или равномерно летящий в глубинах космоса вне полей тяготения, и лифт, который свободно падает в поле тяжести. Основание для такого заключения дал высший судья физических высказываний — его величество эксперимент. Если никакими способами невозможно отличить одно явление от другого, значит, эти явления физически тождественны. Их различие — только в названии. Немец говорит «der Tisch», русский — «стол», а предмет, обозначаемый этими названиями, один и тот же, ибо физических признаков отличия нет. Похищенная Людмила, веря в свою неподвижность, назвала стремление тел книзу тяготением. Руслан, от которого умчали Людмилу, сказал бы: «Нет, это инерция». Обитатель падающего лифта, считавший себя неподвижным, не находил никакого тяготения и объяснял этим свою невесомость. Для него лифт летел по инерции. Лифтер же, оставшийся снаружи, объяснил движение лифта, как и пропажу в нем веса, тяготением. Разные наблюдатели — разные слова. А суть — одна. Инерция и тяготение — по Эйнштейну, физически тождественные явления природы (правда, с оговоркой, которую я приведу в следующей главе). Таков неожиданный и парадоксальный принцип эквивалентности инерции и тяготения. Он был провозглашен Эйнштейном еще до опубликования общей теории, в 1913 году. А из него прежде всего следует вывод, к которому мы добирались через всю книжку: инертная масса и тяжелая масса равны не потому, что они совпадают случайно (так выходило по Ньютону, помните?), а потому, что это одна и та же масса. Просто масса. Стадионы на ракетахНе очень вразумительные разговоры о табуретке, пятачке и изготовлении тяготения без услуг земного шара (хотя бы для организации в космосе Олимпиады № 100) теперь находят обоснование. Что ж, резко подняв ладонь с пятачком, я действительно сотворил тяготение. Для физика-лилипута, пребывающего, допустим, на моей ладони, пятачок стал тяжелее — это покажут любые весы. А принцип эквивалентности стоит на страже справедливости такого мнения. Тот же принцип поможет избежать противоречий среди участников сотых Олимпийских игр. Для спортсменов разных планет придется устроить в космосе по- разному ускоряющиеся крытые стадионы в виде платформ с колпаками, удерживающими искусственную атмосферу. Для спортсменов-землян потребуется стадион, разгоняемый ракетами «вверх» с ускорением g, для селенитов—другой, разгоняющийся с ускорением g/6, и т. д. На всех стадионах будут разные силы тяжести — по заказу судейской коллегии. И — никаких планет! Никаких «спокойных» источников тяготения вроде Земли! Стадионы летают взад-вперед (повороты во время перерывов), и всюду спортсмены прыгают, бегают, метают диски, гоняют и бросают мячи — в условиях привычной тяжести, как у себя на родине. Тяготение не имитируется, не подделывается. Оно создается. Правда, правнуки-олимпийцы могут возразить, что проект технически сложен: требуется множество ракетных двигателей, возникают хлопоты с организацией движения стадионов. Предвидятся протесты и со стороны правнуков-болельщиков. Им, видите ли, неудобно будет летать без конца со стадиона на стадион и никак не удастся обозревать собственными глазами сразу полную картину состязаний (телевизоры к тому времени, надо думать, всем надоедят). Хорошо. В таком случае я предлагаю другой — упрощенный проект. Он свободен от перечисленных недостатков, но, правда, имеет некоторые другие. Пусть он называется олимпийской каруселью.  Олимпийская карусель Олимпийская карусель Когда я в городском саду катаюсь на карусели, меня тянет вбок по радиусу центробежная сила инерции, но лодка моя прикреплена к спице, а спица надета на ось. И я не могу улететь вбок, движусь по кругу, удерживаемый центростремительной силой связи с осью. А инерцию воспринимаю как тяжесть, влекущую меня вбок, прочь от оси. С точки зрения кассира, который продает билеты, это, правда, не тяжесть, а все-таки инерция, что, однако, по Эйнштейну, не меняет сути явления. Так в обычной карусели. Так и в олимпийской. Она должна быть достаточно велика, эта космическая карусель. Вместо карусельной лодки или лошадки на ее спице — все тот же крытый стадион. Плоскостью своего поля он поставлен перпендикулярно к спице и параллельно оси вращения. Под прозрачным куполом — воздух. Таким образом, «верх» стадиона обращен внутрь, к оси карусели. Чем сильнее надо сделать тяготение, тем быстрее придется вращать спицу и тем дальше от оси расположить стадион. Расстояние от оси лучше делать побольше. И вот почему. Пусть длина спицы, на которой держится стадион, невелика — скажем, 100 метров. Тогда поле стадиона (шириной в те же 100 метров) будет либо кривым, как дно корыта, либо, если его сделать прямым, в разных местах будет иметь разное тяготение. В центре прямого поля тяготение окажется в v3/2 раза меньше, чем по краям (учтя, что центробежная сила пропорциональна радиусу, проверьте это сами — простейшая геометрическая задачка). В обоих случаях прыгать и бегать будет затруднительно. Спортсмены попросят устроить прямое поле. И чтобы везде на нем было одинаковое тяготение. Исполнить это требование можно. Надо сделать так, чтобы размер стадиона был невелик по сравнению с длиной спицы. А поскольку длину беговых дорожек наши потомки, надо полагать, менять не пожелают, придется увеличить длину спицы. При двух-трехкилометровой спице на прямом стадионе вес игроков, перебегавших с краев к центру, будет варьироваться меньше, чем на свою тысячную долю. Пожалуй, терпимо. А какова должна быть скорость вращения космической олимпийской карусели? Чтобы устроить на стадионе, закрепленном на спице в километре от оси, такое же по силе тяготение, как на земной поверхности, стадион придется (опять простенькая школьная задачка!) заставить совершить один полный оборот вокруг оси за две минуты. Линейная скорость стадиона при этом окажется довольно значительной — 100 метров в секунду[13]. Говорит Маленький ПринцВ чем достоинства олимпийской карусели? Ее не придется непрерывно разгонять, как того требовали ускоряющиеся платформы со стадионами. В космосе отсутствует сопротивление среды — значит, достаточно одного хорошо рассчитанного толчка ракетными двигателями, и карусель начнет кружиться как положено и создавать надлежащее тяготение. В общем, проект вышел неплохой. Я даже намеревался взять на него патент и принялся сочинять авторскую заявку. Но произошло волшебство: на мой письменный стол прилетел Маленький Принц из сказки Антуана де Сент-Экзюпери. Он сказал: Здравствуй, — и присел на стопку книг. Здравствуй, — сказал я.— Как поживаешь? Он не ответил, поглощенный разглядыванием того, как я выписываю буковки на белой бумаге. Чтобы не вспугнуть его, я сделал вид, что нисколько не удивился. Наконец он вежливо попросил: Пожалуйста, нарисуй мне то, что ты описываешь. Я нарисовал ему олимпийскую карусель с беговой дорожкой и объяснил, что к чему. Маленький Принц на минутку задумался, и славное личико его стало печальным. Губы вздрогнули, из глаз полились слезы. Я опешил. И тут же заговорил наигранно-бодрым голосом: Ты совершенно напрасно плачешь. С чего это вдруг? Или тебе не нравится мой проект? Не нравится.— Маленький Принц проглотил рыдание. Почему же? Взгляни-ка, какой он хороший! Каждый житель Солнечной системы получит на нем свою силу тяжести... Да, каждый, — сказал обиженно Маленький Принц.— Каждый, кроме меня... Почему же? Потому что я хочу выпуклый стадион. И выпуклую беговую дорожку. Да такую, чтобы всюду тяжесть была направлена к центру кривизны. Как на моем астероиде. А ты можешь сделать только прямой или вогнутый... Маленький Принц снова заплакал. Он говорил, что не желает бегать на столе. Он ведь прилетел с крошечной планеты, где любая спортивная площадка как корка на куске арбуза. Я огорченно слушал и не знал, чем его утешить. Действительно, в моих проектах никак нельзя было устроить то, что подошло бы моему новому заказчику.  Карты спутаны Карты спутаны Надеюсь, после визита Маленького Принца читатель несколько запутался. Это как раз и требуется для четкого понимания дальнейшего. В самом деле, вышло что-то нескладно. С одной стороны, приведены факты, доказывающие полную взаимозаменяемость инерции и тяготения: похищенная Людмила, жуки-физики в мяче, хладнокровный человек в падающем лифте дружно засвидетельствовали невозможность отличить одно от другого. На этом основании был провозглашен эйнштейновский принцип эквивалентности инерции и тяготения, утверждена относительность всех движений (а не только равномерных и прямолинейных). Стало понятно равенство тяжелой и инертной масс, разъяснялось как будто загадочное свойство пушинки и камня падать в пустоте одинаково быстро. Сведя тяготение к инерции, я так обрадовался, что взялся выдумывать способы технического изготовления разнообразных сил тяжести для спортивных целей. Предложил ускоряющиеся платформы-стадионы. Изобрел космическую олимпийскую карусель. Все шло ловко и гладко. Но тут явился Маленький Принц и смешал карты. Как это произошло? Маленький Принц напомнил нечто очень важное: центральность сил тяготения. Земля притягивает к себе тела так, как если бы вся ее масса была сосредоточена в одной точке — в центре масс. И Солнце, и Луна, и любая планета, любая звезда. Потому-то и получился на планете Маленького Принца выпуклый стадион со строго одинаковым тяготением в разных точках. Да и на больших планетах, если уж быть пунктуально точным, стадионы со всюду равной тяжестью теоретически чуть- чуть выпуклы. Однако никаким ускоренным движением невозможно создать в жесткой системе отсчета инерцию, обладающую этим же свойством. Как ни хитри, этого не добьешься. Инерцией можно разбросать тела в разные стороны по расходящимся линиям (на карусели), можно заставить их лететь или давить в параллельных направлениях (на ускоряющихся платформах). Можно устраивать вогнутые и прямые стадионы — пожалуйста, сколько угодно. Но устремить инерционное давление по линиям, сходящимся к какому-то центру, нельзя. Ведь для создания центростремительного тяготения жесткая система отсчета должна сразу ускоряться и «вперед», и «назад», и «вверх», и «вниз», и как угодно «вбок». Она должна вести себя по примеру ускоренно раздувающегося шара. Тела на таком стремительно растущем шаре станут не только давить «вниз», к центру, но и разбегаться в стороны. Но тогда он потеряет свою жесткость, разрушится, взорвется. Между тем предметы на земной поверхности в стороны не разбегаются, Америка и Азия не рвутся в небеса, не разгоняются в противоположных направлениях. Нет инерции, в точности повторяющей земное тяготение, — сразу все и надолго (раздувающийся ускоренно шар, правда, воспроизведет полное тяготение, существующее у земной поверхности, но лишь на бесконечно короткое время — пока его стремительно растущий радиус проскочит через величину, равную радиусу Земли). Нет, значит, и инерции, которая ликвидировала бы земное тяготение — сразу все и надолго (падающий лифт, в котором пропадет все земное тяготение, должен охватывать планету и ускоренно лететь к ее центру, непрерывно сокращаясь в размерах, что не может, конечно, продлиться достаточно долго). По этой причине буквально все наши примеры выглядят не вполне верными. Та же Людмила, установи она безупречную параллельность отвесных линий, могла с уверенностью решить: я не на Земле. Потому что на Земле отвесные линии сходятся к центру планеты. Угол между ними не равен нулю. Подобные измерения могли в принципе сделать и жуки-физики в мяче. А хладнокровный обитатель падающего лифта мог заметить странное поведение двух невесомых грузов, «неподвижно» парящих возле противоположных стенок кабины. По мере приближения лифта к центру Земли эти грузы сближались бы. У самого центра они стукнулись бы друг о друга. Словом, Маленький Принц поставил под сомнение столь заманчивую, столь восхитившую нас эквивалентность инерции и тяжести? Доказал, что тяготение, благодаря его центральности, нельзя свести к инерции? И да и нет. От малого—к большомуРазумеется, Эйнштейн великолепно понимал возражения типа тех, что у нас прозвучали из уст Маленького Принца. Он понимал: выпуклый стадион с помощью инерции не устроишь. Сразу все, везде и надолго земное тяготение не устранишь падением. Он знал, что, вообще говоря, инерция и тяготение в старой, традиционной физике в любых масштабах не эквивалентны. И все- таки он провозгласил принцип эквивалентности! Почему же? На каком основании? И для чего? Отвечу сразу: ради создания новой физики, более общей и точной, чем прежняя. Основания: все описанные выше мысленные и действительные опыты плюс оговорка, которую я раньше не приводил, ибо только теперь будет понятна ее важность. Оговорка такая: принцип эквивалентности инерции и тяготения справедлив для местных, или, по выражению Эйнштейна, локальных явлений. Людмила в своей комнате на Цветном бульваре — явление сугубо местное. То, что где-то очень далеко, в шести тысячах километров над ней, есть центр тяжести планеты, не играло роли. Непараллельность отвесных линий зафиксировать опытом, может быть, и удастся (если эти линии отстоят в Людмилиной комнате на метр друг от друга, то угол между ними составит десятимиллионную долю угловой минуты), но поправка эта не изменит качества явления. В структурах полей сил инерции и тяготения обнаруживается чисто математическое различие, которое никак не сказывается на физической сущности и действии возникающих сил. Локальное явление — и падающий лифт, если его ширина нормальна (не шире Черного моря), шахта хоть и глубока, но не пронизывает насквозь планету, и время падения не слишком велико. В обычном лифте, если он падает, тяжесть пропадает полностью. Принцип эквивалентности безусловно исполняется. Даже крохотная планетка Маленького Принца (если она реальная, не сказочная) обязана создавать тяготение, строго согласное с принципом эквивалентности в достаточно малых, локальных масштабах. Малюсенький стадиончик (для футболистов-микробов) и на такой планетке будет иметь почти плоскую поверхность, а не выпуклую. И его удастся в точности повторить, если воспользоваться услугами сил инерции. Так всюду. Любое тяготение, несмотря на свою центральность, в локальных явлениях, в малых масштабах или коротких промежутках времени неотличимо от инерции. Соответствующую «малость» всегда можно подобрать, она совсем не обязательно ничтожна, она может быть и весьма крупной. Этот факт универсален. Исключений нет. Следовательно, принцип локальной эквивалентности инерции и тяготения не должен вызывать возражений у физиков. А это открывает великолепные возможности для исследований. Вот что надо выяснить. Раз силы инерции и тяжесть едины в малом, то как они соотносятся в большом? Не вносит ли это какой- либо новой, неведомой ранее ученым, черты в физику нашего мира? Искать ответы — значит погрузиться в дебри общей теории относительности. Что мы сейчас, набравшись храбрости, и сделаем. Вооружимся терпимостью к варварским упрощениям и постараемся постичь хотя бы самую суть этой труднейшей теории. Глава 19. НА ВРАЩАЮЩЕМСЯ СТАДИОНЕ Путевка в XXIII векЛюбой современный читатель этой книжки, даже семидесятилетний старец (если таковой среди читателей найдется), может, в принципе, поспеть на сотую Олимпиаду, которая состоится, как я уже говорил, летом 2292 года. Для этого не нужно погружаться в анабиоз, обретать бессмертие или фантастическое долголетие. Нужно только совершить некое путешествие. О том, что подобное теоретически возможно, помнит, вероятно, каждый, кто читал одиннадцатую главу. Через несколько страниц я обещаю вернуться к этой теме. А пока прошу вас вообразить себя счастливцем, заполучившим туристскую путевку на сотую Олимпиаду. Итак, прозвучали фанфары, взлетели флаги. В открытом космосе вдали от планет вертится космическая карусель: один стадион на спице с противовесом кружит вокруг оси. Туристов, конечно, много, места для них мало, поэтому вся конструкция использована под трибуны. Скамейки всюду — и вокруг стадиона, и на спице, и на оси. Теперь внимание. Вы — болельщик. Сидите на скамье трибуны, которая укреплена на спице у самой оси. И кружите вокруг оси вместе со спицей. Вам не очень удобно. Тяжести почти нет — вы ведь рядом с осью, и центробежная сила мала, ибо она зависит от радиуса вращения, а радиус этот для вас невелик. Далеко «под вами» прикреплен к той же оси олимпийский стадион, и вы смотрите на него в бинокль (или даже в телескоп). Разумеется, вам хочется «вниз», на стадион — в привычную тяжесть, к полю. Но все близкие места заняты, и вам поневоле приходится обозревать игры издалека, с птичьего полета. Еще одно (приятное) известие. Наш старый знакомый Клио, бывший космический пират, исправился, остепенился, обзавелся многочисленным семейством и тоже явился на Олимпиаду. Он работает тут на должности механика, следит за исправным вращением стадиона и строгой неподвижностью оси. (Если ось будет шататься, на стадионе нарушится постоянство центробежной силы, создающей тяжесть, и состязания пойдут насмарку). Очень ответственное дело у старого Клио! Оно осложнено тем, что сооружение ни на чем не укреплено — витает в межпланетном пространстве. Рабочее место Клио — на оси. А вы — на спице около оси. Поэтому он может переговариваться с вами, сверять часы, делиться впечатлениями. В этой своеобразной обстановке вам и предстоит познакомиться с любопытными особенностями общей теории относительности. Рекорд под вопросомНа стадионе — состязания спринтеров-землян. Судьи отметили рулеткой стометровку, сверили свои сверхточные секундомеры (все измерительные приспособления были заранее сравнены с эталонами из Всемирной палаты мер и весов). И вот — выстрел, старт, щелчки секундомеров. Рванулась восьмерка бегунов. И спустя несколько секунд — бурный финиш. Судьи на стадионе единодушно фиксируют победу человекоподобного робота Клиотти. Это — внук Клио! Чемпион пробежал стометровку за семь и две миллионных секунды. Абсолютный мировой рекорд! Прежний рекорд, установленный на Земле, был чуть-чуть хуже. На стадионе ликование. Победителя обнимают, качают. Однако некоторые болельщики, наблюдавшие забег издалека, с трибун у оси космической карусели, не согласны с оценкой судей. По их мнению, соревнование проведено неверно. Во-первых, дистанция бега отмечена с ошибкой — на ничтожную долю миллиметра короче ста метров. Во-вторых, время, за которое Клиотти пробежал дистанцию, на столь же крошечную часть секунды больше, чем заявили судьи. А раз так, то никакого абсолютного мирового рекорда нет. Клиотти, хоть и победил, но не вышел в абсолютные чемпионы. Надо сказать, что болельщики, сидящие у оси, сделали свои оценки отнюдь не на глазок. Они располагали точнейшими угломерными инструментами, идеальными сверхсекундомерами. Вы, сидя рядом с ними, тщательно проверяли их измерения. Клио, находясь на оси, тоже проверял и сам все измерял. Точность оценок, таким образом, была гарантирована. С другой стороны, на стадионе измерения тоже были исполнены безукоризненно. И вот шум, волнения. Болельщики с оси кричат: — Эй вы, там, внизу! Сапожники! На мыло!.. Судьи хранят олимпийское спокойствие, но постаревший и поумневший Клио, обрадованный победой внука-чемпиона, возмущен: — Самих вас на мыло! Не знаете теории относительности!.. И на этот раз Клио прав. Болельщики у оси напрасно нервничают. Несмотря на справедливость своих оценок, они зря обвиняют судей в ошибках. Никаких ошибок нет, рекорд установлен по всем правилам. А спор возник по прежней, уже традиционной для этой книжки, причине: не учтены особенности системы отсчета. Реабилитация спринтераПри проектировании космической карусели обсуждались, быть может, два варианта ее конструкции. В первом предлагалось спицу жестко скрепить с осью (как в колесной паре железнодорожного вагона), чтобы ось вращалась вместе со спицей. Это удобно и просто. Однако по непонятным причинам был принят второй, менее удачный вариант — спица надета на ось свободно и кружит вокруг нее в подшипнике (вроде велосипедного колеса). Так и сделали карусель. И, запуская ее, ось установили неподвижной относительно звезд. (Как это устроили, я не знаю, но, допустим, устроили.) Спица стала двигаться относительно оси и, следовательно, относительно звезд. Благодаря такой конструкции карусели Клио (тому, кто сидит на неподвижной оси) особенно ясна причина разногласий в оценке забега Клиотти. Ведь ось неподвижна, а стадион относительно нее движется. В любой достаточно малый отрезок времени можно считать, что стадион движется относительно оси равномерно и прямолинейно. Значит, Клио может вспомнить частную теорию относительности и учесть релятивистские эффекты. По его отсчету продольные (перпендикулярные к спице) длины стадиона будут короче, секунды же стадиона — дольше. Соответственно, дистанция забега Клиотти короче, длительность забега больше, чем для него самого и для окружающих его бдительных и пунктуальных судей. К такого рода поправкам мы, кажется, уже привыкли с одиннадцатой главы. Значит, для Клио разница в длинах и длительностях стадиона ясна. Поэтому он знает, что в собственном времени и расстоянии стадиона Клиотти поставил-таки рекорд. Судьи правы. Но как объяснить это вам и болельщикам, сидящим на спице? Вы ведь неподвижны относительно стадиона. Стадион и вы покоитесь в одной и той же жесткой системе отсчета. И тем не менее и вы и болельщики отметили те же самые изменения стадионного времени и стадионной длины, что и движущийся относительно стадиона Клио. Почему? Именно потому, что вертится космическая карусель. Именно потому, что движение стадиона не прямолинейное. Публика, сидящая на спице рядом с осью, в каждый момент времени имеет меньшую скорость относительно оси, чем обитатели стадиона, укрепленного на самом конце спицы. Это понятно всем, кто хоть раз в жизни вертел пращу или закидывал удочку: конец лески с грузилом и крючком движется быстрее, чем ее начало, привязанное к удилищу. А раз ваша скорость относительно оси мала, то и релятивистские эффекты относительно оси ничтожны. Во всяком случае, приближаясь по спице к оси, вы можете свести их на нет. Вот резко утрированный пример. Стадион на 300-километровой спице делает 30 оборотов в секунду. Тогда он мчится относительно оси со скоростью 100 тысяч километров в секунду. Треть скорости света! Релятивистские эффекты стадиона с оси вполне заметны. А зритель, сидящий на спице в метре от оси, плетется относительно оси всего лишь со скоростью звука. И никаких релятивистских эффектов практически нет. Словом, раз уж вы — болельщик, сидящий на спице у оси, то у вас метры такие же, как у Клио, и ваши секунды такие же, как у Клио. А поэтому ваша точка зрения и точка зрения Клио на метры и секунды стадиона практически совпадают. Если для него стадионные сантиметры укорачиваются, значит, и для вас тоже, если для него стадионные секунды удлиняются, значит, и для вас тоже. Шаг через векаСведениями, добытыми на сотой Олимпиаде, я воспользуюсь, чтобы выполнить обещание, данное в начале этой главы, — объясню, каким способом вы, человек XX века, не старясь, попали на Олимпийские игры в XXIII век. Теоретически (и фантастически) для обгона столетий годится устройство, называемое центробежной машиной времени. Войдя в нее, погружаешься в замедленное время: сутки в машине равны году или столетию вне ее. Степень замедления зависит от настройки. На пульте машины есть регулировочная ручка. Оператор ставит ее на цифру «2» — время внутри машины течет вдвое медленнее, чем снаружи. Поставил ручку на «1000» — время в машине замедлено в 1000 раз. Удобно и практично. Кроме того, на пульте размещены всевозможные экраны, кнопки, телефоны. Есть еще люки для передачи пищи тем, кто находится внутри. Пользоваться этими люками придется не часто: при времени, замедленном в тысячу раз, обитатель машины будет обедать раз в три года (это, разумеется, наши, внешние три года, которые для него, сидящего в машине, составят одни сутки). Ну, снаружи мы машину оборудовали. А внутри она устроена еще проще. Ничего таинственного и нового. Открываем двери. Входим. Видим внутри карусель. Да-да, опять карусель, но маленькая, сказочно сверхпрочная, способная крутиться с гигантским числом оборотов (что-нибудь порядка десятка миллионов в секунду). Или, если хотите, центрифуга — наподобие той, в которой тренируют космонавтов, только неизмеримо более быстрая. Ручка регулировки темпа времени соединена с редуктором — чем быстрее вращение карусели, тем медленнее в ней течет время. Действие машины понятно всем, кто внимательно прочитал предыдущие страницы. Время в ней тормозится по той же причине, по какой оно тормозилось, с точки зрения болельщиков у оси, на стадионе космической карусели. Вот и весь секрет. Недавно физики устроили лабораторную модель центробежной машины времени — попросту вращающийся диск, вроде проигрывателя. И сумели зафиксировать растяжение секунд на движущемся крае диска. Получено подтверждение эйнштейновского предсказания даже при вращении со скоростью долгоиграющей пластинки. Каждая секунда края стала дольше секунды центра на миллионные доли от одной миллиардной доли. Как проводятся столь тонкие опыты, я расскажу потом. А пока немножко огорчу вас: человеку путешествовать в будущее в таких машинах, к сожалению, не удастся. И вот почему. Свежее желеЗаметное растяжение времени требует колоссальных оборотов центрифуги, а значит, гигантских центробежных сил, которые мгновенно превратят машину в пыль, а путешественника — в мокрое место. В одном шутливом фантастическом рассказе приведен именно этот трагический случай: некий ученый, пожелавший самолично испытать сверхпрочную центробежную машину времени, был извлечен из нее в виде желе. Все-таки испытание прошло небезуспешно: было доказано, что время в машине действительно замедлилось— от внешнего года до двух внутренних суток. Потому что выгруженное из машины желе оказалось абсолютно свежим. Этот печальный исход ставит крест на центробежной машине времени как средстве человеческого путешествия в завтрашний день. Однако он не отвергает других способов прыжка в будущее. Наиболее безопасен сверхбыстрый космический полет с возвратом к месту старта. Вспомните космонавток Аллу и Эллу из одиннадцатой главы. Они мчались друг относительно друга прямолинейно и равномерно, и для каждой другая старела медленнее. Но когда одна из космонавток (допустим, Алла) повернула ракету назад и догнала улетевшую подругу, именно вернувшаяся космонавтка оказалась моложе. Этому факту теперь можно дать новое объяснение: Алла совершила путешествие, подобное движению стадиона в космической карусели или желе в центробежной машине времени. А Элла, продолжавшая прямое движение, была в роли оператора машины или болельщика у оси космической карусели. Благодаря гигантской относительной скорости полета время для Аллы замедлится очень заметно. Алла может оказаться моложе Эллы на год, на десять лет, на миллион лет и при этом останется жива и здорова. Подсчитано, например, что космонавт, вылетевший с Земли и пролетавший 40 лет (своих) с вполне терпимым ускорением 2g, вернется на Землю через 10 000 земных лет! Правда, для подобного полета требуются неправдоподобные запасы топлива, но аналогичное путешествие на дистанцию в 300 лет выглядит более или менее допустимой фантазией. А значит, вы, дорогой читатель, как раз таким способом и прилетели в 2292 год на сотую Олимпиаду. Между тем там разворачиваются весьма любопытные события. Нам пора туда вернуться. Глава 20. СЮРПРИЗЫ ИНЕРЦИИ Когда погасли звездыПотеряв надежду растолковать болельщикам релятивистские эффекты, механик Клио уходит с трибун, чтобы смазать ось олимпийской карусели. Кряхтя, тащит из кладовой канистру смазочного масла, выливает его в огромный подшипник. Дело это трудоемкое. Клио устает, садится на пустую канистру и задумывается. Ему приходит в голову здравая идея — а зачем, собственно говоря, нужен этот подшипник? Разве нельзя обойтись без него? Это не помешает и смотреть игры и делать дистанционные оценки. Неважно ведь, сидит наблюдатель на оси или на спице рядом с осью — все равно события на стадионе воспринимаются им одинаково. Но тогда совсем не обязательно, чтобы спица двигалась относительно оси. Можно намертво закрепить ее. И не придется заботиться о подшипниках. Сказано — сделано. Спица спаяна с осью (для этого Клио, по обыкновению, применил свое огненное дыхание). Получился «железнодорожный» вариант карусели — более простой и удобный, тот, что резонно было устроить с самого начала. В этой спокойной обстановке, располагающей к отдыху, Клио устраивается в кресле, вытягивает ноги... Но вдруг, ради удобств популяризации, наступает очередное маловероятное событие — гаснут звезды. Да-да, гаснут все звезды на небе. Наплыло облако космической пыли или что-нибудь в этом роде. Это не очень-то приятно для механика. Это сбивает его с толку. Кругом кромешная тьма, не видно ни зги. Пропало ощущение плавного вращения, которое только что создавалось поворотом сверкающей небесной сферы. Вместо вращения Клио чудится полный покой, незыблемая неподвижность. Он ведь скрепил ось со спицей, относительное движение их в подшипнике прекратилось, и к тому же исчезло перемещение небесных ориентиров — звезд. Словом, пропали внешние признаки, по которым можно доказать собственное движение. И вот Клио приходит в голову тревожная мысль: а что, если и в самом деле карусель остановилась? Завязла в этом космическом облаке и потеряла вращение? Он, механик, должен быть готов к любым неожиданностям. «Нет, — думает Клио, — этого не может быть. Случись такое — исчезла бы центробежная сила на стадионе, бегуны там стали бы невесомы и не смогли бы бегать». А игры, как он видит, идут своим чередом. Соревнования продолжаются. В ярком свете прожекторов спортсмены вообще не замечают нагрянувшей небесной темноты. Им не до звезд. Значит, невесомости на стадионе нет, все, видимо, в порядке. Тем не менее Клио гложет червь сомнения. Возникает совсем уж неправдоподобное предположение: остановилась карусель, быть может, потому, что стадион притянулся к какой-нибудь планетке, к тяготеющей массе, и она создала «настоящую» тяжесть, подобную той, которая была сфабрикована вращением — центробежной силой инерции. Что и говорить, событие довольно нелепое. Но в этой досадной тьме Клио ничем не может доказать неверность изложенной гипотезы. А если что-то подобное случилось, он это обязан знать — такая уж у него должность. Как же быть? Неужели нет никакой возможности узнать, движется стадион или покоится в поле тяготения? Эти вопросы Клио задает вам, читателю и гостю сотой Олимпиады. Если верить эйнштейновскому принципу эквивалентности, задача безнадежна, — отвечаете вы.— Никаких признаков отличия существовать не должно. Вот оказия! — говорит Клио.— А может, его как-нибудь обойти, этот принцип?.. Наказание за кощунствоРастерянный и обескураженный, Клио старается вывернуться из затруднительного положения. И в конце концов, как ему кажется, находит одну хитрость. «Те самые различия в отсчетах расстояния и времени, которые так разволновали публику на трибунах, — вот, — думает робот-механик, — признак вращения карусели». Ведь, как говорилось выше, это релятивистские эффекты, и вызваны они именно движением стадиона. Так ведь? Объяснение кажется Клио убедительным и утешительным, потому что неучи-болельщики продолжают кричать и возмущаться (доносятся возгласы «Долой жуликов!», «Судьи подыгрывают землянам!»). Значит, и сейчас, во время новых забегов на стадионе, релятивистские эффекты налицо и, следовательно, стадион движется, карусель вращается. Чем не доказательство?![14] Клио доволен. Он восхищен своей сообразительностью. И успокоен, уверен, что в наплывшей темноте с каруселью ничего не произошло. В пылу самодовольства он забывает, что допустил непозволительную вольность— кощунственно пренебрег эйнштейновским принципом эквивалентности инерции и тяготения. Не мудрено, что хвастливое ликование длится недолго. Облако космической пыли исчезает, снова зажигаются звезды — и Клио, к своему ужасу, видит: они неподвижны! Карусель остановилась. И под стадионом торчит, как он и боялся, неведомо откуда взявшаяся злосчастная планетка, маленькая, да удаленькая — сверхплотная и создавшая поэтому достаточное тяготение на стадионе. И, следовательно, именно это «настоящее» тяготение вызвало на стадионе замедление времени и уменьшение расстояний. Так же, как раньше эти эффекты вызывало вращение карусели. Как видите, принцип эквивалентности опять оказался справедливым — в масштабах стадиона поле сил инерции, вплоть до тончайших своих особенностей, повторено гравитационным полем. Не сумел хитрый Клио обойти Эйнштейна. Не сумел отличить вращение от покоя в условиях тяжести. А все потому, что сей эпизодический персонаж, во- первых, остался личностью, склонной к нечестным манипуляциям, а во-вторых, знает теорию относительности только до того места этой книжки, в котором он очередной раз появляется. Две моралиПринимаю как должное упреки в чрезмерной фантастичности и искусственности вышеизложенного мысленного эксперимента. Но зато из него следуют поучительные морали, с которыми, как мне кажется, теперь будет легко согласиться. Первая мораль. Не только скорости, но и ускорения ведут к изменениям времени и пространства в движущихся системах отсчета (с точки зрения наблюдателей, движущихся иначе). Такова лодка вращающейся карусели. Центростремительная сила все время ее сворачивает с прямого пути, отчего появляется центробежная сила инерции. Поэтому можно сказать короче: в поле инерционных сил происходит изменение времени и пространства. Любопытно, что это следует только из частной теории относительности, которая, вообще говоря, применима лишь к системам отсчета, движущимся прямолинейно. Тем не менее вывод строг, его много раз приводил сам Эйнштейн. И вторая мораль. Если инерция изменяет время и пространство, то, не желая повторять ошибки злополучного Клио, мы смело применяем принцип эквивалентности и сразу заключаем: тяготение тоже обязано изменять время и пространство. Раз, по принципу эквивалентности, сила инерции в локальных масштабах неотличима от тяжести, это должно касаться всех и всяческих проявлений инерционных и гравитационных сил. Тут уже действует общая теория относительности. Конечно, у Эйнштейна на пути к этому удивительному заключению не было никаких спортивных и космических небылиц. Была строгая логика — сухая, трудная и, быть может, скучная для людей, мало склонных к предельно абстрактному мышлению. Было обобщение идей частной теории, соединение их с принципом эквивалентности, и в итоге родилось предсказание: в гравитационном поле время и пространство деформированы. От локального к всеобщемуВ поворотных местах популяризаторского сюжета этой книжки я следую доброй пословице: «Повторенье — мать ученья». На этом основании вкратце вспомним логическую цепочку предыдущих глав. В малых масштабах подмечена неразличимость инерции и тяжести (Людмила, обманутая Черномором, и т. д.). Отсюда провозглашен принцип эквивалентности инерции и тяготения. Далее выяснено, что в поле сил инерции происходит деформация времени и пространства (споры болельщиков на сотой Олимпиаде). По принципу эквивалентности последовал вывод: в поле тяжести тоже происходит деформация времени и пространства (казус с механиком Клио). Так сделан немаловажный шаг — отыскан физический признак, присущий в равной мере силам инерции и тяготению: тут и там для внешнего наблюдателя неизбежно изменение времени и пространства. Пока это заключение законно только в локальных масштабах, где безоговорочно справедлив принцип эквивалентности, то есть для ограниченных объемов или малых промежутков времени (вспомните возражение Маленького Принца). Для планеты в целом такой вывод сделать нельзя, потому что Земля имеет центр масс. Полное земное тяготение, благодаря его центральности, сразу везде и надолго невозможно повторить неинерциальным движением или, наоборот, уничтожить его свободным падением системы. Вышеизложенное известно из предыдущих глав. А вот новое. Выдвигается гипотеза: раз в локальных, местных явлениях тяготение, сведенное к инерции, изменяет пространство и время, то и в крупных масштабах, где сведение невозможно, должна тем не менее происходить какая-то деформация пространства и времени. Гипотеза эта напрашивается сама собой. Ведь полное тяготение Земли складывается из сил тяготения, исходящих от ее маленьких частей. В каждой части пространство и время изменяются, значит, и во всех частях вместе — тоже. Из сугубо локальных явлений извлечено, таким образом, заключение совершенно универсальное: наша планета всей своей массой деформирует пространство и время. И Солнце, и любая звезда, и любая галактика. Всякая масса вещества обязана обладать поразительной способностью — способностью искривлять мир. Что же это такое — искривлять мир? Дабы легче постичь это, еще раз сосредоточьтесь и следующие три главы прочтите с усиленным вниманием. Глава 21. ВДОЛЬ ПОВЕРХНОСТИ Кривые дроваГеометрия — самая древняя в обширной семье математических наук. И чуть ли не самая мудрая. Учителя единодушно признают ее лучшим пробным камнем математических способностей — она очень глубока по мысли, изящна, безупречно стройна. Юный Эйнштейн, когда ему в руки попалась тоненькая геометрическая книжечка, был восхищенно удивлен открывшимся волшебством логического творчества: шаг за шагом из простейших постулатов вырастала гармония лемм и теорем, все более запутанных, тонких, подчас неожиданных. Великий физик назвал эту книжечку в числе отправных пунктов своего марафонского бега от удивлений. Да, геометрия достойна высших похвал. Может быть, даже поэм и од. Жаль, что их, кажется, еще не успели сочинить. Зато на геометрические темы придумано порядочно поговорок и пословиц. Есть даже анекдоты. Мне почему-то страшно нравится тот, где некий машинист на паровозе кричит кочегару: — Эй, кочегар, кидай в топку кривые дрова! Въезжаем на поворот! Эти фразы радуют своим несказанным идиотизмом. Между тем изощренный физик-теоретик сумеет дать им кое-какое разумное истолкование. Чтобы уяснить это, нам придется заглянуть в геометрические первоосновы. Заодно мы поймем, что такое кривизна пространства. Ножницы, глобус, седлоВот вопрос: «прямое» и «кривое» — как отличить одно от другого? И что такое вообще кривизна и прямизна? Прямой хочется назвать линию, которая проложена по кратчайшему расстоянию между двумя точками, а кривой — ту, что обходит прямую. Не зря ведь говорят: «объехать по кривой». Поэтому понятие прямизны тесно связано с понятием расстояния. Теперь поймите главное: никакое расстояние не существует само по себе. Оно всегда отмеривается по чему-то конкретному — по дороге, по тетрадной странице или горному склону, либо, скажем, по световому лучу или по веревке, туго натянутой в пустоте. Геометры говорят абстрактно и обобщенно: расстояния отмериваются по линиям, по поверхностям, в пространстве. Физики, соглашаясь с геометрами, помнят, однако, что все эти геометрические термины отражают реальные свойства нашего мира. Кроме того, физик вкладывает свое определенное содержание в слово «отмеривать». Он помнит, что любое измерение требует не только математической корректности. Необходимы еще соответствующие приборы— линейки и часы. Да, именно часы — ведь никакое измерение нельзя даже мысленно исполнить мгновенно, это мы с вами хорошо уяснили в десятой главе, когда рассуждали о предельности скорости света и других особенностях эйнштейновского толкования природы. Таким образом, определение расстояний, как и всякий измерительный процесс, — совершенно очевидное физическое исследование. Тут геометрия зримо оборачивается физикой, физикой пространственных движений. Пока, впрочем, забудем о часах. Допустим, что мы умеем измерять длины мгновенно. Это разрешено в физике медленных по сравнению со светом движений, в физике Ньютона. И поставим первую простенькую задачку. Пусть даны две точки А и В — концы разведенных и крепко свинченных ножниц. И пусть расстояние между ними нужно определить по поверхности. Сразу задаем вопрос: по какой поверхности? Ну, сперва по шаровой. Хорошо. Подставим под ножницы глобус. Кратчайшее расстояние на его сфере физик проведет вдоль нити, натянутой между A и В по шаровой поверхности. Оно отмеряется, очевидно, не прямой линией, а кривой — дугой большого круга. Далее. Посадим наши точки на какую-нибудь седловидную поверхность. Расстояние, проложенное туго натянутой ниткой, будет пройдено по другой кривой линии — гиперболе. Если же концы ножниц приложить к поверхности письменного стола, то расстояние между ними отмерится по линии, которую мы привыкли называть прямой. Вот, кажется, добрались до прямизны. Срезав ножом седло или шар, получаем поверхности, в которых линии кратчайших расстояний — наикратчайшие. Так как будто? Но можно ли быть абсолютно уверенным, что линия на столе абсолютно прямая? И что сам стол плоский? Кажется, вопросы надуманные. Кажется, плоскость потому и плоскость, что она прямее всех поверхностей. В действительности дело обстоит сложнее. Все зависит от пространства, в котором стоит наш стол. Само пространство, с точки зрения геометра, вправе быть искривленным. И в конечном счете именно от кривизны пространства зависят кратчайшие расстояния. Я — блинДля новичка это очень странные слова — «кривизна пространства». Чтобы привыкнуть к ним, ответим сначала на несколько риторических вопросов. Как мы узнали, что глобус круглый? Посмотрели на него со стороны, из окружающего пространства. Как мы узнали, что классная доска прямая? Взглянули на нее откуда-то сбоку, опять-таки из окружающего пространства. А как узнать, прямое ли само пространство? И на пространство «поглядеть сбоку»? Но это невозможно. Нельзя покинуть пространство, выйти из него, как из дома, чтобы полюбоваться на него издали. Как ни убегай из него, все равно останешься в нем же. Выходит, нет способов определить, кривое пространство или прямое? Попробуем все же поискать их. Попробуем исследовать пространство изнутри, не выходя из него. Но не сразу. Я сперва расскажу, как решается аналогичная задача для поверхности: постараюсь узнать, какова поверхность, не глядя на нее «сбоку», а находясь непосредственно на ней. Ради наглядности я готов «разбиться в лепешку». Буквально так. Смотрите: я полностью теряю свой рост, объем, превращаюсь в бесконечно тонкий блин и оказываюсь либо на сфере, либо на седле, либо на плоскости — сам не знаю где. В качестве этого поверхностного новосела я получаю от вас задание: не сходя с поверхности, определить, какова она. Условия задания. Сперва — затрудняющие. Допускается, что я — маленький блин, а поверхность большая, причем в сколь угодно малых участках она сколь угодно мало отличается от плоскости. Кроме того, я близорук, а потому могу обследовать, не сдвигаясь с места, только ближайшие участки поверхности. И вижу лишь то, что находится на ней. А вот условия, облегчающие решение. Ползать по поверхности мне разрешено, и сколь угодно далеко. Наконец, считается, что я разумный блин. Умею рассуждать и чертить геометрические фигуры. Что же мне, блину, делать? А вот что. Пересечение параллельныхЯ намечаю на поверхности две точки — А и В. Соединяю их туго натянутой, но не отделяющейся от поверхности ниткой. По этой нитке провожу линию. И называю ее прямой. Основания для такого названия у меня есть: во- первых, линия идет по кратчайшему расстоянию между А и В, а во-вторых, из-за сугубой близорукости я вижу вокруг себя плоские участки поверхности. Это, естественно, наводит меня на предположение, что и вся она плоская. Затем я ставлю на поверхности произвольную точку С, не лежащую на прямой АВ, и пытаюсь провести через нее прямые линии, которые нигде не пересекутся с моей первоначальной прямой. Я усердно работаю. Ползаю туда-сюда, тяну нитки, провожу линии. В конце концов построение закончено. И я прихожу к одному из трех выводов: Через точку С проходит только одна прямая линия, не пересекающаяся с АВ. Удается построить сколько угодно таких линий (прямейших, но не прямых). Нет ни одной прямейшей линии, которая, проходя через С, не пересекалась бы с АВ. В первом случае моя поверхность — наверняка плоскость. Во втором — седло или какой-нибудь граммофонный раструб. В третьем — сфера либо что-нибудь вроде яичной скорлупы. Вот смотрите сами: 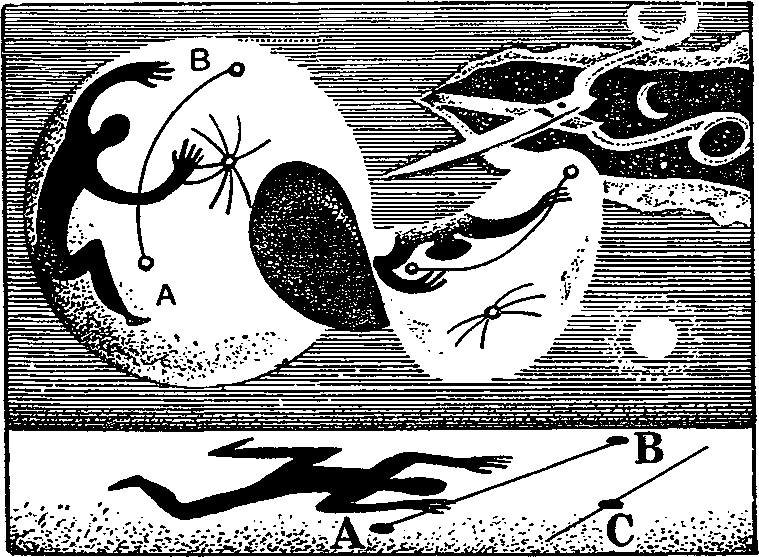 При взгляде «со стороны» лишь для плоскости оправдалось как будто название «прямая» в применении к кратчайшей линии. На непрямых же поверхностях кратчайшие расстояния отмерились по кривым. Вслед за геометрами я называю их геодезическими (сюда относятся, например, экватор и меридианы глобуса, а параллели не относятся: не по ним отмериваются на земном шаре кратчайшие расстояния). Что такое метрикаЯ все еще блин. Побывал на сфере и седле, теперь переведен на плоскость. Хлопочу о возврате высоты и объема, но пока безуспешно. И от нечего делать занимаюсь геометрией. Это тем более любопытно, что мне на плоскость прислали два отличных инструмента — транспортир и мерную рулетку. Могу измерять длины и углы (по-прежнему — мгновенно, то есть в рамках классической физики). Отправной пункт моих рассуждений — тот самый постулат о единственности прямой, не пересекающейся с данной прямой, по которому без всяких доказательств устанавливается, что поверхность — плоскость. В давние времена великий греческий геометр Евклид вывел из этого постулата всю геометрию плоскости — планиметрию.  Следом за Евклидом я строю углы, треугольники, квадраты, делаю всевозможные отсчеты, доказываю теоремы. Постепенно я убеждаюсь, что на плоскости действует строгая система правил измерения расстояний. Геометры называют эти правила метрикой. Метрические теоремы — не новинка для любого восьмиклассника. Главная из них — теорема Пифагора, знаменитые в поколениях школяров всех стран и наций «пифагоровы штаны». Теорема утверждает: в прямоугольном треугольнике сумма квадратов меньших сторон (катетов а и b) обязательно равна квадрату большей стороны (гипотенузы S): S2 = а2 +b2 Я, блин, горжусь, что сумел процитировать эту формулу по памяти, не заглядывая в учебник. Кроме теоремы Пифагора, предметом моей гордости служит доказательство еще одного важного утверждения из школьной программы: в любом треугольнике сумма углов строго равна двум прямым. Ни больше ни меньше. Надеюсь, и эту теорему вы не забыли. Примеряем „пифагоровы штаны"Один рассеянный ученик по ошибке принес на урок геометрии вместо тетради футбольный мяч. Пришлось ему на мяче чертить всевозможные чертежи. Но вышла незадача: углы треугольников никак не складывались в два прямых. Выходило больше. А когда задали задачку на теорему Пифагора, ученик-футболист аккуратно составил из геодезических линий прямоугольный треугольник, измерил стороны, сложил квадраты катетов — и получилось больше, чем квадрат гипотенузы! «Пифагоровы штаны» оказались велики для футбольного мяча. Примечательный случай произошел также с одним бравым ковбоем. Он воспылал симпатией к геометрии, но вместо тетради делал построения на лошадином седле. Тут сумма углов треугольника получилась меньше двух прямых, сумма же квадратов катетов — меньше квадрата гипотенузы. На седло «пифагоровы штаны» не натянулись. Они для седла малы. Почему же? Разве теорема Пифагора не везде справедлива? И теорема о сумме углов треугольника тоже не универсальна? Да, это так. Метрические правила неодинаковы на поверхностях разной кривизны. Они ведь выводятся из первоначального постулата о пересечении геодезических линий. На сфере, на седле, на плоскости эти линии пересекаются по-разному — отсюда разные суммы углов треугольников и усложненные (геометры говорят — обобщенные) варианты теоремы Пифагора. Разгадка поверхностиНа плоскости — проще всего. Там все точно по Евклиду. А поэтому строгое соблюдение школьных теорем — верный признак плоскости. Какие треугольники ни строй, всегда сумма углов равна двум прямым. Какие прямоугольные треугольники ни приставляй к расстоянию, всегда соблюдается равенство квадрата гипотенузы сумме квадратов катетов. Жаль, что, будучи блином, я сразу не захватил с собой рулетку и транспортир. Имея их, я не возился бы с пересечением геодезических, когда определял, какова моя поверхность. Не ползал бы, не уставал. Начертил бы треугольник, посчитал бы сумму углов, вышло два прямых — значит, моя поверхность плоская. Или сделал бы проверку по теореме Пифагора. Совпала сумма квадратов катетов с квадратом гипотенузы — есть доказательство плоскости. Будь моя поверхность неплоская, вышло бы как у геометра-футболиста и геометра-ковбоя. Сумма квадратов катетов больше квадрата гипотенузы («пифагоровы штаны» велики) — значит, я на шаре. Сумма квадратов катетов меньше квадрата гипотенузы («пифагоровы штаны» малы) — значит, я на седле. Аналогично с суммой углов треугольника. Больше она двух прямых — треугольник начерчен на сфере, меньше — на седле. Надеюсь, сказанное до сих пор не внушило вам недоверия. Пока шли разговоры о поверхностях, ничуть не удивительно, что их кривизна связана с метрикой. Это — как резиновая игрушка «уйди-уйди». Вообразите, что тетрадная страничка с геометрическими чертежами тоже резиновая, раздуйте ее в пузырь, натяните на седло или бублик — размеры углов и длин на чертежах тотчас станут другими. Ничего странного[15]. Но через эти простые вещи мы с вами подходим к неизбежности труднейшего логического скачка — с кривой поверхности в кривое пространство. К определению его кривизны изнутри, без оценок «со стороны». Глава 22. ВДОЛЬ ПРОСТРАНСТВА От окна до киоскаЯ уже не блин. Мне возвращена высота. Я покинул мир тесных, бесконечно тонких площадей, живу, как и вы, в объеме, в глубоком, раздольном пространстве. Хорошо! Есть где развернуться! Можно не только ползать, но и прыгать и летать. Это очень приятно. Но мне не до развлечений. В бытность блином я привык беспрерывно исследовать кривизну своего мира, и теперь меня тянет заняться тем же в пространстве. Прежде всего я намереваюсь придумать способ облачения пустоты в «пифагоровы штаны» и примерки к ней «треугольной шляпы». Как это сделать? Вот легонькая задачка из школьной стереометрии. От моего окна (на пятом этаже) до газетного киоска на противоположной стороне улицы «напрямую» S метров. По тротуару от моего дома с метров, b — ширина улицы, а — высоты моего окна. Требуется найти S, не мешая уличному движению — не протягивая из окна к киоску туго натянутой веревки, а вычислив это расстояние через a, b и с. Решение наипростейшее: считаем, что стена дома составляет прямой угол с поверхностью тротуара, что переход через улицу перпендикулярен к ней самой, пренебрегаем кривизной земной поверхности и дважды применяем теорему Пифагора. Так добываем формулу: S2 = а2 + b2 + с2. Вышло очень похоже на теорему Пифагора, но уже не для плоскости, а для пространства. Для кратчайшего расстояния S, прокладываемого «через пустоту». Разумеется, a, b и с можно менять, можно строить около расстояния S самые разнообразные прямоугольные треугольники. И по традиционной школьной геометрии квадрат расстояния во всех случаях будет равен сумме квадратов его трех взаимно перпендикулярных координатных отсчетов. Поэтому выражение теоремы Пифагора считается главным инвариантом евклидовой геометрии. Очень хорошо. От метрики плоскости мы шагнули к метрике пространства. Но вот существенная тонкость. Наше решение выглядит непогрешимым и единственно возможным. Однако оно предполагает самоочевидное, как кажется, условие: в пространстве существуют плоскости. Именно поэтому мы считали себя вправе дважды применить плоскую теорему Пифагора (она, как говорилось, годится в этом простейшем виде лишь для плоскостей). На том же условии нетрудно доказать и другую теорему — о том, что не только в плоских, но и пространственных треугольниках сумма углов составляет два прямых. Раз уж, согласно Евклиду, через любые три точки пространства можно провести плоскость, то и любой пространственный треугольник обязан быть плоским. Но так ли обстоит дело в действительности? Будут ли впору «прямые» штаны и «прямая» шляпа реальному пространству?
Ночью, чтобы не мешать уличному движению, я протягиваю веревку из своего окна к далекому киоску. Тщательно измеряю расстояние S. Столь же точно измеряю длины а, b и с. Возвожу их в квадрат, складываю, сравниваю. Вышло подтверждение формулы S2 = а2 + b2 + с2 — значит, в пространстве можно провести плоскости и прямые, значит, пространство плоское, евклидово. Или так. Еду на Кавказ. Стягиваю тугими канатами три горные вершины. Измеряю в этом треугольнике углы, складываю их. Получилось в сумме два прямых — есть еще одно доказательство того, что пространство плоское. Ну, а если эти эксперименты приведут к другим результатам? Если S2 не совпадет с а2 + b2 + с2? И сумма углов кавказского треугольника не даст двух прямых? Очень нелегко, очень непривычно допустить подобное. Разум упрямо противится даже мысленно позволить столь странный итог пространственных измерений. Однако вопреки протестам интуиции заставим себя вообразить, что расхождения все-таки обнаружились. Что это может значить? Когда подобное случалось на поверхности, вывод был очевиден: поверхность имеет кривизну. А когда нарушения традиционной теоремы Пифагора объявятся в пустоте, резонно будет сказать, что это доказывает кривизну пространства. Прежде, будучи блином, я с помощью метрических теорем определял, какова моя поверхность, не сходя с нее. Теперь, став объемным геометром, я хочу совершенно аналогичным способом узнать, каково пространство: насколько и как оно искривлено. И снова—не выходя из него! На сфере или седле я не мог построить плоскость и провести идеальную прямую линию. Вместо нее у меня выходили геодезические линии — прямейшие, но не прямые. Именно по ним шли кратчайшие расстояния между точками. Подобно этому, в кривом пространстве я не могу построить ни идеальной прямой, ни идеальной плоскости. Вместо плоскостей проведутся поверхности минимальной кривизны, а вместо прямых опять появятся геодезические линии — прямейшие, но не прямые. Однако изнутри, из пространства, непосредственно увидеть искривление его невозможно, потому что тамошние жители сделают кривыми все свои линейки и другие эталоны прямизны — подгонят их к располагающимся по геодезическим линиям световым лучам, натянутым нитям, путям инерционного полета тел, не подверженных действию сил, и т. д. Поверхности минимальной кривизны будут выглядеть плоскостями. Только исследования параллельных линий да метрические эксперименты помогут определить эту странную, почти невообразимую кривизну пустоты. Трудновато? Да, нелегко. Геометрическая возможность неевклидового пространства была неожиданным откровением науки XIX века. Это открытие, сделанное в 1825 году, принадлежит гениальному русскому математику Николаю Ивановичу Лобачевскому. Два варианта кривизныИтак, мы с вами добрались до кривого пространства. Научились, кажется, устанавливать изнутри его сам факт кривизны: об этом может свидетельствовать нарушение евклидовых метрических теорем. Геометры идут дальше: они умеют предсказывать, как именно изменится теорема Пифагора и сумма углов треугольника в пространствах, искривленных по-разному. Рассуждения похожи на те, что я вел, будучи блином на неизвестной поверхности. Например, если а2 + b2 + с2 меньше, чем S2, а сумма углов треугольника меньше двух прямых («пифагоровы штаны» и «треугольная шляпа» для пустоты «малы»), то пространство гиперболическое. Вместо плоскостей в нем седловидные поверхности, вместо прямых — гиперболы. Этот вариант неевклидовой геометрии и был разработан Лобачевским. Другая геометрическая система, развитая замечательным немецким математиком Георгом Риманом, получится, если а2 + b2 + с2 выйдет больше, чем S2, а сумма углов треугольника превысит два прямых. Эта геометрия называется эллиптической. В ней вместо плоскостей — поверхности вроде яичной скорлупы или мяча, вместо прямых — дуги больших эллипсов или, соответственно, больших кругов. Позволю себе повторить еще раз: в плавно искривленном пространстве все геодезические линии представляются прямыми. «Истинных» же прямых там нет, их невозможно провести. Любая неизбежно согнется, как обязательно согнется нить, натянутая по сфере. Причем, если пространство искривлено неравномерно, в разных местах по-разному, то и прямейшие геодезические линии в разных точках согнутся неодинаково. При движении вдоль геодезической ее «волнистость», конечно, незаметна. Всюду эта линия выглядит одинаково прямехонькой. Однако стоит испытать в разных местах метрические правила, как обнаружатся изменения, отклонения от привычной евклидовой «нормы». Короче говоря, в неравномерно-неевклидовом пространстве от точки к точке меняется метрика, приемы определения расстояний. Меняется теорема Пифагора. В общем виде простая формула ее заменяется более сложной, включающей величины, которые характеризуют кривизну пространства в разных его местах. И, как следствие, в разных местах такого пространства оказываются разными длины предметов, кратчайшие расстояния между точками. Вот такие чудеса допускают геометры в неевклидовом пространстве! Сфера ПуанкареЕще диковина: некоторые неевклидовы пространства могут быть конечными, хоть и безграничными. Расстояния там не превышают некоего определенного значения и, соответственно, не могут существовать сколь угодно большие объемы. Подобно тому, как яйцо или мяч обладают безграничной поверхностью, но ограниченной площадью, эллиптическое пространство не имеет границ и тем не менее имеет конечный объем. Искривляясь оно как бы замыкается на себя! Странно? Очень.
Но все же доступно наглядному моделированию. Французский математик Анри Пуанкаре один из предшественников Эйнштейна, ухитрился придумать любопытную модель замкнутого сферического пространства. Вот что он советует вообразить. В шаровом сосуде находится некая среда, в которой плавают предметы и существа, наделенные весьма фантастическими свойствами. При охлаждении и среда и предметы абсолютно одинаково сжимаются, причем при нуле градусов обращаются в точки. Кроме того, световые лучи в этой среде преломляются тем сильнее, чем ниже температура. Шар снаружи заморожен до нуля градусов. А изнутри, из центра, разогрет. И от центра к периферии температура плавно снижается. Еще условие: существо в шаре не должно ощущать перемен температуры. Ему всегда «не жарко, не холодно». Вот и все. По вашей командировке я обретаю указанные свойства, переселяюсь в шар Пуанкаре (пусть висящий где- то в космосе, в невесомости) и, допустим, обитаю в нем в полном одиночестве. Тем не менее я замечаю вокруг множество человеческих фигур. Всюду я вижу себя и только себя — и впереди, и сзади, и со всех сторон. Световые лучи идут замкнутыми путями. Приближаясь к краям шара, они, плавно преломляясь, заворачивают внутрь, так что эти края невозможно увидеть, даже находясь совсем рядом с ними. Завернув, лучи возвращаются туда, откуда вышли. Вот и получается, что передо мной — моя спина, надо мной — подошвы моих ног, подо мной — моя макушка. Стреляя вперед из светового пистолета, я, если захочу, попаду в собственный затылок. Разумеется, луч представляется мне прямым. Считая его эталоном прямизны, я не замечаю кривизны своего пространства. Ее нельзя обнаружить и движением: шагая вдоль луча, я открываю лишь существование предельно большого расстояния, так как вскоре возвращаюсь к месту старта. Стенки шара мне совершенно недоступны. Когда я подхожу к ним, то сжимаюсь вместе с окружающей средой, и одновременно сжимаются все расстояния вокруг меня, все длины, все высоты. В любой точке шара я не замечаю изменения своих размеров. Поэтому всюду я воспринимаю окружающее пространство так, будто нахожусь в его центре. И не вижу нигде никаких границ своего маленького мирка. Он конечен по объему, но для меня безграничен. Очень красивая модель! Как это ни парадоксально, шар Пуанкаре, быть может, кое в чем схож с нашей необозримой Вселенной. Но об этом потом. Обруч и рельсПолагаю, мы с вами уже созрели для геометрического истолкования анекдота о кривых дровах. Очень просто: если паровоз въезжает из плоского евклидова пространства в любое неевклидово, то прямые дрова автоматически превращаются в кривые. Наоборот, если паровоз шел в неевклидовом пространстве и дрова в нем, по мнению машиниста и кочегара, были прямыми, то при въезде в евклидово пространство они искривятся. Кривизна и прямизна предстают перед нами свойствами не абсолютными, а относительными! Каждое из них зависит от точки зрения, от договоренности, продиктованной, правда, не свободным произволом, а геометрическими свойствами пространства. Вообразив, что пространства разной кривизны вложены друг в друга и из одного можно наблюдать другое, относительность кривизны удастся представить вполне наглядно. Допустим, например, такой случай. Изготовляя шар Пуанкаре, я вмонтировал в него резиновое кольцо. В евклидовом пространстве это кольцо мне представляется безусловно кривым. Но в шаре Пуанкаре оно может стать прямейшим, если вдоль него пойдет луч света. Вместе с тем железнодорожный рельс, для меня прямой как стрела, в сферическом пространстве станет дугой — ведь «прямой» для обитателя шара Пуанкаре световой луч от рельса отклонится. Удивляйтесь, если не устали! Такова в самых примитивных чертах неевклидова геометрия. Заканчивая беседу о ней, я должен сообщить вам нечто важное и несколько обескураживающее. Как вы наверняка догадываетесь, описанные в этой главе геометрические странности имеют непосредственное отношение к общей теории относительности, к тяготению, к инерции, в конечном счете — ко все еще не разгаданной нами до .конца загадке падения тел, действию тяжести через пустоту. Это действительно так. Но связь, к сожалению, далеко не столь проста, как хотелось бы любителям легкого бегства от удивлений. Приготовьтесь к разочарованию. Все, буквально все только что изложенные геометрические рассуждения и примеры в мире Эйнштейна не имеют ни грана физического смысла. Ибо с самого начала этой главы мы с вами разрешили себе непозволительную идеализацию истинного положения вещей — признали возможность мгновенного измерения расстояний. Отсюда выросла физическая небылица: пространство, не зависимое от времени. На самом деле ничего мгновенного в природе не бывает. Измерения расстояний кроме линеек требуют еще и часов. И строгого соблюдения не только геометрических, но и чисто физических правил, говорящих, в частности, о том, что пространство вообще не может существовать вне времени. В реальном мире пространство и время неразделимы. Как велики последствия этого, вы скоро поймете. Глава 23. ВДОЛЬ МИРА О пользе чистотыВ начале двадцать первой главы я пропел панегирик геометрии. Потом долго втолковывал вам всякие странные геометрические идеи, а затем объявил, что они лишены физического смысла. Получилось вроде бы не очень последовательно. Зачем же понадобились эти разговоры? Дело в том, что сама по себе геометрия, как и любая чисто математическая наука, слишком абстрактна, слишком узка, чтобы служить надежным зеркалом природы. За гармонией линий, за сплетением идеальных фигур, за сложной очередью посылок и следствий она склонна не замечать настоящего мира. С давних пор создавалась эта рафинированная, очищенная от реальности, всеядная, применимая к чему угодно символическая логика. Чистой математике все равно, что считать. Лишь бы считать. Шли века, и геометрия развивалась двумя путями. С одной стороны, теснее и теснее сближалась с практикой, училась виртуозности в решении практических задач. Но одновременно все дальше уходила от действительности, все глубже погружалась в мир математических грез. Именно на этом пути она отыскала неевклидовы пространства. Я думаю, так будет всегда. Несколько утрируя и упрощая, можно сказать: академически-изысканный геометр-теоретик никогда не заинтересуется вплотную физической подоплекой своих построений. Главное для него — чтобы открывались новые и новые логические шаги, чтобы неизменно соблюдалась твердокаменная строгость, ветвилось дерево безупречно точных, растущих друг из друга абстракций. Хорошо это или плохо? Великолепно! Ведь это полное освобождение математической мысли, широчайший простор для логики, труднейшая тренировка и строжайший экзамен человеческому уму. Но ведь логична не только математика. Природа тоже логична. Во всем, всегда и весьма строго логична. Вот почему поиски «чистых» математиков просто не могут быть бесполезными для естествознания. Рано или поздно абстрактнейшие математические упражнения становятся источником находок, драгоценных для естествоиспытателей. Стало законом: любая новая физическая теория опирается на заранее открытый, предварительно подготовленный математический аппарат. «Чистые» математики стараются не зря. Это в полной мере касается общей теории относительности. Ее фундамент — дополненное, одухотворенное физикой учение о неевклидовых искривленных пространствах, то самое, что было основано гением математиков за девяносто лет (!) до первых догадок Эйнштейна. Эксперимент ГауссаПолезно проследить, как от физической небылицы неевклидова геометрия поднялась до почетной персоны, олицетворяющей остов реального мира. История эта началась в середине прошлого века, когда идеи о кривизне пространства стали постепенно проникать в научное сознание. Одновременно с Лобачевским их проводником был талантливый венгр Янош Больяй, затем — немец Георг Риман. Маститые коллеги скептически, а то и иронически относились к их трудам. Кривизна прямейших линий представлялась совершенно беспочвенной фантазией, фикцией, измышлением, чрезмерно абстрактным даже для чистой математики. Все-таки семя было брошено. И начало давать ростки. Мало-помалу привыкая к парадоксальной геометрической гипотезе, ученые закономерно пришли к мысли: а не проверить ли ее? Не откроется ли в большом то, что незаметно в малом? Так родился замысел физико-геометрического эксперимента вроде того, о котором я уже упоминал в предыдущей главе, во время популяризаторского галопа в неевклидовом пространстве: измерить сумму углов какого-нибудь гигантского треугольника. Карл Фридрих Гаусс, знаменитый немецкий математик, предпринял ради этого обширную геодезическую экспедицию. Световым лучом были связаны три горы — Брокен, Высокий Хаген и Инзельберг. Горные вершины стали геометрическими вершинами треугольника. Тщательные измерения его углов дали в сумме традиционные евклидовы два прямых — как и на классной доске. Эксперимент утвердил Евклида в масштабах Тирольских Альп. И как будто опроверг идею пространственной кривизны в тех же масштабах и в пределах точности угломерных инструментов. Можно было думать, что если кривизна пространства и существует, то обнаружить ее удастся либо более точным измерением углов, либо в треугольнике еще более крупного масштаба — скажем, астрономического, с вершинами, лежащими на каких-нибудь звездах. Так считалось много десятилетий, пока в умах ученых царила физика Ньютона с ее вечно неизменным абсолютным пространством, с возможностью (хотя бы принципиальной) сколь угодно быстрых путешествий и измерений. А потом явился Эйнштейн. Мгновенные путешествия и измерения получили отставку. И выяснилось, что эксперимент Гаусса некорректен, несовместим с физикой мира. Его нельзя исполнить даже мысленно[16]. Не забывать о времени!Приговор был таков: в малых масштабах, где мир бесспорно евклидов (это видно во всех школьных тетрадках), мгновенное творение и измерение светового треугольника не даст ничего нового — там и кривизны практически нет. А в крупных, астрономических масштабах ни Гаусс, ни потомки его, вооруженные новейшей техникой, просто не поспели бы сделать желаемых измерений. Пока световой луч, «вычерчивая» гигантский космический треугольник, бежал бы от звезды к звезде, он вместе с тем «поднимался» бы в будущее. Это сделало бы невозможным возврат в точку старта — ведь вспять во времени двигаться запрещено во имя исполнения принципа причинности. Но может быть, сама точка старта, равномерно «поднявшись» в будущее, совпала бы с финишем луча, обежавшего треугольник? В частном случае, при неизменно равномерном времени, это допустимо. Но в общем случае это невозможно, потому что, как объяснялось в девятнадцатой и двадцатой главах, вместе с деформацией пространства происходит деформация времени. Точка старта, двигаясь в будущее, могла пережить изменения темпа времени и встретиться с вернувшимся лучом совсем не там, где произошла бы эта встреча, будь время неизменно равномерным. Строго говоря, в крупных, астрономических масштабах вообще невозможно построить пространственный треугольник. Он распадется при «черчении». И, значит, невозможно измерить его углы. И, следовательно, невозможно определить кривизну пространства. Такова же причина объявленной нефизичности всех примеров двадцать первой главы. Нет в эйнштейновской физике «независимого», «самостоятельного» пространства. Тут снова отчетливо проступает существеннейшая черта идей Эйнштейна: неразделимость пространства и времени, их тесное единство. Только в специальных, нарочно придуманных случаях могут быть исключения — скажем, прямое время в искривленном пространстве (один из таких примеров — эйнштейновская космологическая модель Вселенной-—будет разобран в двадцать шестой главе). А как правило, деформация пространства обязательно сопровождается деформацией времени. Из этого и надо исходить при физическом осмыслении идей неевклидовой геометрии. Короче говоря, раз уж есть где-то в мире кривизна, то она присуща сразу и пространству и времени. Эволюция аквариумовСнова коротенькое воспоминание. Прочтите его не спеша и хорошенько прочувствуйте. Много страниц назад, рассуждая о воззрениях Ньютона, я уподобил классическую систему пространственного отсчета гигантскому жесткому аквариуму. Он был незыблемо неподвижен, ибо покоился на неподвижных звездах. И относительно его дна и стенок можно было мгновенно отмеривать расстояния в абсолютном евклидовом пространстве. На аквариуме висели нематериальные звездные часы, отсчитывающие всеобщее, везде одинаковое, равномерное математическое время. Это был божественный остов ньютоновского мира. При движении тел их пространственные координаты (расстояния до дна и двух стенок аквариума) непрерывно менялись, для разных тел по-разному. Время же для всех тел текло совершенно одинаково. Из-за этого пространство мыслилось независимым от времени. Таким оно пребывает и до сих пор в наших головах, потому что очень трудно выбить привычку жизни в мире Ньютона — в мире движений, медленных по сравнению со светом.
Затем, когда на арену выдвинулись быстрые движения, когда были запрещены скорости, превышающие световую, аквариум рухнул. Вместе с ним исчезли абсолютное время и абсолютное пространство. Эйнштейн выдвинул вместо них относительные пространства и относительные времена — свои для каждого тела, движущегося по инерции равномерно и прямолинейно. Можно сказать так: у всех таких тел появились собственные аквариумы, движущиеся вместе с ними по прямым равномерно, не быстрее света. Они остались вполне жесткими и прямыми, эти «индивидуальные» аквариумы. Но, во-первых, масштаб длины в любом из них стал неабсолютен — укорачивался для движущихся наблюдателей. И, во-вторых, для движущихся наблюдателей замедлился темп хода часов, висящих на аквариумах. Так вместо движений, происходящих в абсолютном пространстве и едином математическом времени, появились движения в собственных и релятивистских временах и пространствах, соединенных неразделимо. Чтобы изображать их графически, мы построили диаграмму. Это был мир Минковского[17]. К Каждому событию принадлежала четырехмерная мировая точка — три собственных пространственных отсчета и собственный отсчет времени. Для иначе движущихся систем все четыре отсчета этого же события были другими. Но в любой из этих систем отсчета, летящих относительно друг друга равномерно по прямым, квадрат интервала между двумя событиями сохранялся неизменным. Последнее утверждение — знаменитая инвариантность интервала. Из нее Эйнштейн извлек все формулы частной теории относительности, все эти удивительные парадоксы, проиллюстрированные у нас приключениями Клио, недоразумениями с космической торговлей и т. д. Вплоть до закона эквивалентности массы и энергии и предсказания атомной бомбы. Кривой мирДалее мы посетовали, что, несмотря на красноречивые успехи специальной теории относительности, она все же далековата от действительной природы: не было тяготения, пронизывающего Вселенную. И тогда мы вспомнили о жерновах и песчинках. О странной особенности их совместного падения, подмеченной еще Галилеем, о необъяснимом у Ньютона равенстве тяжелой и инертной масс. После обмана Людмилы космическим Черномором мы провозгласили эйнштейновский принцип эквивалентности инерции и тяжести. Выслушав возражения Маленького Принца, признали сугубую локальность этого принципа. Но потом побывали на сотой Олимпиаде и выяснили, что, несмотря на свою ограниченную применимость, принцип эквивалентности вместе с выводами специальной теории относительности ведет к знаменательному и неожиданному утверждению: масса деформирует пространство и время. Наконец мы научились понимать слова «искривление пространства». Постигли кое-что в неевклидовой геометрии. Согласились, что движение материи должно сопровождаться деформацией пространства — времени. Массы вещества искривляют саму диаграмму движения. Я нарочно столь назойливо, не стесняясь повторений, навязываю вам эту истину. Иначе трудно осмыслить главную идею общей теории относительности, к которой мы уже подошли вплотную. Вот она. Тела, летящие по инерции, движутся не по прямым линиям несуществующего ньютоновского абсолютного пространства. Мировые линии их располагаются не по прямым упрощенного мира частной теории относительности, лишенного тяготения. В общем случае тела, летящие по инерции, следуют геодезическим линиям реального искривленного пространства — времени. Толкните камень, уроните его, подбросьте — его движение изобразится четырехмерной геодезической линией, которая располагается на диаграмме поперек линий одинаковой кривизны пространства — времени. Там, где геодезическая искривится, камень приобретет ускорение. Причем сам, без всяких усилий, приложенных со стороны. Ибо такой путь на диаграмме будет для него наиболее прямым. Этот четырехмерный путь будет, однако, не кратчайшим, а, как ни странно, длиннейшим. Самым прямым, но самым длинным! Ибо именно по длиннейшим расстояниям идут четырехмерные геодезические линии в мире пространства — времени. Совсем не так, как на глобусе или седле! Вот вам очередной парадокс. Впрочем, в нем нет ничего нового. Ведь речь идет не об обычном пространственном пути. Мы говорим о линии на графике пространства — времени, построенном по рецептам теории относительности. А для разных относительных скоростей на этой диаграмме — разные масштабы длин и длительностей. Тут сойти с геодезической— значит ускориться под действием силы. И следовательно, попасть во власть относительно «укороченных» километров и «удлиненных» секунд. Тот же, кто движется строго по геодезической (то есть только по инерции), преодолевает «наиболее длинные» километры, тратя на это лишние «коротенькие» секунды. Потому-то, кстати, и получается парадокс близнецов — движение по инерции между двумя мировыми точками обязательно дольше, чем полет по тому же пространственному пути с ускорением и замедлением. С легкой руки английского философа Бертрана Рассела это своеобразие называют иногда «законом космической лени». Он действует и в мире, искривленном массами планет и звезд. Падение камня, обращение лун и спутников — это «самое ленивое» движение: по длиннейшим, хоть и прямейшим, но согнутым геодезическим линиям. В последних абзацах — суть теории тяготения Эйнштейна. В них спрятана долгожданная разгадка чудес падения: таинственного «действия без прикосновения» и равной быстроты летящих с Пизанской башни ядер и пуль. В них же немало других физических откровений, вплоть до указаний на устройство всей Вселенной. Миновав лабиринты недоумений, рогатки логических трудностей, ухабы парадоксов, мы с вами наконец-то видим финиш длинной и извилистой трассы бега от удивления загадочному поведению падающего камня. Глава 24. ПОЧЕМУ ПАДАЕТ КАМЕНЬ Моллюск отсчетаМой труженик-читатель, которому я искренне сочувствую и которого от души благодарю за то, что он добрался-таки до этой главы, наверное, устал. Поэтому остатки нашего книжного пути проследуем не торопясь. Честно говоря, тут надо бы сделать даже остановку, и длительную — лет этак на пять — десять, с тем чтобы засесть за учебники и проштудировать весьма сложный математический аппарат, без которого немыслимо уяснить количественные выводы эйнштейновской теории тяготения. Отказываясь от этого экскурса, мы обрекаем себя на очень приблизительное ее понимание. Все же качественная сторона проблемы при вдумчивом и неспешном чтении нижеследующего может стать, мне кажется, вполне ясной рядовому девятикласснику. А то и восьмикласснику. Собственно говоря, основное содержание эйнштейновских взглядов на природу тяготения вам уже известно (курсив на странице 232). Остаются подробности и тонкости. Разберемся, какова в общей теории относительности судьба систем пространственно-временного отсчета. Это знакомые нам «индивидуальные» аквариумы специальной теории, но они изменили строение и форму. Часы же, висевшие на каждом аквариуме, размножились в огромное число раз. Системы отсчета потеряли жесткость — стали гибкими, растяжимыми, ячеистыми. Вместо жесткого аквариума, вместо твердого трезубца пространственных координат, увенчанного единственными часами, появился, по выражению Эйнштейна, моллюск отсчета. Вообразите мягкую каучуковую губку, которая невидима, неощутима. Она огромна — величиной со Вселенную, однако связана каким-то образом с телом, движущимся как угодно, и движется вместе с ним. Эта губка состоит из бесчисленных крошечных ячеек. Каждая ячейка — участочек прямого пространства и равномерного времени (для наблюдателя, движущегося вместе с этим участком). Еще лучше представить себе, что никаких ячеек нет — просто в бесконечно малом пространстве губка не имеет кривизны и темп времени в достаточно близких точках различается бесконечно мало. Но в крупных масштабах заметна пространственно-временная четырехмерная кривизна. И она от ячейки к ячейке, от точки к точке плавно меняется. Вот это неевклидово пространство, привязанное к определенному движущемуся телу и заполненное (мысленно) множеством часов, идущих в плавно меняющемся темпе, и есть эйнштейновский моллюск. Трепетная, чуткая система отсчета. Состояние ее зависит от масс, распределения и движения вещества. В таком моллюске и происходит реальное физическое движение. Оно изображается графиками мира событий— на четырехмерной диаграмме Минковского, которая тоже искривлена. Геодезическими линиями ее, тут прямыми, там изогнутыми, определяется движение по инерции планет, спутников, камней. В том числе и падение. Падение — только по инерции! Соль тут заключается в следующем: отсутствует то, что мы привыкли называть силой тяготения. Камень не притягивается Землей. Он по инерции движется вдоль четырехмерной геодезической, а вблизи Земли эта геодезическая изогнута так, что «втыкается» в мировую линию поверхности планеты. И камень, летя с башни по инерции, падает на Землю. Штаны для мираПока наши разговоры о моллюске отсчета, сменившем старый аквариум, не более, чем слова. Пока есть только изложение замысла. Реализовать замысел — значит указать, каков моллюск, каковы конкретно закономерности изменений его формы, как она зависит от заполняющего его движущегося вещества. Поставив перед собой эту цель, Эйнштейн шел к ней долго, с исключительным упорством. Надо было влить математическое содержание в идею кривизны четырехмерной пространственно-временной диаграммы. Дать формулы для ее вычисления и, как следствие, для предсказания движений тел в реальном мире. Отправным пунктом работы послужила общая математическая характеристика кривизны — не что иное, как усложненная и обобщенная форма хорошо знакомой нам теоремы Пифагора. Напомню, что эта теорема — метрическая, то есть содержит в себе рецепт определения расстояний. На плоскости она имела простейший школьный вид: S2 = а2 + b2 На искривленной поверхности изменилась: S2 стало не равно S2 = а2 + b2. Не стоит выписывать измененной формы этой теоремы. Скажу лишь, что для определения квадрата расстояния на любой искривленной поверхности а2 и b2 надо на что-то умножить да еще в формуле появится член с произведением а на b. (Тут к тому же а и b будут бесконечно малыми величинами.) Аналогично изменится вид трехмерной теоремы Пифагора в изогнутом трехмерном пространстве. А в мире Минковского? На четырехмерной диаграмме быстрых движений? Эта диаграмма строилась на основе постулатов Эйнштейна. В результате на ней отобразилась связь пространства и времени: появились гиперболические калибровочные линии, отсекающие на разных осях разные масштабы длин и длительностей. Это определило выражение для квадрата интервала (то есть, опять напоминаю, расстояния между двумя событиями в четырехмерном пространственно-временном мире). В двенадцатой главе оно было записано так: S2 = l2 – c2t2. Расшифровав по «прямой» пространственной теореме Пифагора l2 как сумму х2 + у2 + z2, получим: S2 = х2 + y2 + z2 — c2t2.Очень похоже на теорему Пифагора, только четвертое слагаемое отрицательно. Но от этого можно избавиться. Ради симметрии сделаем замену: вместо -c2t2 будем писать ?2. Тогда сходство, во всяком случае по математической форме, будет полным. Таково метрическое правило для измерения интервала на диаграмме частной теории и относительности — без учета тяготеющих масс. Тут мир не имеет кривизны. Ну, а в искривленном мире выражение интервала усложнится — подобно тому, как усложнилась теорема Пифагора на шаре или седле. Каждый член правой части формулы на что-то умножится, появятся члены с произведениями ху, хz и т. д. Что же получится? Дабы подчеркнуть неравномерную кривизну мира, все отсчеты снабдим значком ? (дельта) — это будет означать, что измерения ведутся в достаточно малой области мира, где кривизна его остается постоянной. И тогда (поверьте на слово) интервал между двумя близкими событиями в искривленном мире пространства — времени будет выглядеть так: ?S2 = g11?x2 + g22?y2 + g33?z2 +g44??2 + 2g12?x?y + 2g13?x?z + 2g14?x?? + 2g23?y?z + 2g24?y?? + 2g34?z?? Множители g, снабженные парой индексов (от 1 до 4), — коэффициенты кривизны. Их всего десять. От них-то, в конечном итоге, и зависит искривление мира. А сами они зависят от масс и расстояний до окружающих тел. Написанное выражение носит громкий и почетный титул — фундаментальный метрический тензор. Отметив музыкальную звучность термина, воздержимся от расшифровки его смысла (это чистая математика). По существу, здесь не что иное, как усложнение и обобщение «покроя» школьных «пифагоровых штанов» на случай искривленного четырехмерного мира, диаграммы движения в эйнштейновском моллюске отсчета. В далекой от звезд и планет пустоте при равномерном движении моллюск обращается в аквариум и никакой кривизны мира нет. Фундаментальный метрический тензор становится интервалом специальной теории относительности. В этом случае (при обратной замене ?2 на —c2t2) g11 = g22 = g33 =1, g44 =-c2, a g12 = g13 = g14 = g23 = g24 = g34 =0 Там же, где нет вокруг полной пустоты, где сравнительно недалеки звезды и планеты, должны иметь место отклонения от этих «нормальных» значений метрических коэффициентов. Эллиптическая кривизнаСледующий шаг — разгадка математической зависимости между метрическими коэффициентами и массами движущегося вещества. Шаг труднейший. Коэффициентов — десять. Значит, нужно написать систему из десяти уравнений, связывающих эти коэффициенты с массой и расстояниями от точки наблюдения до окружающих тел. Гений и труд Эйнштейна отыскали эту систему — систему мировых уравнений. Нам с вами не стоит даже пытаться разбирать логику вывода и выписывать уравнения. Удовлетворимся сообщением, что они существуют. Еще сложнее и тоньше дальнейшая работа — решение системы мировых уравнений. Тут Эйнштейн и его последователи столкнулись с трудностями поистине титаническими. До нашего времени задача полностью не решена. Добыты только отдельные частные решения, годные лишь ограниченно, при всевозможных упрощениях. Тем не менее результаты огромны: создана математическая теория тяготения, в которой действительно нет, как таковой, силы тяготения! Есть только силы инерции. Грубо говоря, дело обстоит следующим образом. Удалось выяснить, как именно отклоняются от «нормы далекой пустоты» метрические коэффициенты мира около тяжелого тела — например, Земли. На этом материале был установлен «околоземной вариант» фундаментального метрического тензора, то есть, другими словами, характеристика кривизны пространства — времени. Оказалось, что геометрия тут эллиптическая (вроде геометрии поверхности яйца, но только, конечно, четырехмерная, да еще такая, что геодезические линии служат не кратчайшими, как на яйце, а длиннейшими расстояниями. Причем с приближением к центру Земли кривизна мира увеличивается (кривизна поверхности яйца увеличивается с приближением к его «острым углам»). И увеличение кривизны мира означает очень малое замедление времени и сокращение расстояний. Отсюда попробуем представить себе ход геодезических линий, этих прямейших длиннейших путей, «рельсов» инерционного движения тел на диаграмме искривленного пространства — времени. Во-первых, все геодезические сходятся, вроде меридианов на глобусе. Во-вторых, кривизна их тем больше, чем больше кривизна мира. Не забывайте, что речь идет о мире-диаграмме, построенном по правилам Эйнштейна, что одно из его измерений — время — может только возрастать. Поэтому геодезические линии, обладая наибольшей прямизной и наибольшей длиной, имеют, кроме того, направление — устремлены в сторону возрастания времени. Тела движутся по ним из прошлого в будущее, но не наоборот. Так вода в реке обязательно течет сверху вниз. Разумеется, вообразить все это вместе и сразу непросто. Попытаемся все же применить сказанное к поведению камня, находящегося около Земли. Камень выпущен И вот пробил торжественный час исполнить давнее, много раз повторенное обещание: окончательно объяснить чудо падения камня на Землю. Включите мысленно духовой оркестр — и, пожалуй, сразу выключите, чтобы не мешал. Внимание! У меня в руке камень. Внизу — Земля. Будем считать, что в пространстве Земля стоит на месте (движением ее вокруг Солнца пренебрежем, как и прочими астрономическими движениями). Но во времени она движется. Она мчится в будущее. И камень мчится в будущее. И я тоже. Этим бесспорным фактом удобно воспользоваться для объяснений. Земля не испытывает никаких сил (о Солнце пока совсем забудем), то есть находится во власти одной только инерции. Можно сказать: Земля по инерции движется в будущее. А камень испытывает действие силы — он удерживается моей рукой. Я разжимаю пальцы — дарю камню свободу, избавляю его от действия силы. И (внимание!) давайте теперь вообще забудем о таком понятии, как сила тяготения. Пусть камень, как и Земля, остался во власти одной лишь инерции. Что ж, тогда и камень полетит по инерции в будущее. Будь Земля бесплотна, лишена массы, мир вокруг нее не был бы искривлен и геодезическая линия освобожденного камня была бы совершенно прямой. Не получив толчка, камень благодаря инерции хранил бы покой в пространстве, передвигаясь только во времени, — спокойно висел бы возле моей разжатой руки. Обо мне можно было бы сказать то же самое. Я и камень мчались бы в будущее вместе, по соседним строго прямым и параллельным геодезическим линиям, все время находясь в относительной неподвижности. Никакого падения не случилось бы. Но в действительности Земля отнюдь не бесплотна. Мир искривлен ее гигантской массой. Поэтому я и камень неравноправны. Я испытываю действие силы — пол давит на мои подошвы, не позволяя мне «провалиться сквозь землю». Другими словами, меня все время «насильно» сдвигают с моей геодезической линии и держат на мировой линии, параллельной геодезической линии центра планеты. А камень по-прежнему свободен. На него ничто не давит. Он и теперь путешествует в будущее по своей геодезической линии. Но на этот раз она изогнута, потому что мир искривлен. Правда, пространство — время деформированы так мало, что и геодезические изогнуты совсем незначительно. В первые мгновения свободы камня его геодезическая линия почти совпадает с моей мировой линией, и камень почти неподвижен относительно моей ладони. Но бег во времени стремителен. За микросекунды «путешествия в будущее» геодезическая линия камня чуть отходит от моей мировой линии. Поэтому камень, мчась вместе со мной во времени, неизбежно набирает скорость и смещается относительно меня в пространстве. С каждым мгновением скорость и пространственное смещение камня больше, потому что его геодезическая линия все круче отклоняется от моей мировой линии. Саму кривизну мира я не замечаю, как и ее увеличения: замедление секунд и сокращение сантиметров слишком незначительны. Не чувствую я и того, как вместе с камнем и Землей мчусь в будущее: этого «полета» ведь на самом деле нет, он лишь условность, привлеченная для удобства объяснений. Поэтому движение камня по геодезической линии возле Земли предстает передо мной в явлении зримом и привычном: ускоренном движении камня к центру планеты. Так на моих глазах совершается чудо падения. Если бы я зажал в кулаке камень и песчинку, а потом одновременно отпустил их, и песчинка и камень опять полетели бы в будущее по инерции, не отставая друг от друга, ибо следовали по одной и той же геодезической. И, конечно, одновременно столкнулись бы с земной поверхностью. Никаких сил тяготения, действующих «через пустоту», как видите, не понадобилось. Не потребовалось никаких невидимых нитей и резинок между Землей и камнем. И все-таки падение состоялось. В точном согласии с давнишним наблюдением Галилея. Прыжки мячаРади большей ясности сейчас будут повторения сказанного в видоизмененных вариантах и пояснения с помощью упрощенных диаграмм. Начало координат мира пространства — времени устанавливаем на камне в момент времени t = 0. Пространство принимаем одномерным, то есть учитываем единственное пространственное измерение — ось х (ее направим вниз, не рисуя). Где-то на ней центр масс и начало мировой линии Земли. Диаграмма ньютоновского мира в этом случае такова:  Ось времени — прямая как стрела. Мировая линия камня согнута. Черными стрелками изображена сила тяготения, без нее в классике не обойтись. А вот диаграмма той же последовательности событий с точки зрения Эйнштейна — Минковского:  Ось времени камня пригнулась к мировой линии Земли. И не требуется никаких сил тяготения. Конечно, камень не обязательно просто ронять. Его можно как угодно подбросить. И система отсчета может как угодно двигаться относительно Земли и камня. Все равно он будет лететь по инерции вдоль осей времени или геодезических линий мира, искривленного массой планеты. С точки зрения старой механики Ньютона, это представится движением под действием силы тяжести. Вот, например, график движения мяча, который сначала был отпущен с полуметровой высоты, упал, ударился о землю, подпрыгнул вертикально вверх и т. д.  В каждом прыжке мяч находился примерно секунду. За это время в пространстве он пролетал метр. А во времени? На диаграмме Минковского масштаб времени множится на скорость света, то есть каждая секунда приравнивается к тремстам тысячам «километров». Такой гигантский «путь во времени» и проделал наш мяч, пока прыгал на полметра вверх и вниз в пространстве. Отклонение геодезической линии мяча от евклидовой прямой, таким образом, составляло на диаграмме пять десятитысячных долей сантиметра на «километр времени». Повторю еще раз: разумеется, никакого «километра времени» на самом деле нет—он есть только на графике движения, где время, ради формального удобства, выражается в единицах длины. Но цифра, которую мы выудили из графика Минковского, хорошо демонстрирует ничтожность искривления диаграммы мира массой Земли у ее поверхности. И именно эта неуловимо крошечная кривизна пространства — времени полностью объясняет зримое, весомое, ежеминутно творящееся на наших глазах чудо падения. Фигурально выражаясь, происходит оно потому, что уж очень быстро мы и все окружающее мчимся в будущее. Масштаб на оси времени диаграммы множится на скорость света! Поэтому несмотря на малость деформации пространства — времени микроскопическое искривление четырехмерной геодезической линии движения мяча мгновенно накапливается в величину заметную и ощутимую. Вот одно не очень удачное сравнение. Я смотрю из идущего поезда на тележку, катящуюся рядом по колее, которая круто сворачивает к колее поезда. Пусть я не чувствую, что движусь, что мчится вперед тележка, не замечаю рельсов. Я вижу одно: тележка ускоренно приближается. «Падает» на поезд! Аналогия, правда, неточная: поступательный ход поезда и тележки уподобляется бегу во времени, а это условность. Вообще надо помнить: наш реальный мир — не диаграмма. Условная четырехмерность мира — лишь математический прием, позволяющий «начертить» то, что время и пространство связаны и подчинены влиянию вещества.
Еще одно замечание — про вес. Что же такое тяжесть камня, если нет дальнодействующей, «проникающей сквозь пустоту», «таинственной», «божественной» силы тяготения? В самом начале этой книжки мы с вами предположили: тяжесть есть давление камня на опору, и только. Теперь это предположение подтверждается: вес предстает перед нами как давление камня на опору, которая не дает ему двигаться свободно по геодезической линии. Другими словами, вес — не что иное, как сила инерции. Подобной силой действовал бегун на дорожку стадиона олимпийской карусели или похищенная Людмила — на пол ускорявшейся ракеты Черномора. А теперь я сижу и силой инерции давлю на стул, который не позволяет мне по инерции улететь к центру планеты. И яблоко прикладывает силу инерции к ветке яблони, на которой висит. Знал бы это Ньютон! Видите: благодаря открытой Эйнштейном кривизне пространства — времени сила тяжести сведена к силам инерции в совершенно земных, совсем не фантастических событиях. И этот факт, честное слово, удивительнее самой экзотической литературной небывальщины. Примечания:1 Потому-то с глубокой древности начала развиваться статика— область физики, занимающаяся всякого рода неподвижностями: уравновешенными весами, блоками, рычагами. Все это вещи нужные, понимать их важно и полезно, недаром им посвятил много времени прославленный грек Архимед. Даже в неподвижности он подметил многое, что необходимо изобретателям всевозможных машин. Тем не менее, если быть придирчивым, это еще не была настоящая физика. Это была только подготовка к ней. А подлинная физика началась с изучения движений. 12 То есть теории, касающейся равномерных и прямолинейных движений, — именно частная (иногда говорят — специальная) теория относительности растолковывалась в предыдущих главах. 13 Это вызовет заметные неудобства: будут сильно мешать силы инерции Кориолиса — они приложены к телу, которое не неподвижно, а движется во вращающейся системе отсчета. Эти силы возникнут всякий раз, когда спортсмены станут бегать или прыгать не по линии движения стадиона (не перпендикулярно к оси карусели) — скажем, при прыжках в длину вдоль оси. Однако путем некоторых ухищрений силы Кориолиса можно свести к минимуму и пренебречь ими. 14 Надо, пожалуй, еще раз извиниться перед читателями за пренебрежение силами инерции Кориолиса. 15 Мимоходом стоит заметить, что любую поверхность можно деформировать и без изменения законов пересечения геодезических линий, а значит, без изменений метрики. Сложите тетрадный лист, скомкайте его, сверните в трубочку — во всех чертежах расстояния и углы останутся прежними. Чтобы «изнутри» отличить цилиндр от плоскости, потребуются другие соображения. Например, на цилиндре любая геодезическая (кроме образующей) замкнута — либо эллипс, либо круг. Об этой тонкости не надо забывать, но она — лишь частный случай. 16 Это не очень широкоизвестное замечание высказано советским физиком А. А. Фридманом (о его работах — после). 17 Чтобы четко понимать дальнейшее, перечитайте двенадцатую и тринадцатую главы. Кто пропустил, самое время прочитать их. |
|
|||
|
Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх |
||||
|
|
||||

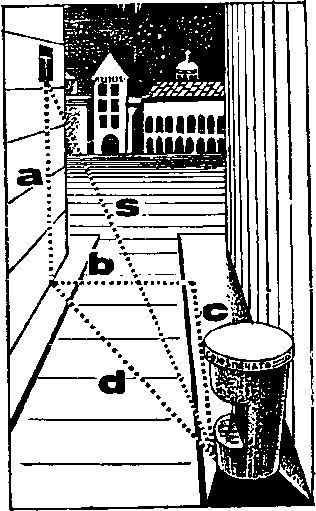 Что ж, из всего этого следует как будто немудрящий рецепт облачения пустоты в «пифагоровы штаны» и «треугольную шляпу». Надо проделать измерения длин и углов в реальных пространственных треугольниках. И таким способом «испытать пространство на кривизну».
Что ж, из всего этого следует как будто немудрящий рецепт облачения пустоты в «пифагоровы штаны» и «треугольную шляпу». Надо проделать измерения длин и углов в реальных пространственных треугольниках. И таким способом «испытать пространство на кривизну».