|
||||
|
Часть первая УДИВЛЕНИЕ ПАДЕНИЮ Глава 1. КАМЕНЬ И ПУШИНКА Через пустотуТяжесть и опасность падения — это первое, что осознает человек, освободившись от младенческих пеленок. Первый шаг, первый прыжок — и он убеждается: предстоит прожить жизнь в мире, где всегда что-то тянется к земле и падает. Освоиться с таким положением вещей помогают синяки, шишки, разбитые тарелки — словом, опыт, копящийся с юных лет. И в конце концов человек, умудренный житейским опытом, начинает думать, что он многое постиг и знает. А так ли это? Проверьте-ка себя — хотя бы на том же явлении падения. Вот вопрос. Почему камень падает? Отвечают по-разному: Потому, что он тяжелый. Потому, что его притягивает Земля. Первый ответ восходит к глубочайшей старине. Наши предки, веря своим учителям, древним мудрецам, считали, что разным телам присущи два противоположных свойства — тяжесть и легкость. И что всему на свете назначено свое «естественное» место: тяжелому — внизу, легкому — вверху. Вот и стремятся книзу камни, а дым, наоборот, поднимается. Но что такое «низ» и почему он для камня «естественнее», чем «верх», древние мудрецы не сказали.
Прошли века, и «низ» перемешался с «верхом». Очень просто: Земля оказалась шаром. Небо Австралии для нас — внизу. Но австралийские сосульки не падают на Луну, когда она оказывается «под Австралией». Что касается свойства «легкости», то его, как выяснили, не оказалось в природе. Все тела наделены тяжестью, хоть и в разной степени. Дым поднимается не потому, что он легок, а потому, что он увлекается теплым воздухом, который менее тяжел, чем окружающий холодный воздух. Так в воде всплывает пробка. Как видите, с первым вариантом ответа связано немало недоразумений и заблуждений. Второй вариант значительно моложе. Ему не более четырехсот лет. В XVI веке знаменитый астроном Иоганн Кеплер с величайшей осторожностью высказал привычную для нашего времени мысль: «Не камень стремится к Земле, а, скорее, Земля его влечет к себе». В этих словах была четко провозглашена идея земного тяготения. Предположение о таинственной силе, которая исходит от нашей планеты, пронизывает пустоту, «хватает» камень и тащит его книзу. Как будто ясно. Но чуть-чуть поразмыслите, и в этом традиционном, школьном объяснении вы найдете повод для удивления. В самом деле, почему же земное тяготение может влиять на камень через пустоту, на расстоянии? Как Земля «хватает» камень, не «дотрагиваясь» до него? Ведь то самое «действие без прикосновения», которому поразился юный Эйнштейн, разглядывавший компас, на падающем камне еще заметнее и нагляднее. Между Землей и камнем не видно никаких нитей, никаких пружин — и тем не менее происходит падение. Разве это не чудо? Нетерпеливым читателям, верно, хочется спросить: а в самом деле, почему это так? Почему Земля через пустоту тянет к себе камни и все остальные тела? Получить ответ сейчас — значит, сразу, без особых усилий, «убежать от удивления». Но столь поспешное бегство не удастся. Простой с виду вопрос на деле оборачивается труднейшей и сложнейшей научной проблемой. Гонка без победителяЧтобы понять причины чуда, нужно сперва изучить его подробности, точно разузнать, как оно происходит. Без ответа на вопрос «как» не узнаешь и почему именно так, а не иначе устроена и действует природа. Уход от всеобъемлющего почему может показаться уступкой, жертвой незнанию. Но в действительности наоборот — именно здесь шаг вперед. Это доказано всей историей науки. Итак, не почему это так, а прежде всего как это так? Сначала — как падают тела? Вот задача. Некий чудак, глазея с моста в реку, уронил кепку, решил догнать ее в воздухе и для этого сам нарочно упал с моста. Удался ли ему замысел? Сопротивление воздуха не учитывать. Вариант задачи. Что быстрее свалится со стола — дверной ключ или спичка? Какая из двух сосулек, вместе оторвавшихся от карниза, скорее достигнет тротуара — большая или маленькая? Второй (более острый) вариант. Что раньше упадет на землю, сорвавшись одновременно с одинаковой высоты (при условии отсутствия помех) —тополиная пушинка или пушечное ядро? Все эти варианты составили маленькую анкету, которую я предложил людям вполне культурным — пятерым школьникам-восьмиклассникам и трем взрослым, журналистам. Получился легонький тест на физический кругозор. Трое из опрошенных (в их числе два школьника) ответили правильно. Остальные же, те, кто начисто забыл школьную физику, уверенно заявили: чудак догонит кепку, большая сосулька обгонит маленькую, так же как ядро — пушинку. Потому что, говорили они, тяжелое должно падать быстрее легкого, так как сильнее притягивается Землей. Хорошо, когда культура человека сочетается с минимумом знаний. Увы, так бывает не всегда, что и засвидетельствовал мой тест. В действительности гонка любых тел, падающих без помех, — гонка без победителя. Уроните пушинку и ядро в безвоздушном пространстве, и вы увидите, что они полетят вниз рядышком, ни на йоту не опережая друг друга. Это касается любых тел, лишь бы не было помех падению. И это — тоже чудо. Великое чудо природы. Потому что просто невозможно поверить, не убедившись воочию, что пушинка и ядро падают одинаково быстро. Житейский опыт этого знания не дает. Больше того, он противоречит этому знанию. Нужен опыт научный — физический эксперимент. Впервые его провел, по свидетельству многих историков науки, великий итальянец Галилео Галилей. Башня в ПизеНаклонная башня в итальянском городе Пизе сейчас доставляет массу хлопот. Она наклоняется все больше и грозит вообще упасть. Итальянцы, кажется, всерьез забеспокоились и решили укрепить это уникальное архитектурное сооружение. Пока, правда, лишь разрабатываются проекты. Но надо надеяться, Пизанская башня будет спасена и сохранена. Почет башне — по заслугам. Она не только памятник зодчества. Она была чуть ли не самым первым в мире физическим прибором. И изучалось на ней то самое явление, которое ныне угрожает ее сохранности, — падение. Четыре века назад молодой профессор Пизанского университета Галилей (в ту пору еще не снискавший славы всемирно известного физика, даже не сделавший еще окончательного выбора между медициной, живописью и философией) бросал с этой башни пушечные ядра и мушкетные пули. И смотрел, как они падают. Пули и ядра падали одинаково быстро, и Галилей восхищенно удивлялся этому. Удивлялся потому, что с детских лет его учили догме: тяжелое падает быстрее легкого, и тем быстрее, чем оно тяжелее. В старых книгах это утверждение выдавалось за непререкаемую истину, ибо так заявил в свое время величайший из мыслителей древности Аристотель. Галилей осмелился кощунственно проверить и отвергнуть это мнение, призвав в свидетели природу. Так он совершил первое великое дело своей жизни, положил начало экспериментальной физике. Громкие слова эти сказаны не напрасно. Наблюдение и вывод Галилея были научным подвигом, блестящим прозрением человеческого ума, переломом в научном взгляде на мир. Тогда не принято было апеллировать к природе в решении научных задач. Считалось, что все на свете объяснимо одними лишь рассуждениями. А потому важные коллеги молодого профессора, собравшиеся внизу, у подножия башни, не желали верить своим глазам, осыпали Галилея суровыми упреками, не хотели слушать его слов. И они были отнюдь не глупцами. Нет, они были людьми просвещенными, знали древние языки, умели толковать античные тексты, разбирались в математике, находили удовольствие в философских диспутах, где изощрялись в красноречии и формальной логике. Но к естественности, к живому физическому явлению они питали надменное равнодушие. Такое уж было время — не родилась еще настоящая физика. Исследовательский ум, еще юный, незрелый, был тогда, пожалуй, слишком хвастлив. Он упивался собой и переоценивал себя. Он стыдился задавать вопросы неразумной стихии. Опыт представлялся ему занятием низким, даже жульническим. Прибегнуть к опыту значило как бы расписаться в собственной умственной слабости. Галилей тоже был сыном своей эпохи. И он не чурался витиеватой мудрости голых рассуждений. И он упражнялся в богословии. И чтил Аристотеля, ревностно его штудировал. И сперва послушно шел по его стопам. А потом сумел в нем усомниться. На такое, правда, кое-кто решался и до Галилея. Но именно Галилей первым в истории науки довел еретические антиаристотелевские раздумья о падающих телах до конкретного эксперимента. Первым сознательно решился задать вопрос природе о свойствах падения. На брюзжание пизанских коллег Галилей не уставал отвечать. По-всякому. Иногда — во вкусе оппонентов (в духе модных в те времена схоластических споров) и даже язвительными стихами. Но главное — он продолжал свои опыты. Вновь и вновь лазал на башню, старался узнать, зависит ли быстрота падения не только от веса, но и от материала, от формы тел. Этой проблеме была посвящена серия экспериментов. Круглые ядра, продолговатые пули, железные, медные — все летело с башни вниз. Экспериментировать было трудно: слишком скоро брошенные тела оказывались на земле. Вода течет в бокалЗато у себя дома в рабочем кабинете, который стал первой на нашей планете физической лабораторией, Галилей ухитрился замедлить падение. Оно стало доступно и взгляду и тщательному, неторопливому изучению. Ради этого Галилей построил длинный (в двенадцать локтей) наклонный желоб. Изнутри обил его гладкой кожей. И спускал по нему отшлифованные шары из железа, бронзы, кости. Делал, например, так. К шару, находившемуся в желобе, прикреплял нитку. Перекидывал ее через блок, а к другому ее концу подвешивал гирю, которая могла опускаться или подниматься отвесно. Гирю тянула вниз ее собственная тяжесть, а вверх, через нить, — шарик из наклонного желоба. В результате шарик и гиря двигались так, как хотел экспериментатор — вверх или вниз, быстро или медленно, смотря по наклону желоба, весу шарика и весу гири. Шарик и гиря могли, таким образом, перемещаться под действием силы тяжести. А это и было падение. Правда, не свободное, искусственно замедленное. Сперва Галилей отыскал закон устойчивого состояния этой системы: вес гири, помноженный на высоту поднятого конца наклонного желоба, должен быть равен весу шарика, помноженному на длину желоба. Так появилось условие равновесия системы — галилеевский закон наклонной плоскости. О падении и его секретах еще ничего не было сказано. Неподвижность изучать нетрудно: она постоянна во времени. Проходят секунды, минуты, часы — ничто не меняется. Весы да линейки — вот и все, что нужно для измерений[1] Затем Галилей стал изучать движение шаров. Этот- то день и был днем рождения физики (увы, календарная дата его неведома). Потому что именно тогда подвергся первому лабораторному исследованию процесс, изменяющийся во времени. Пошли в ход не только линейки, но и часы. Галилей научился отмеривать длительность событий, то есть исполнять главную операцию, присущую всякому физическому эксперименту. Поучительна легенда о лабораторных часах Галилея. В то время нельзя было купить в магазине секундомер. Даже ходиков еще не изобрели. Галилей же вышел из положения совсем особым образом. Он отсчитывал время ударами своего пульса, потом, как уверяют давние биографы, устроил неплохие лабораторные часы из неожиданных составных частей: ведра, весов и хрустального бокала. В дне ведра проделал дырочку, через которую текла ровная струйка воды. По солнцу замечал, сколько унций воды вытекало за час, и затем высчитывал вес воды, вытекающей за минуту и за секунду. И вот опыт. Ученый опускает в желоб шар и тут же подставляет под струйку бокал. Когда шар достигает заранее намеченной точки, быстро отодвигает бокал. Чем дольше катился шар, тем больше натекло воды. Ее остается поставить на весы — и время измерено. Чем не секундомер! «Мои секунды мокрые, — говорил Галилей, — но зато их можно взвешивать». Соблюдая элементарную строгость, стоит, впрочем, заметить, что эти часы не так просты, как может показаться. Вряд ли Галилей учитывал уменьшение давления (а значит, и скорости) водяной струи с понижением уровня воды в ведре. Этим можно пренебречь, лишь если ведро очень широкое, а струйка — узкая. Возможно, так оно и было. Открытие ускоренияГалилеевский рабочий кабинет — прародитель всех нынешних роскошных физических лабораторий и институтов. А потому, глядя с уважением на современные циклотроны и реакторы, не лишне вспомнить, как в старой Пизе катились по желобу шары, спускались на нитях гири, текли водяные «стрелки» часов[2]. Эта большая работа, повторенная потом в тысячах и тысячах лабораторий — научных, университетских, школьных, — была первой классической серией экспериментов с движением тел под действием тяжести. Из множества опытов Галилей отыскал главную особенность такого движения —оно равноускоренное. Чем дальше от начала пути, тем быстрее, причем скорость нарастает в равные промежутки времени строго одинаковыми порциями. Галилей первым понял, что, кроме скорости, у падающих камней и скатывающихся шаров есть еще ускорение — скорость изменения скорости. Желоб горизонтален — ускорения нет, есть только скорость. Шар катится равномерно. Появился наклон, и шар ускоряется. Круче наклонен желоб — больше ускорение. Это нехитрое понятие — замечательное открытие науки XVI века. Потому что прежде движение умели различать только по скоростям. И еще Галилей вывел формулу пути равноускоренного движения. Вот она, хорошо знакомая нашим семиклассникам S=at2/2 Путь S равен половине ускорения а, помноженной на квадрат времени t. Отличная формула! Знаешь время и ускорение — легко подсчитать путь, пройденный катящимся по желобу шаром. Знаешь путь и ускорение — вычислишь время. Знаешь время и путь — вычислишь ускорение. В том числе и таинственное ускорение силы тяжести, которое с удивительным постоянством гонит вниз падающие сосульки и пушечные ядра. В самом деле: измерь высоту Пизанской башни (S) и засеки длительность падения с нее ядра (t), а потом подставь полученные величины в нашу формулу. В аккуратном опыте ускорение силы тяжести у поверхности Земли для всех тел неизменно составляет 9,81 метра в секунду за секунду. Оно обозначается буквой g. Это то самое «же», о котором теперь так много говорят космонавты. Галилей этой цифры, правда, получить не смог. Слишком уж несовершенны были приборы. Однако было окончательно сделано важнейшее заключение: не только вес, но и материал падающего тела на быстроту его падения не влияют. Если что и замедляет падение, так это воздух (или трение о желоб). Догадка по тому времени замечательная. Лишь значительно позднее, с изобретением воздушных насосов, она была подтверждена опытом. Самоотверженный альпинистПо подсказкам Галилея мы выяснили, как падают тела: все с одним и тем же ускорением, независимо от веса и всего прочего. Но житейский опыт уверяет нас: именно вес заставляет тело падать. Если так, то получайте каверзный вопрос: тело, которое ничего не весит, и падать не должно? Верно? Давайте сообразим. И пока сделаем вид, что ничего не знаем о силе тяготения, действующей «через пустоту». Пусть вес — только давление на опору. В самом деле, вес неподвижных тел всегда проявляется как давление на опору. Камень, лежащий на моей ладони, давит на нее. Гиря давит на чашку весов. Все неподвижное весомо, если поблизости находится Земля. Убери из-под гири опору — гиря начнет падать. Почему? Хочется сказать: она начинает падать потому, что имеет вес. Не будем спорить против этого желания. Но спросим еще: а движущиеся тела — имеют они вес? Начнут они падать, если из-под них убрать опору? Попробуем разобраться логически. Альпинист, нагруженный рюкзаком, лезет на гору. Поднимается на вершину и все время ощущает вес рюкзака. При таком движении «ноша тянет». Идти с рюкзаком тяжело. Сорвешься с горной тропки — полетишь в пропасть. Ну, а каково с рюкзаком падать, тяжело или легко? Или, скажем, такой вопрос: с каким рюкзаком легче падать, с тяжелым или легким? Сохранится вес у падающего рюкзака? И у падающего альпиниста? Ради опыта альпинист самоотверженно спрыгивает с горы. Низвергается вниз. Но... если альпинист и его рюкзак сохранят в падении свой вес (как давление на опору), то выйдет несуразица. Судите сами. Альпинист летит вниз, а рюкзак, раз он сохраняет вес и, значит, давит на альпиниста сверху, подгоняет его падение. Без рюкзака он падал бы медленнее. Тяжелее рюкзак — вроде бы быстрее падение. С другой стороны, и один рюкзак без альпиниста падал бы медленнее, потому что альпинист не тянул бы его своим (сохранившимся) весом снизу. А привязав к себе медленно падающий рюкзак, альпинист замедлил бы, словно парашютом, и собственное падение. Выходит, тяжелее рюкзак — медленнее падение. Вот и несуразица: если в падении тела сохраняют вес, то, надев рюкзак, альпинист должен падать одновременно и быстрее и медленнее, чем без рюкзака. Такого быть не может, это — противоречие, чепуха. Вывод: надетый рюкзак во время падения, во-первых, не давит на альпиниста и, во-вторых, не тянет его вверх. Другими словами, падающий рюкзак ничего не весит. И альпинист тоже ничего не весит, когда падает. У человека, свалившегося с горы вместе с поклажей, «ноша не тянет». Для всех без исключения свободно падающих тел тяжести не существует. Они пребывают в состоянии невесомости. Странный получился вывод. Тяжесть — причина падения, а все, что падает, не имеет этой самой тяжести, невесомо. Для новичка это неожиданно и удивительно. Но если вдуматься, вывод логичен[3]. Он отлично согласуется с тем, что мы узнали раньше о постоянстве земного ускорения. В свободном падении нет тяжести (именно как давления на опору). Падающие песчинка и мельничный жернов не давят друг на друга — летят рядом в полном равноправии, в каждый момент с одинаковой скоростью, с одинаковым ускорением g. Кто прав, кто виноватИтак, вес, как давление на опору, отнюдь не прикован к телу навечно. Его нет у тел, которые свободно падают. Узнав это, давайте-ка рискнем ответить на манящее «почему»: почему все тела падают одинаково быстро, с равным ускорением? Попробуем сказать: потому что в падении они теряют вес, а это делает невозможным падение с разными ускорениями (во избежание чепухи, с которой мы столкнулись, когда рассуждали об альпинисте и его рюкзаке). Если хотите, можете перевернуть вопрос. Спросить: почему падающие тела теряют вес? И ответить: потому что они падают с одинаковым ускорением (стало быть, не могут давить друг на друга). Удовлетворены вы? Едва ли. Это ведь что-то вроде слов «потому что потому», глубокомысленно сказанных в ответ на «почему».  Пропажа веса — важный признак падения, но, подметив этот признак, мы еще не нашли его причины. Как не нашли мы и причины одинакового ускорения всех свободно падающих тел. Приведенные ответы ничего не объясняют, только сваливают вину с больной головы на здоровую. Ускорение падения постоянно — виновата-де потеря веса. Вес падающего тела пропал — надо винить постоянство ускорения в падении. А тут правых и виноватых искать бессмысленно. Падающие тела пунктуально исполняют законы природы. Значит, я рано попытался отвечать на «почему». Удивление разрешить пока не удалось. Столь же таинственным осталось и наше главное удивление — тому, что Земля действует на камень через пустоту, без всякого прикосновения. Глава 2. ЧТО ТАКОЕ ИНЕРЦИЯ Куда залетит копьеЧерез двадцать строк вас ждет сообщение еще об одном чуде природы. Чтобы легче понять его, сделаем физкультурную разминку — займемся метанием копья. Я разбежался по зеленому полю стадиона, сосредоточил волю в резком броске — и копье летит вперед. Дальше, выше!.. Ниже... Упало. Далеко оно пролетело? Для нашей космической эры — не очень. Если метров на 100, значит, я мировой рекордсмен. А хорошо бы закинуть копье прочь от стадиона, километров этак за сто, за тысячу, вообще куда-нибудь в бездну Вселенной. Как вы думаете, много силы надо иметь для этого? Да почти совсем не надо. Любой ребенок способен на такое, если только он предварительно уберет с дороги помехи движению копья. Главных помех немного — всего две. Первая — Земля. Она влечет к себе брошенное копье (так сказал бы Кеплер) и заставляет его в конце концов упасть. Вторая помеха — воздух, который тормозит копье. Вот и все. Уничтожьте Землю и воздух — и от малейшего толчка ваше копье улетит куда угодно. Здесь мы и столкнулись с очередным чудом природы. Для неискушенного в физике человека оно, пожалуй, еще удивительнее, чем чудеса тяготения, действующего через пустоту, и одинаковой ускоренности падающих тел. Ведь загадка тяготения видна сразу, постоянство земного ускорения легко заметить по упавшим с карниза сосулькам. А неуничтожимость начатого движения никак не увидишь: все в нашем мире, где невозможно «убрать с дороги» Землю и воздух, тормозится и падает. Древние мудрецы думали поэтому, что движение брошенного камня происходит потому, что его проталкивает вперед воздух, окружающая среда. Так же, как удав проталкивает проглоченного кролика.  Хитро? Не очень. При таком объяснении совсем непонятно, почему же копье, летящее в воздухе, тормозится. В действительности разогнанное копье летит само, если не встречает помех, летит, ничем не подталкиваемое, как угодно далеко — по прямой линии, с постоянной скоростью. Но все-таки почему бы копью, летящему в пустоте вдалеке от планет и звезд, не остановиться вдруг или, наоборот, разогнаться, свернуть по дуге, завертеться по какой-нибудь спирали, кувыркнуться? Что заставляет его держаться прямого пути, сохранять скорость? Постепенно сложилось такое мнение. Копью, как и любому другому физическому телу, присуще свойство инерции, которое и олицетворяет это универсальное стремление всех тел к сохранению покоя или равномерного прямого движения. Копью «все равно», покоится оно или движется. Оба состояния для него равноценны. И благодаря своей инерции оно бережно хранит каждое. В фразах, которые вы только что прочитали, изложен знаменитый закон инерции. О нем догадывались многие мыслители — и гениально многогранный Леонардо да Винчи, и Галилей, и французский философ Рене Декарт. Но только великий английский ученый Исаак Ньютон до конца понял его значение, назвал его первым законом механики и поставил в основу этой области физического знания. В конце главы мы к этому закону еще вернемся. А потом и в конце книжки. Сложение нулейНадеюсь, вы не в претензии, что я обращаюсь с Землей, как футболист с мячом: захотел и отбросил ее, чтобы «не мешала». Ради удобства рассуждений и наглядности ученые нередко устраивают подобные «мысленные эксперименты». Значит, и нам с вами они не запрещены. Итак, мы откинули Землю вместе с ее любопытным умением придавать вес всему, что пребывает рядом. Поэтому наше летящее по инерции копье не будет ничего весить: тяжести-то неоткуда взяться, нет того, что заставляло бы наше копье давить на опору. Вес тела вдали от Земли, если верить Кеплеру, равен нулю. Ну, а если мы теперь вернем Землю и поставим ее где-нибудь подле летящего копья так, чтобы оно попало в зону земного притяжения, — приобретет тогда наше копье вес? Новичка тянет сказать: да, приобретет. А на самом деле — нет. Как только Земля водворена на место, копье начнет на нее падать — двигаться в направлении ее центра. Кроме того, оно будет продолжать по инерции лететь вперед, ибо появление Земли не сможет отменить первоначальный толчок, в свое время пославший копье по прямому пути. Получается совмещение двух движений. Копье будет сразу и лететь вперед (прямо и с постоянной скоростью) и отвесно падать в направлении к Земле (с ускорением свободного падения). В первом движении вес копья равен нулю. Во втором движении, которое только и добавилось из-за возвращения Земли, вес копья тоже равен нулю, ибо падающие тела не имеют тяжести. Займемся сложением: нуль плюс нуль равно нулю. Вывод: несмотря на возвращение Земли, свободно брошенное копье продолжает оставаться невесомым. Падает вверхНеожиданное известие: не только прославленные космонавты, но и остальные люди, в том числе читатели этой книжки (как и всех остальных), некоторую часть своей жизни проводят в состоянии невесомости. Удивились? Очень хорошо. Пусть Земля где-то в стороне. Копье брошено и летит в определенном направлении, например вправо, точно по строке, которую вы сейчас читаете. Берем в руки Землю и помещаем ее перед летящим копьем — так, чтобы центр планеты находился на прямой линии, продолжающей вправо ту же строку. Что произойдет с копьем? Направление его движения не изменится. Путь останется таким же прямым, как и без Земли. Только из равномерного полет превратится в ускоренный. Получится нечто вроде обыкновенного отвесного падения, но с большей начальной скоростью, а потому более быстрое, хоть и с прежним ускорением. И, разумеется, копье останется невесомым (ибо, напоминаю, складывая нули, получаем нуль). Случай второй. Подносим Землю с противоположной стороны — помещаем ее центр слева от копья на прежней линии. Теперь копье сперва будет лететь, как и раньше, вперед (от Земли), но не равномерно, а замедленно (потому что Земля тянет его назад), потом замедлится настолько, что на мгновение остановится (в этот момент полностью исчезнет скорость, сообщенная копью первоначальным толчком), и тут же двинется назад, к Земле, в обычном отвесном падении. Опять, по известной вам причине, копье останется невесомым, несмотря на то что некоторое время оно двигалось не к Земле, а от Земли — падало вверх! — и на бесконечно малое мгновение останавливалось, когда меняло направление. Гагарин или Брумель?Перекидка планеты вовсе не обязательна. И не трогая ее, можно прийти к тем же заключениям. Вы стоите на стадионе и бросаете вверх все то же копье, если оно вам еще не надоело. Во время взмаха оно ускоряется, а вылетев из рук, участвует сразу в двух движениях: равномерном, направленном вверх (точно таком же, как если бы не было Земли), и ускоренном, направленном вниз — отвесном падении. Тут тяготение включается не с запозданием (что мы делали раньше из соображений наглядности), а сразу после разгона. Результат же прежний: едва копье вырвалось из ваших рук, оно потеряло вес. Если, конечно, пренебречь сопротивлением воздуха. Можно закинуть копье не вверх, а куда-нибудь вбок, под углом к вертикали — опять после толчка будет сложение прямолинейного равномерного движения по инерции с отвесным падением. Значит, исчезнет тяжесть. Только на этот раз искривится путь. Многим кажется странным, что брошенный камень теряет вес тотчас после вылета из руки. Легче согласиться, что он невесом во время движения вниз. Но интуиция подводит. И вверх и вниз брошенное тело летит, не имея ни грамма веса. Все, что вы подбрасываете — камни, палки, пятаки, мячи, самих себя (когда прыгаете), — после броска пребывает в свободном падении и потому невесомо (разумеется, до тех пор, пока можно не считаться с сопротивлением воздуха). И поскольку прыжки случаются довольно часто в вашей жизни (я уж не говорю о бесконечных падениях, особенно в младенческом возрасте), эту часть жизни вы находитесь в состоянии невесомости. По той же причине Валерий Брумель, я думаю, был в невесомости больше, чем Юрий Гагарин. Если Брумель ежедневно совершал десять тренировочных прыжков длительностью по полторы секунды каждый (это соответствует двухметровой высоте прыжка), то за десять лет (за вычетом воскресений) он был в невесомости примерно пятнадцать часов. Это почти в десять раз дольше орбитального полета корабля «Восток». Впрочем, и Гагарин спортсмен. И он прыгал, бегал, упражнялся на батуте. К тому же он старше Брумеля. Так что, возможно, Гагарин и тут первый. Опровергаем фантастовНе стоит в сотый раз журить за ошибку Жюля Верна, который в романе «Из пушки на Луну» уверял, что невесомость в снаряде наступит где-то в середине пути между Землей и Луной (когда-де уравновесятся притяжения Земли и Луны). Теперь вину приписывают ученому-консультанту знаменитого фантаста: консультант- то обязан был знать, что на самом деле невесомость должна была наступить тотчас по вылете снаряда из жерла пушки. Но, видимо, по этому примеру, а также и по собственной инициативе писатели-фантасты сочинили затем массу небылиц про невесомость. Например, «падая на чужую планету, звездолетчики всем своим существом чувствовали ее могучее тяготение». Или «двигатели умолкли, ракета удалялась от Земли, и постепенно все вещи становились легче». Объясните сами, почему это неверно. Даже теперь, в разгар космической эры, про невесомость то и дело говорят опрометчивые вещи. Многие ваши друзья, читатель, считают, что наши космонавты были невесомы потому, что оказались далеко от Земли. Ручаюсь, что по крайней мере человек шесть из десяти думают в таком роде (сам проверял!). В действительности и космонавты в своих кораблях-спутниках падали. Ракета-носитель настолько сильно разогнала корабль-спутник, что когда он был отпущен ракетой и перешел в свободное падение, то, сворачиваемый к Земле тяготением, не успевал упасть на нее. Движение корабля по инерции, направленное всегда вперед вдоль касательной к криволинейной орбите, было очень быстрым — около восьми километров в секунду. Вот и кружился корабль вокруг планеты, совершая виток за витком. Падал и не мог упасть! Алексей Леонов, который выбрался из корабля в космос, тоже падал и не мог упасть. В космосе он даже не отстал от корабля и не опередил его по той же самой причине, по которой маленькая сосулька не отстала в падении от большой и не опередила ее. Будь скорость космического корабля больше одиннадцати километров в секунду, он, падая, улетел бы прочь от Земли. При шестнадцати километрах в секунду ушел бы даже из Солнечной системы!  Ванна невесомости Теперь вы можете без всяких хлопот исполнить старый замысел Уэллса — избавить человека от веса. Если под руками нет космической ракеты и корабля-спутника, надо попросить человека подпрыгнуть, только и всего. Так, правда, он освободится от тяжести ненадолго. Лучше посадить его в самолет и попросить пилота, чтобы тот забрался повыше, разогнался вверх и резко снизил тягу двигателей — чтобы она преодолевала только сопротивление воздуха. В этом режиме самолет полетит по «баллистической кривой» — сначала поднимется с замедлением, а потом будет ускоренно опускаться. Движение самолета будет таким, как если бы у Земли отсутствовала атмосфера. Произойдет полная имитация свободного падения в безвоздушной среде. Если самолет высотный и достаточно быстроходный, а летчик опытный, каждый баллистический прыжок продлится довольно долго — минуту, а то и больше. Именно таким способом проходят тренировку космонавты, чтобы подготовиться к многодневной невесомости космического полета. В самолетах устраивают «ванны невесомости» — просторные кабины, где удобно парить в воздухе, кувыркаться, отталкиваясь от мягких стенок, в критических случаях хвататься за поручни — и все это без риска с непривычки натворить бед на каком-нибудь пульте. Ванну эту я сейчас использую, с вашего разрешения, не по прямому назначению: пусть она побудет боксерским рингом. Зачем боксеру вес?Какой-нибудь рекордсмен-сверхтяжеловес, позабывший чудесные школьные годы, наверное, обидится на этот вопрос. Он убежден, что вес ему совершенно необходим— чтобы тяжелыми были кулаки, весомыми удары. Предложите этому боксеру лишиться веса, и он, я думаю, пошлет вас в нокдаун. Все же проявите такт и постарайтесь зазвать в ванну невесомости даже не одного спортсмена, а двух, да еще разных весовых категорий. Если вам это удастся, сделайте эксперимент — упросите боксеров, ради интересов научной популяризации, провести небольшой показательный бой. Достаточно одного раунда. И вот в ванне невесомости дерутся два боксера, тяжеловес и легковес. Лучше сказать, бывший тяжеловес и бывший легковес. Теперь они оба «ничегоневесы», ибо вес каждого равен нулю. Казалось бы, весовые категории спортсменов выравнены, шансы на победу одинаковые. Но присмотримся к бою. Довольно быстро боксеры освоились с необычной обстановкой. Им уже не мешает отсутствие верха и низа, невозможность опираться на ноги. Опытные спортсмены применились к невесомости и азартно дерутся. Бывший легковес подвижен и быстр. Так и сыплет свингами по неповоротливому и спокойному бывшему тяжеловесу. Тот не спешит. Удары его неторопливы. Но какой эффект от каждого! Боковой крюк — и легковес (бывший) завертелся, как волчок. Могучий апперкот — и бывший легковес мчится к потолку, отскакивает от него мячиком. Бывший тяжеловес, несмотря на свою невесомость, буквально давит бывшего легковеса. И за его явным преимуществом вы, не дождавшись конца раунда, прекращаете бой. Хватит. Бокс — не уличная драка. Даже во имя науки не следует допускать избиения людей. Разбор поединкаПроизошло доказательство того, что вес боксеру совсем не обязателен. Бывший тяжеловес победил, сбросив все свои килограммы! Почему же? Может быть, у победителя лучше развиты мышцы? Это нетрудно проверить. После боя, отходив обессилевшего легковеса (а лучше, разумеется, до боя, чтобы оба спортсмена были свежими), вы даете им по эспандеру — пусть посоревнуются в растягивании тугой резины. И выясняется, что оба они могут растянуть эспандер одинаковое число раз. Значит, мышцы у них развиты одинаково. Ради строгости допустим, что, кроме того, вы проверили быстроту их спортивной реакции, стратегические навыки, тактические приемы, опыт, даже, если хотите, умственные способности. Во избежание придирок, оговоримся еще одним невероятным условием: наши боксеры дрались в рыцарских латах и поэтому с одинаковой болезненностью переносили удары равной силы (дабы не давать легковесу преимущества, известного по стихотворной строке из «Василия Теркина»: «Хорошо, что легок телом, отлетел, а то б конец...»).  Так, буквально все качества боксеров, кроме веса, оказались как будто одинаковыми. А во время боя равным — нулевым — был и вес. В чем же, в конце концов, было преимущество бывшего тяжеловеса? Его преимущество — в инерции, в том самом свойстве сохранять покой или прямолинейное равномерное движение, которое положено Ньютоном в основу механики. Инерция ведь у разных тел разная. Больше инерция — значит, тело медленнее реагирует на толчок или напор, а если уж движется, то крепко держит скорость и быстрее рушит преграды. Об этом и свидетельствовала картина боксерского боя. Бывший тяжеловес посылал удары, от которых бывший легковес вертелся, кувыркался и отскакивал. Наоборот, от весьма сильных наскоков бывшего легковеса противник только слегка покачивался. После боя нельзя было сказать традиционное «победил сильнейший» (оба одинаково сильны). В невесомости не годились и слова «победил тяжелейший». Надо было объявить: «Победил инерционнейший». Разумеется, печальный исход поединка можно было предотвратить, если бы вы не ограничились лишением боксеров веса, а еще и заранее учли инерцию каждого из них. Можно было измерить инерцию до боя? Можно. А как? Как вообще измерить инерцию? Поставлен вопрос, который имеет в физике исключительную важность. Перед ответом — еще одно замечание. Оно хоть и не ново для внимательных читателей, но должно их немножко запутать, сбить с толку и вместе с тем дать верное направление мысли. Вот какое замечание. Инерция действует всюду, в любых условиях, в любых состояниях. Она неотделима от тела — будь то сосулька, дождевая капля или целая планета. Она — не то, что вес, который может быть, а может и не быть. Потому что невесомое тело тоже обладает инерцией — недаром мы уничтожали Землю вместе с ее тяготением, когда швыряли в космос копье, полетевшее затем по инерции, или устраивали поединок невесомых боксеров, в котором победил инерционнейший. Это замечание и должно вас запутать. И вот почему. В кажущемся противоречии с тем, что сейчас было сказано, инерцию тела проще всего определить с помощью взвешивания. Что нужно охотникуВ магазин приходит охотник и просит отвесить ему пять килограммов дроби. Какое физическое свойство он покупает? Инерцию. Инерционный полет выстреленных дробинок — вот что ему требуется. Ведь благодаря инерции, стремлению сохранить равномерное прямолинейное движение летящие дробинки погубят утку, которая на них неосторожно наткнется. Заметьте: охотнику совсем не нужен вес дробинок. Охотник рад купить невесомую, но достаточно инерционную дробь — легче было бы шагать по лесу. Если бы можно было охотиться в далеком космосе (на каких-нибудь живых комет, придуманных фантастами), перед выходом на охоту космонавты запасались бы именно невесомыми дробинками или пулями. Но дробь продается на вес. Ибо вот непреложное правило: если уж тело имеет тяжесть, то в одинаковых условиях взвешивания она тем больше, чем больше инерционность, присущая телу. Здесь прямая пропорциональность. Давным-давно об этом знают и охотники, и артиллеристы, и продавцы в охотничьих магазинах. И, конечно, физики. Поэтому исход боя наших невесомых боксеров был предрешен заранее: тяжеловес на Земле инерционнее легковеса и остается таким же в ванне невесомости. На случай, если вам придется судить боксерские встречи в межпланетных полетах, запомните: весовые категории спортсменов следует сохранить, но лучше переименовать их в категории инерционности. Да и на Земле их вернее называть именно так. Все сказанное, однако, не значит, что единицами веса можно измерять инерцию. Килограммы веса не годятся на эту должность по той же старой причине: они «прогульщики». Пока дробинки в магазине или в охотничьем патронташе — они весят, а после выстрела — невесомы. Как же быть? Кого взять на вакантную должность? Что нужно домашним хозяйкамИнерцию покупают не часто. Редко приобретают в чистом виде и вес — это делают, например, спортсмены-тяжелоатлеты, когда обзаводятся гирями, гантелями и штангами. Толпы людей, снующих ежедневно по магазинам, не интересуются ни весом, ни инерцией. Ну зачем вам, скажем, инерционность яблока? Чтобы швырнуть его и разбить чье-то окно? Никчемное занятие! Домашние хозяйки, как и охотники, страдающие от тяжести дроби, с удовольствием лишили бы веса свои сумки, набитые снедью. В булках и колбасах, пачках сахара и пакетах крупы нас интересует не тяжесть, а количество вещества. Ибо десятком невесомых сосисок можно отлично позавтракать в кабине космического корабля. Количество вещества в физике называют массой. Лучше сказать: чем больше в теле вещества, тем больше его масса. И по тысячелетнему опыту тружеников прилавка, подтвержденному физиками, массу можно измерять по «бесплатному приложению» — весу. Потому-то во всех продуктовых магазинах стоят весы. Причем тут, как и при взвешивании инерционности, прямая пропорциональность: во сколько раз больше масса тела, во столько раз больше и его вес (разумеется, опять-таки при равных условиях взвешивания). Тело тем больше давит на опору, чем больше в нем вещества, чем больше его масса. Но, в отличие от веса, масса не «прогульщица». Она всегда при теле: и на Земле, и в космосе, при любом движении. В том числе и во время свободного падения, когда тело невесомо. Так же, как инерция. Отсюда вывод: именно количество вещества, массу, можно принять на вакантную должность меры инерции. И в единицах массы измерять инерционную способность тел. Лебедь и щукаНе будем спешить. Позволим себе воспоминания и повторения. Отыскана мера для измерения инерции — количество вещества, масса. Количество вещества, значит, замедляет разгон и торможение тела. Но обратите внимание: то же самое количество вещества, та же самая масса, весит. Будучи неподвижной и находясь вблизи Земли, давит на опору. А когда опору убирают, начинает падать.  Вот только сейчас, после подготовки, содержащейся на предыдущих страницах, я рискну наконец назвать вес «по-школьному» — силой тяготения. Так, как вслед за Кеплером учил Ньютон. А в связи с этим пришла пора разъяснить, что именно Ньютон понимал под термином сила. В физике сила есть всегда результат взаимодействия тел, их влияние друг на друга, то, что нарушает покой или равномерное прямолинейное движение взаимодействующих тел, сообщает им ускорение. Сила тяготения — влияние Земли на камень. Таинственное влияние, которое Ньютон назвал дальнодействием, потому что оно происходит без контакта, «через пустоту». Даже если камня вблизи Земли нет, там есть нечто, что подействовало бы на камень, будь он там. Это нечто, посредством которого Земля «через пустоту» влияет на камень, именуют гравитационным полем или полем тяготения. По какому закону дальнодействующая сила тяготения действует на тело — об этом пойдет речь в следующей главе. А сейчас отметим лишь то, что эта сила приложена к веществу тела, к его массе. Именно за массу «хватает» Земля «через пустоту» камень или копье и заставляет их падать, тянет к себе, ускоряет. Такова точка зрения Ньютона. Еще раз. Действуя на сосульку, сорвавшуюся с карниза, земное притяжение ее разгоняет. Массе присуще ускорение в поле тяжести. Но, кроме того, она же, эта же самая масса, благодаря своей инерционности, противится ускорению, замедляет разгон сосульки. Вот вам замечательное противоречие, заложенное не в человеческих рассуждениях, а в самой сути природы! Прочувствуйте его хорошенько. Можно условиться в следующем (физики так и делают): в одном и том же теле уживаются две разные массы, наделенные противоположными свойствами. Та, что «слушается» силу тяготения, ускоряется к Земле, называется тяжелой массой. Или гравитационной. А та, что «не желает» поддаваться силе, «старается» сохранить покой или равномерное прямолинейное движение, уменьшает поэтому разгон, — инертной, инерционной. Сосулька падает — и в ней непрерывно конкурируют противоположные стремления: ускоряться и не ускоряться. В одном возу из старой крыловской басни спрятались невидимый лебедь и невидимая щука — вот, если хотите, сравнение (не очень верное, правда, — это скоро выяснится). Во всяком случае, теперь ясно, что делать дальше. Надо разгадать «спор» двух масс. Тогда, надо надеяться, будет понятней и само явление падения сосульки. Сила побеждаетВ басне о раке, лебеде и щуке «воз и ныне там». Он неподвижен, потому что к нему приложены силы, уравновешивающие друг друга. У нас — иное. Отличие не только в том, что отсутствует «рак», это не так уж важно. Наш «воз» не неподвижен, несмотря на старания «лебедя» (инерции), он падает вниз — туда, куда его тянет «щука» (сила тяготения). Значит ли это, что тяжелая масса больше инертной? Нет. Инерция — не сила (хоть и существуют так называемые силы инерции — о них будет сказано немного позже). Сравнивать инерцию с лебедем, строго говоря, нельзя, ибо настоящий лебедь, который «рвется в облака», прикладывает к настоящему возу именно силу — то, что изменяет скорость воза, придает ему ускорение. Инерция же — это пассивное «непослушание» силе. Дабы не запутаться в словах, применим математические символы. С их помощью все сказанное записывается коротко и наглядно во втором законе механики: ускорение тела (а) прямо пропорционально приложенной силе (F) и обратно пропорционально инерции, то есть инертной массе тела. Вот формула: a=F/mi Из нее, в частности, следует, что лишь в предельном случае — при бесконечно большой инертной массе — ускорение равно нулю. А когда инертная масса хоть и велика, но конечна, то даже под ничтожным напором тело пусть очень медленно, но разгоняется. Сила побеждает любую инерцию. Активное начало держит верх над пассивностью. И поэтому все, что имеет массу, должно падать. Внимание! Мы, кажется, близки к ньютоновской (классической) разгадке одного из чудес падения. В сосульках и пылинках, песчинках и жерновах непрерывно «спорят» две массы: тяжелая и инертная. И хоть самому факту падения этот спор не мешает (сила тяготения всегда побеждает и сдвигает тело с места), но именно тяжелая и инертная массы определяют исход гонки падающих тел. Спор массКак же они соотносятся, эти две массы, какая из них все-таки больше? Теперь сообразить нетрудно. Пусть больше тяжелая масса. Тогда она «переспорила» бы соседку и тяжелые тела лучше «слушались» бы силу, чем «упрямились», — падали бы быстрее легких. Падающий жернов обогнал, бы падающую песчинку. Но с первых страниц этой книжки мы отлично помним, что это не так. Пусть больше инертная масса. Тогда, наоборот, легкие тела падали бы быстрее тяжелых. Песчинка обогнала бы жернов. Однако и этого не наблюдается в природе. Гонка падающих тел не имеет победителя. Единственно возможный вывод: массы-соседки не могут друг друга «переспорить», а потому тяжелая масса равна инертной. Всегда равна, в любых условиях. Чтобы до конца соблюсти точность, надо сказать, что во всяком случае обе массы пропорциональны: во сколько раз возрастает одна, во столько увеличивается и другая, а при соответствующем выборе единиц измерения пропорциональность становится равенством. И в результате падающие тела падают так, как увидел Галилей: с постоянным ускорением, не зависящим от массы. Вот она, как будто, причина чуда, которую мы так долго искали! Равенство тяжелой и инертной масс! Можно поставить множество тонких опытов для проверки этого заключения. Тут не только свободное падение тел. Всевозможные маятники, балансы, крутильные весы, вариометры позволяют скрупулезнейшим образом экспериментально измерить обе массы. В начале нашего века многочисленные опыты такого рода исполнил венгерский физик Роланд Этвеш. В тончайшем приборе, который изобрел Этвеш, и в других, более поздних, равенство тяжелой и инертной масс было подтверждено вплоть до одиннадцатого знака после запятой. Даже в стомиллионных долях процента оно оказалось безупречным! Вне всякой зависимости от химического состава, плотности, состояния тел. Именно поэтому жернов и пушинка падают в пустоте одинаково быстро. Именно поэтому они в падении ничего не весят. Хочется свободно вздохнуть и сделать перерыв в бегстве от нашего удивления. С тем, однако, чтобы после перерыва выставить еще одно «почему»: почему же тяжелая масса равна инертной? В самом деле, почему? Что это за странное равенство? Тут ньютоновская механика молчит. Ответа не знает. Ответ лежит за ее пределами, куда мы в свое время заглянем. И в конце концов окажется, что существует совсем иной, гораздо более простой (с точки зрения «устройства природы», хоть и гораздо более сложный для понимания) способ объяснения загадки падения. Способ, обходящийся без разговоров о делении массы на тяжелую и инертную, даже без истолкования веса как дальнодействующей, мгновенно проникающей «через пустоту» силы тяготения... Поскольку сразу постичь все это невозможно, примиритесь с постепенностью познания. Еще долго мы не покинем ньютоновских владений, где нас ждет немало поучительного и многозначительного. Глава 3. ЧТО ТАКОЕ ДВИЖЕНИЕ Закон-пословицаШирокой публике лучше других знаком третий закон механики. Он так хорошо известен, что стал новой пословицей. Ньютоновскую формулировку: «Всякое действие имеет равное и противоположно направленное противодействие» — сейчас употребляют, мне кажется, чаще, чем старую: «Как аукнется — так и откликнется». Смысл схож, только первое выражение определеннее и точнее. Правда, непосвященные чаще изрекают эту сентенцию по поводу событий бытовых или уличных — всякого рода склок и потасовок, и там, пожалуй, действие далеко не всегда равно противодействию. Если же речь идет о физике, то закон должен быть проверен экспериментально и соблюдаться всегда. Для проверки Ньютон собственноручно поставил несколько опытов. Вот один из них. На дощечке, плавающей в воде, лежат магнитная подковка и кусочек железа. Всем известно, что магнитом железо притягивается. А железом притягивается магнит? Да, притягивается — это следует из простейшего опыта. Итак, магнит и железо на дощечке, притянувшись, толкают друг друга в разные стороны. Что толкает сильнее? Если магнит, то дощечка поплывет, разгоняясь, в направлении линии, проведенной от магнита к железу и дальше. Если сильнее толкает железо, дощечка тронется, получив ускорение в обратную сторону. В обоих этих случаях действие магнита на железо не будет равно противодействию железа на магнит. Ньютон убедился: дощечка, нагруженная притянувшимися магнитом и железом, либо недвижима, если она покоилась, либо плывет равномерно по прямой, если она раньше двигалась. Значит, третий закон верен: действие в точности равно противодействию. Вместо плавающей дощечки можно вообразить Землю в мировом пространстве. Если бы взаимное тяготение разных ее частей не уравновешивалось, планета унеслась бы в бесконечность, непрерывно ускоряя самое себя. Вы вправе еще представить, что величайший силач, потерявший весла, пытается сдвинуть лодку давлением изнутри на ее нос. В лучшем случае он не сломает лодку, которая ни на миллиметр не продвинется вперед. По той же причине барон Мюнхаузен не сможет поднять себя за волосы. Вездесущая реактивностьА что случится, если силач сломает лодку или Мюнхаузен, переусердствовав, оторвет себе голову? Во исполнение третьего закона произойдет отдача, то самое, что толкает приклад выстрелившего ружья в плечо охотника и движет космическую ракету. Когда оторванный нос лодки ринется вперед, корма ее отскочит назад. Выбрасывая мощный поток раскаленных газов, реактивный двигатель поднимает и разгоняет космический корабль. И не только космический. «ТУ-104» — это атмосферный реактивный самолет. Его двигатель схож с ракетным. Но вот это любопытно. Не только он, но и все прочие самолеты, в том числе и винтовые, тоже, строго говоря, реактивные. Да и автомобили, паровозы, пароходы, велосипеды, брички, дилижансы, пешеходы опять-таки реактивны. Таковы, по сути дела, почти все окружающие нас движения. Все, которые подчинены третьему закону Ньютона и обязаны ему своим существованием. Ракета отличается лишь тем, что сама готовит реактивное «рабочее тело» — раскаленные газы, которые она выбрасывает прочь и противодействие которых ее движет в обратную сторону. А для винтового самолета, автомобиля, парохода реактивное «рабочее тело» уже готово — воздух, дорога, вода. «Отбрасывая» их назад, экипаж движется вперед. Действует третий закон. Я иду по планете потому, что своими ногами толкаю ее назад. Планета, правда, не спешит разгоняться в обратную сторону. Потому что обладает колоссальной массой. Будь на моем месте белка, а на месте планеты колесо, реактивность движения стала бы очень заметна — масса колеса сравнительно невелика, а значит, и его инерционность. Третий закон Ньютона, как видите, проявляет свое действие очень широко. Однако лишь до тех пор, пока на сцену не выходят силы инерции — то единственное в механике, что ему не подчинено, действия этих сил не сопровождаются противодействиями. Почему это происходит, вы узнаете чуть позже. Предварительно несколько существенных замечаний. По ПушкинуЧитатель уже вобрал в свою голову столько премудрости, что я задам ему сейчас глубочайший философский и физический вопрос: что есть движение? В самом деле, что? Мы все время говорим «движется», а понимаем ли, что значит это слово? У Пушкина:
Иначе (и длиннее) говоря, мудрец стал с течением времени менять свое пространственное положение по отношению к «брадатому» коллеге. Этим было без слов сказано все. Этим была определена сущность механического движения — именно так, как она понимается в физике. Запомните: движение есть изменение с течением времени положения тела в какой-либо системе отсчета. Последние слова совершенно обязательны. Очень важно четко представить себе: без системы отсчета пространства и времени движения не существует. Для «брадатого мудреца» системой отсчета служила, видимо, скамья и земля, на которой он сидел, плюс удары его сердца, игравшие роль часов. В этой системе второй мудрец менял свое положение. А значит, двигался. Ничего иного в понятие механического движения физик не вкладывает. Система отсчета — это некая материальная основа для измерения расстояний и длительностей. Скажем, набор скрепленных линеек, угломерных инструментов, часов. Даже если их нет, их всегда можно домыслить, вообразить, когда речь идет о движении. Так мы и делали раньше, рассуждая о падающих камнях и летящих копьях. Так будем делать и впредь — и часто с большей определенностью и конкретностью. Сказанное сейчас дает пищу для сложных и глубоких раздумий. Мы займемся ими позже, в следующих частях этой книжки. Но самые существенные особенности систем отсчета, их связь с законами движения надо отметить сразу. Инерциальность и неинерциальностьПредставьте себе огромную кастрюлю, парящую где-то в космосе далеко от планет и звезд. Может быть, это внутренняя полость фантастической «летающей тарелки». Иллюминаторы задраены. Нет никаких возможностей посмотреть изнутри на небо, увидеть усыпанную звездами небесную сферу. Вы внутри этой кастрюли. Обутые в башмаки с намагниченными подошвами, шагаете по жестяному дну. И имеете следующее научное задание: установить ускорение либо вращение кастрюли или доказать, что то и другое отсутствует. Поразмыслив, вы, я думаю, решите заданную задачу. Можно сделать, например, так: нарисовать на дне идеальную прямую (скажем, с помощью светового луча) и бросить вдоль нее копье. Так вот, если копье, летя по инерции, будет с неизменной скоростью точно следовать нарисованной прямой линии, наша кастрюля не вращается и не испытывает ускорений. Если же брошенное копье куда-то свернет от прямой, закружит, разгонится или затормозится, резонно заключить, что «на самом деле» вращается и ускоряется кастрюля. Логика умозаключений тут основывается на первом законе механики, на признании инерции. Выводы выглядят вполне разумными (до некоторого предела, впрочем, который в своем месте — еще очень не скоро — будет отмечен). И здесь четко проступает роль системы отсчета в изучении движения. Теперь важное определение. Постарайтесь его запомнить. Кастрюля, которая после опыта с копьем выглядит невращающейся и неускоряющейся, плюс часы, по которым зафиксировано постоянство скорости копья, есть пример инерциальной системы отсчета. В ней движение по инерции равномерно и прямолинейно. Значит, исполняется первый закон Ньютона. Все остальные системы отсчета физики называют неинерциальными. Опыт Леона ФукоЗа неинерциальной системой отсчета совсем не обязательно отправляться в космос. Не требуется никаких межзвездных кастрюль и «летающих тарелок». Можно остаться на Земле, пойти в городской сад и покататься на «колесе смеха» — горизонтальном скользком вращающемся диске. Вы на себе почувствуете неинерциальность системы отсчета, связанной с диском, — очень быстро окажетесь отброшенным прочь от центра вращения. Можно поехать в Ленинград и посетить Исаакиевский собор. Там ясно видно, что и система отсчета, связанная с Землей, тоже неинерциальна. Дорого бы дал Галилей за идею опыта, поставленного в 1851 году французским физиком Леоном Фуко. На протяжении нескольких минут этот опыт просто и наглядно доказывал то, что великий итальянец стремился доказать всю жизнь — вращение земного шара. Теперь знаменитый эксперимент Фуко постоянно демонстрируется в Исаакиевском соборе. На длинном (98 метров) подвесе раскачивается массивный шар. В каждом качании он летит из края в край обширного помещения над полом, расчерченным четкими прямыми линиями. Маятник Фуко — вроде копья, которое мы с вами швыряли в космосе. Разгоняется он, правда, земным тяготением, но благодаря инерции сохраняет плоскость своих колебаний. Земля же, медленно поворачиваясь, сдвигает из-под нее пол собора. Летящий шар чуть-чуть сворачивает от прямых линий, начерченных на полу. Через две-три минуты накапливается весьма заметное отклонение. Простейший вывод: Земля вертится. Более тонкий вывод: система отсчета, связанная с земным шаром, неинерциальна. Но справедливы ли в этом случае уравнения механики? Можно ли применить формулу второго закона? Действуют ли на маятник Фуко (или лучше все-таки на наше «космическое копье» — дабы не мешало притяжение Земли) какие-то силы? Да. Пусть второй закон торжествует: раз есть ускорения, значит, есть и силы. Эти силы, под влиянием которых наше копье «само» ускоряется, тормозится, сворачивает вбок в неинерциальной системе отсчета, принято называть силами инерции. С такой точки зрения на колесе смеха вы оказались во власти центробежной силы инерции. Она-то и согнала вас с диска. А маятник Фуко был подвержен силе инерции Кориолиса (по имени физика, который ее впервые изучил). Она действует на тела, движущиеся во вращающейся системе отсчета. Благодаря ей маятник Фуко и смещает в такой системе плоскость своих качаний. Конечно, вы можете покинуть вращающуюся Землю и рассматривать качания маятника Фуко в какой-то не- вращающейся, инерциальной системе отсчета (для малых промежутков времени в качестве ее опоры годится хотя бы Луна). Тогда вы вправе заявить, что смещения пола собора вызваны никакими не силами, а именно вращением земного шара. Однако этот бесспорный факт не делает силы инерции фиктивными, что иногда неосторожно говорят. Коль уж явление разыгрывается в неинерциальной системе отсчета, силы инерции присутствуют обязательно и бывают порой очень эффективны — скажем, рвут на части быстро вращающийся маховик. Видите: «пассивное непослушание», каким выглядело свойство инерции в инерциальной системе отсчета, для неинерциальной обернулось активным действием. И еще. Обратите, пожалуйста, внимание на существенную деталь: силы инерции в равной мере ускоряют тела разной массы. Когда над дном нашей вращающейся и ускоряющейся «космической кастрюли» летят рядом свободно брошенные ядро и пуля, пути их и скорости меняются относительно кастрюли совершенно одинаково. При взгляде извне это ничуть не удивительно. Ведь кастрюля-то одна, она вращается или ускоряется одинаково и для ядра, и для пули. Все же подмеченный сейчас факт очень многозначителен. В нем раскрывается некое (пока чисто формальное) сходство между инерцией и тяготением (тяжесть столь же «равнодушна» к массам тел, когда сообщает им ускорение). Придет время, об этом сходстве мы поговорим побольше и поподробнее. Действие без противодействияИ, наконец, самое, на мой взгляд, странное качество сил инерции. Это единственный вид сил, не подчиняющийся, оказывается, третьему закону Ньютона. Когда брошенное копье сворачивает в сторону от прямой, проведенной по дну вращающейся «кастрюли», оно не воспринимает никакого противодействия, потому что ни с чем как будто не связано. Тут стоит вспомнить, что в прошлом веке австрийский физик Эрнст Мах сделал на этот счет одно очень заманчивое предположение. Вот что он допустил (без всякого доказательства): через свойство инерции любое тело соединено какими-то невидимыми «нитями» или «пружинами» со всей, пусть даже безмерно удаленной, материей Вселенной. Бесчисленные звезды — это, как говорил Мах, «не бумажные фонарики». Разбросанные тут и там в безграничном мире, они каким-то способом сообща действуют на каждую звезду или планету, на каждый камень, копье, пушинку — и заставляют их хранить покой или равномерное прямолинейное движение относительно инерциальных систем отсчета. Или, если хотите, сообщают им ускорения в неинерциальных системах, порождая силы инерции. Окажись этот «принцип Маха» справедлив, силы инерции стали бы подчинены третьему закону механики. Как и все прочие силы. Действие звезд на копье — вот что сдвигало бы его с прямого пути в неинерциальной системе отсчета. И вся материя мира поворачивала бы плоскость качаний маятника Фуко над полом Исаакиевского собора. Наоборот, копье, «привязанное» принципом Маха к звездам, оказывало бы при ускорениях противодействие на звезды. Выходит, бросая мяч, вы толкали бы в обратную сторону всю Вселенную? Вроде того. Это, пожалуй, приятно — быть в силах толкнуть весь мир! Но я снова вынужден предостеречь своих читателей от поспешности. Верен или неверен принцип Маха, можно будет судить только в самом конце этой книжки. Все-таки я не стерплю и уже сейчас скажу вам: увы, в современной науке принципу Маха места пока не нашлось. Надеюсь, это признание не охладит читательский интерес. Я ведь старался, чтобы сильнее всего вы удивились не инерции, а тяжести. Чуду падающих ядер и пуль, пушинок и сосулек. Именно от этого удивления нам предстоит попытаться убежать. Таким образом, об основаниях классической механики сказано уже довольно много. Разобрано поведение падающих тел, объяснены все три закона, отмечены некоторые тонкости. Пора кое-что сказать о конкретных делах ньютоновской механики, о ее замечательных достижениях в объяснении природы. Глава 4. МОГУЩЕСТВО МЕХАНИКИ Дорога в школуЯ думаю, древнегреческие школьники были ничуть не глупее современных пионеров, даже из числа отличников. И учителя у них были, быть может, неплохие. Вся разница в уровне знаний. Учителя помнили слова своих учителей, которые еще очень мало знали, еще не умели смотреть в глубь вещей. Видя быстро летящее копье, заброшенное сильной рукой, хотелось сказать, что сила рождает скорость. Так и говорили, и учили, и заучивали. А это была ошибка, ибо сила дает не скорость, а ускорение. Видя лист, падающий медленнее шишки, обобщили это на все тела и объявили, что тяжелое падает быстрее легкого, — снова ошибка. Видя восходящее и плывущее по небосводу Солнце, уверовали, что оно кружится вокруг Земли. Так и записали в священных книгах, а потом, спустя века и тысячелетия, гнали в тюрьмы и на костер несогласных и прозорливых. Ошибки громоздились друг на друга, сбивали с толку, путали мысли, вживались в сознание. Из этих ошибок, освященных религией, авторитетами, традициями, строилось представление о мире — очень наивное, неверное, непохожее на наше. С такой «моделью мира» было трудно искать истину даже людям умным и талантливым. И все-таки от года к году, от века к веку копились крупицы истины. И вспыхивали открытия. Рождались, учились, поднимали головы гениальные первооткрыватели. Их мудрость — мудрость Коперника, Галилея — вырастала в стройную систему науки. Пробил час — и прозвучал голос Ньютона, подарившего человеку новое зрение — физику, охватившую весь необозримый мир. Знание, в отличие от искусства, не бросается в глаза. Оно всегда неприметно, скрыто в скромных словах или сухих строках формул. Вероятно, поэтому на уроках физики мы редко удивляемся откровениям ньютоновских законов. И напрасно. В учении Ньютона все, с начала до конца, достойно удивленного восхищения. Земля и яблокоКлассической механике подвластны разнообразнейшие силы. Тянут железо магниты, отталкиваются от дороги колеса автомобиля, ударяются, расходясь в стороны, бильярдные шары — все это неукоснительно подчиняется законам Ньютона. Но раз уж мы в этой книжке размышляем о падающих телах, побеседуем поподробнее об одной только силе тяготения. Я уже много говорил о ней, вездесущей и таинственной, вместе с вами доискался ее главной особенности — неизменной пропорциональности тяжелой массе тела, недоумевал по поводу ее странного «действия без прикосновения». Эта поразительная ее особенность остается для нас загадкой, которую на этих страницах еще рано пытаться разгадывать. Но хоть мы не в состоянии объяснить, почему сила тяжести проникает через пустоту, нам пора задуматься над тем, как это происходит. Сегодня всем известно: вдали от Земли тяжести нет. Это ясно каждому шестикласснику, это вошло в сознание из бесчисленных книжек, газетных статей, радиопередач. Во времена же Ньютона мир выглядел иным. О том, что сила тяжести не везде одинакова, лучшие умы могли только догадываться. Никаких опытов, свидетельствующих о ее уменьшении с высотой, не было. Наоборот, на башне и в подвале тяжелое ядро представлялось одинаково тяжелым. И все-таки Ньютон, приглядевшись к перемещениям небесных тел, уверенно заявил: с увеличением расстояния от Земли тяготение убывает.
А как убывает? Быть может, на высоте облаков уже нет тяготения? Если верить упорной легенде, Ньютон ответил на это «как», созерцая в своем саду падающее яблоко. На самом деле, если и существовало это историческое яблоко, то, разумеется, не оно одно навело великого физика на его открытие. Были и другие, куда более существенные подсказки: замечательные идеи и вычисления Галилея, прозорливые слова Кеплера и математические закономерности, подмеченные им в движении планет, нескончаемые размышления самого Ньютона об инерции, массе, падении тел. Догадка эта даже сегодня не может представиться легкой и естественной. Если она и проста, то наверняка гениальна. Сила тяготения F пропорциональна массам притягивающихся тел m1 и m2, но она убывает тем сильнее, чем больше становится квадрат расстояния между центрами притягивающихся масс r2. Именно квадрат! Не просто расстояние, не куб его, а квадрат. И именно между центрами масс. Дело происходит так, как если бы вся масса каждого тела была сосредоточена в бесконечно малом объеме — в точке, совпадающей с центром тяжести. Понять и обосновать это Ньютону стоило больших трудов. Такова сущность замечательного ньютоновского открытия, которое вскоре стало знаменитым и получило название закона всемирного тяготения. Вот формула:  Символ ? означает «постоянную тяготения» — множитель пропорциональности, уравновешивающий обе части равенства. Физический его смысл прост — это сила притяжения двух тел массой по грамму, находящихся в сантиметре друг от друга. ? можно узнать из эксперимента: измерить эту силу, заставив притягиваться два шарика с массой по грамму, подвешенных рядом на тонких нитях в сантиметре друг от друга. В таком грубом опыте, правда, никакого измерения не получится — граммовые шарики притягиваются ничтожно слабо. Успех здесь принесен другим, более тонким опытом, выполненным английским физиком Кавендишем. Всемирный закон на столе
Кавендиш тонко задумал и исполнил свой эксперимент. В тщательно откачанном стеклянном баллончике висит на тоненькой нити легкое коромысло со свинцовыми шариками на концах. Перед ними укреплены большие свинцовые шары. Таким образом, коромысло с маленькими шариками обладает незначительной массой (стало быть, и инерцией), а сила притяжения крупных шаров достаточно велика. В результате совместные усилия двух шаров чуть-чуть сдвигают коромысло. Маленькие шарики с еле заметным ускорением «падают» на большие. Нить слегка закручивается. Но на ней подвешено легонькое зеркальце, отражающее световой луч. Где-то далеко, на стене лаборатории, укреплен экран с делениями, по которому скользит световой зайчик от луча, отраженного зеркальцем. И поэтому почти неуловимое закручивание нити заставляет световой зайчик перемещаться по экрану. Так закон всемирного тяготения был впервые проверен в лаборатории. По смещению светового зайчика Кавендиш рассчитывал силу притяжения шариков. Меняя их массы, ученый доказал справедливость того, что записано в числителе формулы закона тяготения: пропорциональность силы обеим тяготеющим массам. А варьируя расстояние между шарами, он подтвердил обратную пропорциональность силы притяжения именно квадрату расстояния. Но главное, что он узнал, — это значение постоянной ?. Ведь и массы, и силы, и расстояния были измерены — осталось вычислить постоянную тяготения. Она оказалась равной 6,7·10-8см3/(г·сек2) Дальше следует феерический фонтан волшебства ньютоновской механики. Взвешиваем планетуЧто бы такое взвесить поудивительнее? Хотите Землю? Пожалуйста! К вашим услугам формула всемирного тяготения. Вместо Земли можете положить на весы яблоко. Получилось сто граммов. Это масса яблока mя. На весах и гирях всегда проставлены именно единицы массы. Чтобы получить силу тяготения F, вспоминаем второй закон Ньютона и массу яблока множим на земное ускорение g, то есть 100 г·981 см/сек2. Это вес. Рискуя показаться навязчивым, я напомню, что когда-то мы определяли его как давление тела на опору, потом — как силу тяготения, исходящую от центра масс Земли и приложенную к телу. Разумеется, яблоко, притягиваемое Землей, давит на опору. В свою очередь, опора давит на яблоко — исполняется третий закон. А потому между яблоком и опорой мы вправе поместить пружину. Она сожмется тем сильнее, чем сильнее тяготение. Вот мы и измерили с помощью весов земное притяжение. Знаете радиус Земли? Напомню — 6300 километров, или 6,3·108 см (перед вычислением все величины нужно свести к одной системе единиц). Теперь можно вычислить. Масса Земли mз=Fr2/(?·mя) = 100г · 981 см/сек2 · (6,3·108 см)2 /(6,7·10-8 см3/(г·сек2) ·100 г) = 6·1027 г = 6·1021 т. Подсчитали? Загляните в энциклопедию — масса Земли именно такова. Вот и свершилось волшебство — по весу яблока определена гигантская масса планеты. Это вас не восхищает? Без весовПожалуй, будет лучше, если внимательный читатель вместо восхищения поймает автора за рукав и сделает ему замечание: по формуле закона всемирного тяготения массу Земли можно было определить и без взвешивания яблока. Ведь если вес яблока F = mяg, а r — земной радиус, то масса Земли mз = mяgr2/(?mя) = gr2/? Масса яблока в числителе и знаменателе сокращается. Формула открывает удивительную возможность взвешивать Землю вообще без всяких весов — по постоянной тяготения и величине ускорения силы тяжести. Если вы забыли значение g, покараульте с секундомером в руках возле какой-нибудь яблони, засеките время, за которое очередное яблоко пролетело с ветки до земной поверхности, потом измерьте высоту ветки, по галилеевской формуле s=gt2/2 (из первой главы этой книжки), подсчитайте g и вставьте в только что выведенную формулу mз= gr2/?. Через минуту вычислений вы узнаете, во всей ее огромности, земную массу. Узнаете количество вещества своей планеты! Недаром Кавендиш, который, разумеется, превосходно помнил значение g, назвал свой исторический эксперимент, позволивший впервые вычислить постоянную тяготения «взвешиванием Земли». Он узнал ? и сразу подсчитал, какова масса земного шара. Этим уже стоит чистосердечно восхититься. Да, падающее яблоко многое могло подсказать наблюдательному Ньютону. На вышинеДогадываетесь, в чем секрет замечательного умения, которым вы овладели вслед за Ньютоном и Кавендишем? Секрет в том, что использовано равенство тяжелой и инертной масс: ведь в числителе формулы стояла инертная масса из второго закона Ньютона, а в знаменателе — тяжелая масса из закона всемирного тяготения. Мы их сократили и были вправе сделать это только потому, что они не в состоянии «переспорить» друг друга, или, иначе говоря, только потому, что все тела падают одинаково быстро. Так из явлений маленьких, ежеминутно происходящих на наших глазах, вырастают закономерности широчайшего охвата. Не в отвлеченном рассуждении, не в расплывчатой фразе, а в конкретном деловом расчете физик совмещает песчинку с планетой. Предсказания Ньютона широки и многообразны. Вы хотите узнать, сколько будет весить килограммовая буханка хлеба на вершине Монблана? Пожалуйста, используйте формулу всемирного тяготения. Получится 997 граммов. Пожелали выяснить значение ускорения силы тяжести на высоте орбитального полета Гагарина — та же формула даст вам ответ. Проделайте вычисления, и вы убедитесь, что оно там уменьшится незначительно — всего на одну шестнадцатую часть. На столько же уменьшился бы и вес. Это неожиданно для наивных людей, полагавших, что спутники невесомы из-за удаления от земного шара. Боюсь, самым любопытным из читателей уже захотелось взвесить Солнце. А почему бы и не взвесить? Взвешиваем СолнцеЭто весьма просто. Расстояние до Солнца спросим у астрономов. Они скажут: 150 000 000 километров. Кроме того, мы знаем, что Земля падает на Солнце, хоть и не может упасть. Об этом странном факте нелишне поговорить поподробнее, пользуясь законами Ньютона. Благодаря своей инерции Земля постоянно стремится улететь от Солнца по прямой (первый закон Ньютона). Вместе с тем Земля испытывает солнечное притяжение (закон всемирного тяготения) и приобретает ускорение, направленное к Солнцу (второй закон Ньютона). Эти два движения складываются — получается вечное обращение Земли вокруг Солнца. Стоит напомнить, что свободное падение отнюдь не обязано быть отвесным. Пуля, вылетевшая из дула пистолета параллельно земной поверхности, приближается к ней так же быстро, как и пуговица, упавшая со стола. Земля как пуля. Она не отвесно падает на Солнце. Каково же ускорение падающей Земли? Длину земной орбиты подсчитать проще простого. Эта орбита — круг радиусом 150 миллионов километров. Помножьте радиус на «два пи» (6,28) — выйдет миллиард километров. Время — 365 суток, год нашей жизни. Отсюда нетрудно подсчитать, что за секунду Земля успевает пролететь 30 километров по своей орбите и одновременно упасть к Солнцу на три миллиметра. По формуле Галилея S =act2/2 сразу же получаем значение ускорения Земли к Солнцу: ас = 0,6 см/сек2. Маловато, конечно. Но зато мы можем не опасаться катастрофического столкновения со своим жарким светилом. Масса Солнца теперь выясняется автоматически: 2·1027тонн. Обратите внимание, на этот раз нам не понадобилась масса Земли. Достаточно было знать ускорение ее падения на Солнце. Любое тело, находящееся на земной орбите, будет падать к Солнцу с тем же ускорением — 0,6 см/сек2. Так в астрономическом масштабе продолжает действовать постоянство ускорения свободного падения для тел каких угодно масс. Явление, которое мы подметили на сосульках, падающих с карниза! Ангелы-бездельникиОт Солнца переходим к планетам. Было время, когда неглупые люди всерьез полагали, что планеты все время подталкиваются ангелами, потому-де они и движутся. На каждую по ангелу. Как следует из ньютоновских законов, ангелы эти — бездельники. Планеты великолепно обходятся без них: по инерции летят прямо, а влекомые солнечным тяготением, падают на светило. В результате сложения этих двух движений планеты сворачивают с прямого пути и движутся по эллипсам — так называют в геометрии фигуры, похожие на овал. Сумма расстояний точек эллипса от двух точек, лежащих внутри фигуры и называемых фокусами, постоянна (это геометрическое определение). В одном из фокусов всегда находится Солнце. Это знал еще Кеплер. Если же фокусы совпадают, получается круг. Многие планеты (в их числе наша Земля) движутся по почти точным кругам. Ньютон разработал тонкий математический метод для вычисления планетных путей и решил с его помощью массу трудных задач. Удалось найти зависимость периодов обращения двух разных планет (длительность «годов») от близости планет к Солнцу. Кубы наибольших расстояний планет, на которых они оказываются в своем движении вокруг Солнца, пропорциональны квадратам их «лет». И эта особенность, гениально угаданная Кеплером, нашла подтверждение в строго обоснованной теории Ньютона, который, однако, внес уточнение — зависимость от масс планет. В разных местах эллипса движение неодинаковое: с приближением к Солнцу оно ускоряется, с удалением от Солнца — замедляется. Как меняется скорость, подметил тот же Кеплер (радиус, проведенный от планеты к Солнцу, в равные промежутки времени «выметает» одинаковые площади). А Ньютон дал доказательство. В конце концов удалось составить подробнейшее «небесное расписание» движения планет. И — ни одного ангела! Или, как заметил один физик, должность ангела занимает само Солнце. Всеобщее послушаниеРасписание исполнялось с отменной точностью. Планеты следовали по орбитам с предсказанной скоростью, их уверенно находили в предсказанных местах неба. В назначенные часы, минуты и секунды происходили восходы, заходы, противостояния, затмения Солнца и Луны. Солнечная система голосовала за механику Ньютона, за всемирное тяготение. Единственное исключение — одна малая особенность в движении Меркурия, не уложившаяся в предсказания ньютоновской небесной механики. Об этом пойдет речь далеко впереди. А как обстояло дело за пределами Солнечной системы? Послушны ли Ньютону звезды? Да, послушны. Этот ответ был получен наукой уже после смерти великого физика, когда развилась звездная астрономия. Особенно красноречивы многолетние наблюдения так называемых двойных звезд, тех, что находятся по соседству и медленно кружатся одна вокруг другой. Есть убедительный документ, свидетельствующий о том, что этот звездный вальс точно следует ньютоновскому закону — фотографии взаимного расположения звездной пары Сириус А — Сириус В, сделанные на протяжении одного почти полного оборота этой пары — с 1862 до 1904 года. Чертеж орбиты Сириуса В — это типичный эллипс. И звезда путешествует по нему именно так, как назначено ньютоновской небесной механикой: чем дальше от Сириуса А, тем медленнее движется Сириус В. Возле фокуса он за шесть лет успевает пробежать такое же расстояние, какое вдали от фокуса преодолевает за шестнадцать. Это как раз и требует теория тяготения! Шагнем дальше в ширь Вселенной. Слушаются ли Ньютона целые звездные города? В нашей Галактике ученые отыскали изумительно красивые звездные рои — шаровые скопления. Чем ближе к центру скопления, тем больше звезд. Но даже в глубоких недрах его, где на фотографии получается сплошной белый фон, звезды настолько далеки друг от друга, что сталкиваться не могут. Они всегда действуют друг на друга только тяготением. Поэтому скопления и круглы — центральные области притягивают периферийные. Та же причина сделала шарами нашу Землю, Солнце и все планеты. Даже в галактиках — необозримых скопищах звезд и звездных систем — астрономы находят явные следы мощного тяготения. Оно действует даже в фантастически гигантских скоплениях галактик, пронизывает всю Вселенную. На кончике гусиного пера
Самый яркий эпизод торжества идей Ньютона относится к первой половине прошлого века. Тогдашние астрономы никак не могли втиснуть в рамки ньютоновской теории движение Урана, недавно открытой и самой дальней из известных в ту пору планет. Уран двигался, в общем, так, как требовало «расписание», но в тонкостях нашлись непонятные отклонения. Планета немножко выходила из назначенного курса, слегка искривляла эллипс своей орбиты. Чтобы объяснить эти особенности, астрономы учли в расчетах не только солнечное притяжение, но и тяготение соседних с Ураном планет-гигантов Юпитера и Сатурна. Тем не менее все странности поведения Урана не удалось объяснить. Значит, Ньютон не прав? Его механика в чем-то грешит? Положение сложилось драматическое. И вот двое ученых — англичанин Адаме и француз Леверье — независимо друг от друга сделали предположение, которое витало в воздухе и напрашивалось само собой: а нет ли за Ураном еще одной планеты — очень далекой, слабо светящейся и потому еще не замеченной? Опять заскрипели перья, выписывающие уравнения небесной механики. Теперь их спрашивали: где искать неведомую планету, вызвавшую возмущения в движении Урана? Уравнения дали свой математический ответ: в такие-то моменты времени загадочная планета должна находиться в таких-то местах неба. Леверье и Адаме послали расчеты в несколько обсерваторий. И когда астрономы-наблюдатели направили телескопы так, как посоветовали их корреспонденты- теоретики, планета действительно нашлась. Маленькая, едва заметная. Ей дали имя Нептун. И отпраздновали знаменательную победу теории тяготения. Это было в 1846 году. Спустя 84 года при таких же примерно обстоятельствах американцу Томбо удалось открыть самую далекую из наших планет — Плутон. На кончике авторучкиСовсем недавно, в 1964 году, произошло еще одно удивительное событие. Уравнения небесной механики помогли американскому астроному Ван де Кампу понять причину ничтожных колебаний Летящей звезды Барнарда — одной из ближайших к нам звезд, названной так за свое быстрое движение. Казалось бы, раз где-то в космосе летит звезда, так уж пусть она летит по инерции прямо — как велено первым законом Ньютона. А она «болтается». Правда, чуть-чуть — за год на десять угловых секунд, самое большее. Но и этого достаточно, чтобы взяться за вычисления. Подробная расшифровка колебаний привела к замечательному и долгожданному успеху: впервые с полной достоверностью было доказано существование планеты, вращающейся вокруг далекой звезды. Эта планета, действуя своим тяготением на звезду, заставляет ее мчаться не по прямому, а по слегка волнистому пути. Ван де Камп выведал немало подробностей о невидимом спутнике звезды Барнарда. Он весьма массивен — в полтора раза тяжелее нашего Юпитера (а Юпитер в 318 раз тяжелее Земли). Путь спутника — довольно вытянутый эллипс. Самое большое расстояние его от звезды Барнарда — 660 миллионов километров. Год — в 24 раза дольше нашего. Анкета, как видите, получилась довольно полная. И все это сказано про небесное тело, которое никто никогда не видел и, быть может, не увидит. Такова проницательность науки. Той самой науки, которая началась с опытов Галилея, бросавшего ядра и пули с Пизанской башни. Ведь спутник звезды Барнарда тоже «падает», и по тем же законам! Впрочем, тут особенно ясно, что и звезда падает — это ее падение ведь и выдало таинственного спутника, показало, что она не одинока. Так и должно быть: звезда тянет спутник, который, в свою очередь, тянет звезду. Действие равно противодействию. Не видя ЛуныЕсть анекдот. На экзамене профессор спрашивает студента: Вы видели Луну? Нет! — поспешно отвечает студент, мечтающий избавить себя от новых вопросов. Но даже если бы хитрый студент и в самом деле ни разу в жизни не поднял глаз на Луну, все равно он мог бы немало узнать о ней. По той же самой причине, по которой Ван де Камп открыл и описал невидимый спутник звезды Барнарда. Важно то, что падает не только Луна, но и Земля. Обе они, влекомые тяготением, стремятся к общему центру масс. Какие же события вызываются на Земле ее падением на Луну? Очень заметные и существенные. Прежде всего приливы и отливы. На вопрос: «Почему бывают приливы и отливы?» — часто отвечают: «Очень просто, воду океана притягивает Луна». Считают так: под Луной на океанской поверхности вырастает огромный водяной горб, а так как Земля под Луной вращается, то горб этот перемещается, дабы все время оставаться «подлунным», и набегает в конце концов на берег. Согласны? Ответ неверен. Если бы дело происходило так, то приливы и отливы наступали бы всего один раз в сутки. А они бывают дважды в сутки. На самом деле водяных горбов на поверхности Мирового океана два — первый действительно под Луной, а второй в диаметрально противоположной стороне. И вершина второго направлена от Луны. Оба горба сохраняют свое положение в пространстве, а Земля кружится, вот и выходит, что приливная волна дважды в сутки заливает берега. Но почему же все-таки горбов два, а не один? И почему второй словно бы отталкивается от Луны? Никакого отталкивания нет. Причина этого явления в том-то и состоит, что Земля вместе с Мировым океаном непрерывно падает в сторону Луны, хоть и не может «упасть», так же как и Луна не может упасть на Землю. Прямо под Луной лунное притяжение сильнее (потому что там океан ближе к Луне) и, значит, больше ускорение падения. «Подлунный» горб падает быстро. А с обратной стороны Земли океан на двенадцать тысяч километров дальше от Луны, там ее тяготение слабее, и вода отстает в падении. Здесь я задам вам проверочный вопрос (из числа довольно трудных — на нем иногда проваливаются даже студенты-физики). Кроме лунных, по океану бежит еще пара приливных горбов, рожденных притяжением Солнца. Они гораздо меньше, чем лунные. Почему? Вертится на языке фраза: потому, что Солнце притягивает воду океанов слабее, чем Луна. Так и говорят иные незадачливые студенты на экзаменах, огорчая терпеливых экзаменаторов, ибо ответ этот грубо ошибочен. Солнце влечет к себе Землю (и все, что на ней есть, в том числе и океаны) неизмеримо сильнее, чем Луна. Ведь не вокруг Луны, а именно вокруг Солнца обращается наша планета. А невелики солнечные приливные волны на Земле потому, что наше светило очень уж далеко — в 150 миллионах километров. В пять с лишним тысяч раз дальше, чем Луна. Это значит, что земной диаметр по сравнению с расстоянием до Солнца ничтожно мал. Следовательно, весьма незначительна и разница в силе солнечного тяготения по ту и другую сторону нашей планеты. Другими словами, на дневной и ночной сторонах Земли вода океана падает к Солнцу с очень близкими ускорениями. Поэтому и невелики солнечные горбы. Все дело, как видите, в том, что по сравнению с расстоянием Земля — Луна наша планета довольно велика, а по сравнению с расстоянием Земля — Солнце мала. Для солнечного тяготения Земля — точка, для лунного — отнюдь не точка. Вот и ответ на хитрый экзаменационный вопрос.
Вообще, подробная картина приливов получается довольно сложной и запутанной. Но для понимания ее не требуется ничего, кроме знания ньютоновской механики, теории тяготения и, конечно, карты береговой линии материков. Есть, кстати сказать, и приливы суши, потому что земная кора не абсолютно тверда. Глава 5. ЗОРКИЙ МАЯТНИК Открытие в собореФормулы Ньютона отлично действуют «на земле, в небесах и на море». Этого мало. Они сохраняют свою власть и под землей. Зная теорию тяготения, человек смотрит через планету, в глубь земных недр. И «глаз» для такого необыкновенного зрения самый простой из всех физических приборов — маятник. Давно пора нам поподробнее поговорить о маятнике. Он сыграл и продолжает играть почетную роль в науке. Помните, в третьей главе шла речь о маятнике Фуко? Благодаря инерции он сохранял плоскость качаний и доказал тем самым вращение Земли. А вот другая примечательная особенность маятника. Ее первым подметил все тот же неутомимый Галилей. Тогда он был еще студентом. Посещал, как положено, богослужения в Пизанском соборе. И во время скучных месс развлекался разглядыванием массивных бронзовых люстр- Они были красивы, эти люстры, ибо сработаны самим Бенвенуто Челлини. Но особенно любопытно было наблюдать их мерные покачивания после того, как служитель, зажигавший свечи, ненароком толкал их своим длинным шестом. Во время богослужений, молитвенно обратив лицо к своду собора, можно было без помех наблюдать за качаниями люстр. И Галилео подметил: люстра качается, строго соблюдая ритм. Размахи происходят в одинаковое время. Правда, у Галилео, по обыкновению, не было часов, да и неловко было бы в соборе то и дело смотреть на них. Все-таки он умудрился измерять время — по ударам своего пульса. Так Галилей сумел поставить физический опыт в церкви. Нашел и объект эксперимента, и измерительный прибор — собственное сердце. Еще характерный штрих: открыв странную особенность маятника, он сразу же применил ее на пользу делу — устроил регистратор пульса, хороший инструмент для врачей. Это были, по существу, первые маятниковые часы, которых теперь так много на нашей планете. Свойство, открытое Галилео, называют изохронностью. Период колебаний (время каждого полного размаха Т) зависит у математического маятника (тяжелого тела, качающегося на легкой нити) только от длины нити, точнее — от квадратного корня длины. Масса же груза может быть любой. Эту закономерность знал уже Галилей. А полную формулу вывел голландский ученый Ганс Христиан Гюйгенс, последователь Галилея и современник Ньютона. Вот эта формула: 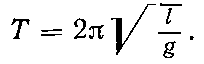 Вы спросите: а при чем тут теория тяготения и подземное царство? Чуть-чуть терпения. Соревнуемся с ГалилеемВ формуле маятника под знаком квадратного корня в знаменателе красуется g — то самое ускорение свободного падения, о котором мы не раз говорили в этой книжке. Это и понятно. Ведь маятник, когда качается, падает. Правда, не свободно, но падает. А никакое падение не обходится без g. И здесь оно поэтому налицо. Причем из качаний маятника его очень просто определить, и, что весьма приятно, без всякой спешки. Не надо бросать тел с Пизанской башни или катать отшлифованные шары по желобу. Достаточно сделать маятник (подвесьте тяжелую гайку на длинной нити), тщательно измерить расстояние от точки подвеса до центра тяжести, чуть-чуть подтолкнуть его и сосчитать, сколько колебаний он совершит, скажем, за час. Хорошо бы не прибегать во время опыта к современным секундомерам или хронометрам. Время лучше отмерить по самодельным солнечным часам (как их устроить, рассказано в школьном учебнике астрономии) . Если вы не поленитесь и исполните такой опыт, то перещеголяете самого Галилео Галилея. При помощи пустяковых подручных средств, которыми, конечно, располагал знаменитый основоположник экспериментальной физики, сумеете сделать то, что так и не смог сделать этот гениальный итальянец, несмотря на все свои старания: измерить значение g. Если будете аккуратны, то получите по крайней мере две первые цифры этой знаменитой физической величины (даже если используете для отсчета времени солнечные часы). А Галилей, катая по желобу свои шары, ошибся, измеряя g, в два раза! Впрочем, не очень радуйтесь. Галилей ведь не знал, что g стоит под корнем в знаменателе правой части формулы маятника, а вы эту формулу получили прямо из рук Гюйгенса. Будет совсем хорошо, если вам захочется узнать, как она выводится, — для этого требуется немного, всего лишь заглянуть в учебник физики. Сделайте это. И очень советую вам поставить опыт. Лучше с пониманием дела повозиться над маятником и солнечными часами, чем без всякого понимания спаять по готовой схеме транзисторный радиоприемник. А теперь легко понять, как маятником заглядывают в земные недра. Причем заглядывают, не глядя в них! Как Джо нашел кладВ давние времена кровожадные пираты на некоем необитаемом острове зарыли в землю клад — сто тысяч свинцовых сундуков, набитых награбленным золотом. Как водится, пираты потеряли карту с указанием места клада и от огорчения перерезали друг другу глотки. Знакомый сюжет? Много таких вам, наверное, попадалось, начиная с «Острова сокровищ». Я предлагаю новую идиллическую и научно-просветительную концовку. Через пятьсот лет поселились на острове престарелый Джо (бравый моряк в отставке) и толстушка Кетти (его верная супруга). Джо построил уютный домик, промышлял рыбной ловлей, Кетти готовила пудинги и т. д. Все было бы хорошо, если бы не постоянные размолвки добрых супругов по поводу времени. У Джо был превосходный морской хронометр, у Кетти — не менее надежные кухонные ходики с маятником и кукушкой. И вот каждый день происходили диалоги: — Эх, Джо! Твой хронометр опять отстал. Боюсь, пружина ослабла. Это твои ходики бегут невесть куда. За сутки на целую минуту! В конце концов разногласия надоели. Джо отвез хронометр и ходики на материк. Отдал знакомому идеально честному часовщику, который почистил и смазал часы, а исправлять не стал: они оказались точными. Но на острове вновь начался разнобой. Опять ходики опережали хронометр. И Джо решил самостоятельно доискаться причины. Он сел за книги, обложился сочинениями Гюйгенса, Ньютона и, начитавшись, стал размышлять. «У хронометра, — думал он, — баланс с пружинкой и период его колебаний не зависит от силы тяжести. А у ходиков — маятник, качания которого зависят от поля тяготения в данном пункте земной поверхности...» Дойдя до этого места своих размышлений, Джо весело воскликнул: Ого! Дай-ка, женушка, лопату! А получив лопату, полез в подвал под кухней, разобрал пол, несколько раз копнул землю — и наткнулся на огромный клад, тот самый штабель сундуков с золотом, что был зарыт пятьсот лет назад неизвестными пиратами. Судьба распорядилась так, чтобы дом счастливого семейства оказался как раз над кладом! По-моему, конец неплохой. Тем более, что Джо и Кетти взяли себе совсем маленькую толику золота, а остальное пожертвовали в фонд развития науки. Взгляд в недраВ чем тут дело — ясно. Золото плотное, масса его большая. Оно добавило свое маленькое притяжение к общей силе земного тяготения. И когда маятник ходиков оказался над кладом, то стал раскачиваться чуть- чуть чаще, чем в других местах. Ведь усиление поля тяжести увеличило ускорение падения, g над кладом стало чуть больше, и период качаний уменьшился. Усидчивый Джо это и сообразил. Он мог бы, если бы захотел, не разрывая клада, узнать, сколько зарыто золота, — маятник помог бы подсчитать вызванную кладом добавку к силе тяжести и, стало быть, узнать его массу. Самые дотошные читатели могут, сделав некоторые допущения, выполнить соответствующий подсчет. В предыдущем разделе сообщены все условия задачи. Получится, конечно, что клад фантастически огромен. Пиратские клады этим способом не ищут — они все- таки маленькие. Зато клады полезных ископаемых — сколько угодно.
Маятник отлично «видит», например, подземные озера нефти. Нефть имеет невысокую плотность, масса ее скопления сравнительно небольшая, поэтому маятник качается над ней чуть реже, чем над плотными породами — гранитом или базальтом. Профиль планетыИ еще маятником удобно ощупывать фигуру Земли. Над тем местом, где планета «толще», g больше и качания маятника чаще. Наоборот, над «тонкими» местами Земли качания пореже. Так узнали, что под полюсами Земля тоньше, чем под экватором. Значит, она приплюснута. Качая маятники над горами и долами, над болотами и пустынями, над морями и полями, ученые сумели нарисовать довольно подробно своеобразную фигуру Земли, которая, при ближайшем «рассмотрении» маятниками, оказалась вовсе не шаром. Для геометрической фигуры планеты математики придумали специальное слово (увы, без всякой лингвистической изобретательности)— геоид. Это означает просто «земной», «землеподобный». А в последние годы в помощь неутомимым маятникам поставлены «небесные землемеры» — искусственные спутники. Вы, конечно, помните, что спутник, облетая планету, непрерывно на нее падает. И там, где поле тяжести сильнее (то есть Земля либо «толще», либо имеет крупные массивы плотных пород), спутник, падая быстрее, слегка опускается. А над «тонкими» или менее плотными участками земной поверхности, наоборот, поднимается, потому что падает медленнее. Вместо гладенького плавного эллипса получается орбита со множеством местных «возмущений». Ученые ими, однако, отнюдь не возмущены, а, напротив, довольны. Смотрят астрономы в небо, фиксируют приборами траекторию космического скитальца и лучше узнают свою Землю. Потому что и земной «профиль», и внутреннее строение планеты как в зеркале отражаются в линии полета спутника. Хочется вспомнить, что в такой же, по сути дела, «возмущенной траектории» падающего тела были зашифрованы до поры неведомые науке Нептун, Плутон, спутник Летящей звезды Барнарда... И вот теория тяготения выступила в роли рентгена Земли! Что ждет АнтарктидуПод конец разговоров о маятнике — несколько слов про великолепное пророчество, которое недавно было сделано с помощью этого нехитрого прибора. Речь идет об интереснейшей и жизненно важной задаче, стоящей перед человечеством, — о грядущей судьбе ледника Антарктиды. Вопросы ставятся такие. Что происходит сейчас с этой гигантской ледяной глыбой, нависшей над Южным полюсом земного шара? Тает она или, наоборот, намерзает? И как это сказывается на уровне Мирового океана? Если масса антарктического ледника увеличивается, океан будет постепенно мелеть, уровень его — понижаться, оставляя за высохшей прибрежной полосой бесчисленные морские порты. Уменьшение же ледника вызовет, наоборот, повышение уровня океана — прибрежным городам и портам станет грозить затопление. Пусть процесс этот долог, исчисляется столетиями — все равно его надо разгадать, чтобы вовремя предотвратить угрозу. И вот в Антарктиду явились геофизики. Во многих точках ледового материка провели тончайшие гравиметрические измерения: раскачивали маятники и измеряли ускорение силы тяжести. А спустя некоторое время, обработав и обсудив полученные результаты, пришли к выводу: антарктический лед тает. Медленно- медленно уменьшается масса ледника. Значит, климат Земли едва заметно теплеет и океан мало-помалу поднимается. Это кажется колдовством: пришел в ледяную пустыню человек, покачал маятник — и предсказал будущее не только этой пустыни, этого материка, но и всей планеты! А логика рассуждений вот какая. Колдовская логикаПрежде всего геофизики выяснили, что все материки как бы «плавают» в земной коре. Увеличивается масса материка — и он погружается глубже. Уменьшается масса — он всплывает, поднимается из земных недр. Этой проблеме было посвящено обширное и очень трудное исследование. После горячих споров ученые согласились с выводом, о котором я сказал. Далее вообразим, что материки не меняют с течением времени своего веса — минуют века и тысячелетия, а их масса остается одинаковой. Тогда они не испытывают никакой «качки». Во всяком случае, вертикальных движений (погружений или всплытий) нет. И для такого нарочно упрощенного гипотетического случая удается очень точно вычислить теоретическое значение ускорения силы тяжести в любом месте поверхности любого материка. Это и было сделано. Для разных точек «неподвижно плавающей» Антарктиды путем чисто кабинетных расчетов нашли значения g. Следующий шаг — экспериментальные измерения g. Тут-то и получили слово маятники. Они сказали, каковы действительные значения ускорения силы тяжести на Антарктическом материке. Затем последовало сравнение теории с опытом. И всюду в Антарктиде действительные значения оказались чуть-чуть больше, чем теоретические. Больше! Что это могло означать? Раз больше значение g, значит, сильнее, чем «должно быть», поле тяжести. А поле тяжести увеличивается с приближением к центру масс Земли — так велит ньютоновский закон всемирного тяготения. Выходит, Антарктический материк погружен в земную кору глубже, чем если бы он был неподвижен — ведь именно для неподвижного материка были вычислены теоретические значения g. Вывод: Антарктида не неподвижна. Она движется. А как — вверх или вниз, всплывает или тонет? Всплывает. Если бы Антарктида погружалась, она стремилась бы к уровню равновесия сверху и пребывала бы выше этого уровня, то есть дальше от центра Земли. Тогда поле тяжести на поверхности материка и, соответственно, значение g оказались бы меньше, чем на уровне равновесия. Но истинное значение g вышло больше теоретического, вычисленного для уровня равновесия. Следовательно, Антарктида стремится к этому уровню снизу, находясь ниже его (ближе к центру Земли). Это и значит, что она всплывает. Ну, а всплывает то, что становится легче. Лед тает, масса его уменьшается. Так всплывает баржа, с которой разгружают арбузы. Вот она, логика колдовского пророчества, исполненного с помощью маятника! Глава 6. ЦАРИЦА МИРА Слова и понятияПора отдать должное царице мира. Так один ученый назвал энергию. Но предварительно маленькое отступление. В физике полным-полно сугубо научных терминов, в которых новичок слышит не более чем барабанный бой. Какой-нибудь «импеданц» или «лагранжиан» ничего не говорят нашим обывательским сердцам. С термином «энергия» дело обстоит иначе. Каждый лирик отлично знает, что это такое. Любой филолог со снисходительной улыбкой объяснит вам, что энергия — это работоспособность, активность, подвижность и т. д. Верно, конечно. Смысл этого слова в общечеловеческом понимании широк и емок. Однако для физика энергия — нечто иное. Нечто более тонкое и абстрактное. Вдумчивый физик (когда речь идет о физике) не станет с лету придумывать синонимы этому слову, потому что их не так-то просто подобрать. Он никогда не поставит знака равенства между энергией и подвижностью или активностью, ибо иной раз неподвижное может в физическом понимании обладать большей энергией, чем движущееся. Кроме того, тут существенно вот что. Активный человек, когда у него портится настроение, становится пассивным и вялым. Куда пропадает его «энергия»? Он ее кому-то «отдает»? Нет, его «энергия» просто проходит, исчезает. В физике же энергия не исчезает. Она неуничтожима. Если уж давать физическое определение энергии, то, пожалуй, именно это свойство надо признать основным. Так поступил, в частности, современный американский физик-теоретик и блестящий лектор Ричард Фейнман. В «Фейнмановских лекциях»[4] рассказ об энергии начинается с прямо-таки детского популяризаторского анекдота. Кубики МонтигомоШестилетний Монтигомо — Ястребиный Коготь имеет 28 игрушечных кубиков. И это число имеет свойство сохраняться, что бы ни вытворял с кубиками неутомимый хозяин. Вдруг пропадает один кубик. Но опытная мама (ее роль уподобляется Фейнманом роли физика) по выпуклости ковра находит потерянное под ковром. В другом случае поиски кубиков сложнее. Мама выполняет целое исследование. В конце концов она замечает, что в баке стиральной машины уровень мыльной воды выше обычного. Измерив превышение уровня, мама- физик вычисляет лишний объем воды, который, как выясняется, в целое число раз больше объема кубика. Вывод — в непрозрачной мыльной воде утонуло это самое число кубиков. Их-то и недоставало до полного счета. Был еще случай, когда кубиков объявилось не 28, а 30. Два лишних! Откуда они взялись, мама-физик узнает, восстановив недавнюю историю событий. Оказывается, к Монтигомо приходил в гости приятель Кожаный Чулок со своими кубиками и два позабыл. После пересказанной притчи Фейнман просит отвлечься от кубиков. Это не вещество, не предметы, не тела. Кубиков не существует. Существует же некая физическая характеристика материи и движения, сохраняющаяся при любых явлениях внутри системы, изолированной от окружающей среды. И далее излагается теорема (из области теории теплоты), которая утверждает, что в надежно изолированном процессе неуничтожимым кубикам соответствует вполне определенная физическая величина, остающаяся постоянной при любых пертурбациях. Это и есть энергия. Гвоздь в стенуК понятию энергии физика шла долго и трудно. Правда, о том, что движение не может пропасть бесследно или родиться из ничего, догадывались давно. Понимали это и Галилей, и еще более четко французский мыслитель Декарт, а за ним наш славный Ломоносов. Но то были слишком общие, чисто качественные, лишенные количественных оценок предположения. Точность, математический символ, формула родились лишь в XIX столетии. Однако в узких рамках механики сохранение энергии (без употребления этого слова) было известно и Ньютону. Причем в соответствии с сугубо механическими истолкованиями силы (как причины ускорения тел), пути (обязательно в инерциальной системе отсчета), работы (произведения силы на путь). И отправным пунктом послужили-таки мысли о механической работоспособности. Как видите, здесь употреблен тот самый термин, который, как я уже говорил, в обычном, обывательском понимании далеко не всегда отвечает физической сущности энергии. Сперва несколько простеньких выкладок. Чтобы повесить у себя над столом портрет Ньютона, я забиваю гвоздь. Бью молотком по шляпке. Гвоздь лезет в стену. На расстоянии, равном глубине (S) внедрения гвоздя, молоток прикладывает неизменную (это допускается ради простоты) силу F. Тогда при каждом ударе молоток, преодолевая сопротивление стены гвоздю, совершает работу, которая записывается так: А = F·S. Между тем, если верить второму закону Ньютона, сила измеряется произведением массы молотка на изменение его скорости во время удара. Это тоже легко записать математически. Пусть молоток, вгоняя гвоздь, затормозился от скорости v до полной остановки за время t. Тогда изменение его скорости (здесь не ускорение, а замедление, которое ради упрощения будем считать равномерным) составило: а = v/t , а сила F = mv/t Поэтому на расстоянии S = at2/2 = vt/2 была совершена работа  Эта работа выполнена за счет энергии движущегося молотка, которая, таким образом, равна этой же величине T= mv2/2 — и называется кинетической энергией. Только что добытая формула, выведенная Ньютоном, — целый рог изобилия научных откровений. По ней очень легко предсказывать, какую работу совершит движущееся тело, если его остановить. Пуля убивает волка, вода льется на лопасти турбины, брошенный камень сшибает с ветки яблоко — всюду затрачивается работа. И количество ее дается величиной Т. В этом смысле кинетическая энергия — действительно показатель механической работоспособности тела, «обещание» работы. Напоминая вам эти школьные истины, скажу еще несколько слов о другом виде энергии — потенциальной. Запас работоспособностиЯ живу в пятиэтажном доме на пятом этаже и горжусь этим. Потому что жильцы, обитающие на нижних этажах, по одному существенному признаку мне заметно уступают. Я гораздо богаче их именно потенциальной энергией. Чем выше тело над земной поверхностью, тем больше затрачено работы на его подъем. Тяжелый чемодан поднять на пятый этаж труднее, чем легкий. А на третий этаж его поднять легче, чем на пятый. Значит, работа подъема П тут зависит от веса (обозначим его теперь через р) и от высоты подъема h: П = ph. А так как вес р равен массе m, помноженной на ускорение свободного падения g, то можно написать формулу: П = mgh. Такой величиной измеряется потенциальная энергия, иначе говоря, возможность движения, запасенная в поднятом теле: ведь истраченная работа не пропадает, а остается при чемодане в виде возможности упасть, скатиться, спуститься на веревке. В поднятом теле есть неиспользованная способность к движению, к скорости — значит, и к кинетической энергии. Так же, как в расслабленной руке есть неиспользованная способность совершить удар молотком. Слово «потенциал» в переводе с латыни означает «возможность». Это, как видите, не работа. Это — запас работоспособности. Потенциальная энергия переходит в кинетическую, а та — в работу. И наоборот. Во всех движениях, где так или иначе совершается работа, происходят эти переливы. Особенно легко их заметить во всевозможных аттракционах. Качели, гигантские шаги, спиральные спуски, лыжные трамплины — неплохие наглядные пособия для начинающих знатоков механики. На русских горкахКогда речь заходит об энергии, популяризаторы да и ученые (вплоть до самого Эйнштейна) любят вспоминать аттракцион, который называется русскими горками. Тележка с седоками скатывается по рельсам с крутого склона, взлетает с разгона на другой, опять скатывается, поднимается на третий и т. д. Сперва потенциальная энергия переходит в кинетическую, потом наоборот: кинетическая в потенциальную и т. д. Причем вот существенная подробность: каждая последующая горка сделана немного ниже предыдущей. Почему? Потому что полная энергия тележки, то есть сумма ее потенциальной и кинетической энергий, в пути не может увеличиться. Это строго вытекает из законов падения тел (ведь тележка именно падает, хоть и несвободно: по извилистому пути скатывается с вершины горки вниз). В падении с нулевой начальной скоростью нельзя подняться выше точки старта. На это не хватит энергии. Конечно, при отсутствии трения и сопротивления воздуха полная энергия Е не уменьшилась бы, а сохранилась. Было бы всегда Е = Т + П = const. Вот они, механические «кубики Монтигомо»! Сохранение энергии в механической системе тел. Как видите, именно полная энергия остается постоянной. Для тела, двигающегося в поле тяжести, формула записывается так: Е = mv2/2 + mgh = const. Не будь на свете трения и сопротивления воздуха, вершины русской горки можно было бы все расположить на одной высоте и взлетать на них сколько угодно раз. Соедините такие идеальные вершины в кольцо — и на них можно было бы пуститься в вечный безостановочный галоп. Но в реальных условиях часть кинетической энергии в пути безвозвратно теряется — расходуется на работу против сил трения. Поэтому вершины горки приходится устраивать «мал мала меньше» и в конце концов с огорчением вылезать из остановившейся тележки. Вечное движение естьСуществует ли вечное движение? Все кругом движется: атомы, пылинки, люди, планеты, звезды. Движение неуничтожимо. Очень легко себе представить вечное движение (во всяком случае, практически вечное) и в какой-нибудь сравнительно небольшой системе тел. Тот же маятник, если исключить трение в точке подвеса, качался бы в безвоздушном пространстве сколь угодно долго. В вечном неутихающем движении вращается Земля вокруг Солнца. И электроны вечно несутся вокруг атомного ядра. И еще физики научились устраивать в своих лабораториях вечные электрические токи, которые кружат в кольцах из особых материалов — сверхпроводников. Словом, вечное движение налицо. Оно и в большом и в малом. А вот вечного двигателя — какого-нибудь автомобиля, который ехал бы, не тратя бензина, — нет. Пресловутый перпетуум-мобиле построить невозможно. Немецкий ученый Герман Гельмгольц в конце прошлого века во всеуслышание заявил об этом и вызвал ропот недовольства среди бесчисленных самоучек-изобретателей. Сколько ведь предлагалось проектов перпетуум-мобиле! Десятки тысяч! До сих пор научные институты и редакции журналов получают чертежи и расчеты «новейших конструкций» вечного двигателя, который, по уверениям авторов, обязательно будет работать, дайте только денег и материалов на постройку. Но, как и предсказал Гельмгольц, на многие тысячи проектов — ни одной действующей машины. А причина проста до удивления. Вся беда в том, что вечный двигатель, по замыслу изобретателей, должен работать — действовать, что-то двигать, а значит, совершать работу. Вечного двигателя нетМожет быть, на вашем жизненном пути встретится страдалец, одержимый мечтой о вечном двигателе. Допустим даже, что он добился невероятного успеха, сумел-таки построить машину, в которой происходит вечное движение: вроде маятника, полностью освобожденного от трения, или такого же колеса, или сверхпроводящего кольца с постоянным неослабевающим током. И вот на столе у него под стеклянным колпаком что-то крутится или раскачивается- Когда-то давно он привел их в движение. И — о радость! — проходит месяц, гол, два года — движение не утихает! Все. что крутилось, крутится, все, что качалось, качается. Страдалец выглядит счастливцем. Он думает, сделано великое дело. Как вылечить его от навязчивой идеи, как растолковать ему, что он неправ? На это надежд мало: склонность к изобретению перпетуум-мобиле похожа на помешательство. Все же скажите ему: вечный двигатель, по самой сути своей, должен не только вертеться. Он еще обязан что-то двигать, исполнять работу, то есть прикладывать какую-то силу на каком-то пути. Иначе он не будет двигателем. Но чтобы работать, хочешь не хочешь, надо тратить энергию. Откуда взять ее? Есть единственная возможность — извлечь ее из добытого с таким трудом вечного движения. А тогда движение перестанет быть вечным — оно отдаст свою энергию и прекратится. Остановится колесо, замрет маятник, исчезнет ток. И никаким чародейством их не возродить. Для восстановления вечного движения придется вложить энергии не меньше, чем было ее взято для исполнения двигателем работы. Выигрыша нет. Так что наш изобретатель ни при каких условиях не сможет использовать свое вечное движение для устройства вечного двигателя. И будет он, бедняга, жаловаться на судьбу, проклинать законы Ньютона, пытаться их «исправить», так чтобы невозможное стало возможным. Как ни печально, и сегодня есть подобные маньяки. Правда, не столь удачливые, как вышеописанный гипотетический страдалец, ибо настоящим изобретателям перпетуум-мобиле еще ни разу не удалось получить в своих машинах даже неработающее вечное движение- Эту диковинную штуку устраивают ученые-физики, которые отлично осведомлены о невозможности вечного двигателя. Фундамент природыВ середине XIX века наука поднялась так высоко, что смогла сформулировать закон сохранения энергии не только для механических, но и для тепловых, химических, биологических природных явлений. Немецкий врач Юлий Роберт Майер посвятил этому свою тяжелую, трагическую жизнь, в которой были и преследования, и сумасшедший дом, и попытки к самоубийству. Физиолог и физик Герман Гельмгольц утвердил всеобщий принцип сохранения энергии теоретически. Английский пивовар Джоуль дал ему первые экспериментальные доказательства. Именно невозможность уничтожить бесследно любой вид энергии и сотворить его из ничего останавливает тележку на русских горках, налагает запрет на перпетуум-мобиле и держит в строжайших рамках все движения, превращения и перемены состояния. Все, а не одни лишь механические, как было у Ньютона. Кроме двигающихся камней, водяных струй, машинных колес в нашем мире трудятся и тепло пара в котле, и огонь костров, и удары молнии, и грохот грома. Совершаются разные формы работы, возникают разные формы энергии: световая, тепловая, звуковая, химическая, электрическая, магнитная. Создав лампы и паровые машины, изобретя порох и электромотор, люди научились превращать энергии друг в друга: тепло горящего угля в движение паровоза, химическую реакцию батарейки в электрический ток и т. д. Чтобы запасать топливо в дорогу, рассчитывать работоспособность электростанций, мощность батарей — для тысяч целей потребовалось знать, как энергия преобразуется из одного вида в другой. И это стало возможно благодаря установлению всеобщего закона сохранения энергии при переходах ее из одного вида в другой. Физики занялись делом, сходным с исследованиями сообразительной мамы Монтигомо—Ястребиного Когтя из притчи Фейнмана, когда эта мама, разыскивая пропавшие кубики, измеряла повышение уровня воды в баке стиральной машины. Надо было измерить и вычислить, сколько тепловой энергии нужно переделать в механическую, чтобы поднять килограммовую гирю на метровую высоту, сколько электрической энергии превратить в тепло, чтобы нагреть литр воды на один градус, и т. д. Все эти данные, извлеченные из бесчисленных экспериментов, занесены в справочники и энциклопедии. Без них не может обойтись ни наука, ни индустрия. В наши дни закон сохранения энергии подтвержден для любых процессов. Двадцатый век присоединил к числу его подданных мощнейшую атомную энергию. Нет ни одного явления, где он нарушался бы, хоть и были случаи, когда некоторых ученых брало сомнение в его универсальности. Ныне сомнения отброшены. Закон сохранения энергии — наиболее широкий из всех физических законов, он связывает самые разобщенные, казалось бы, события. Если бы он нарушился (что, конечно, невозможно), разразилась бы катастрофа, мир перевернулся бы, взорвался, сошел бы с ума! Если исчезнет удивительностьСейчас мы устроим такую катастрофу минимальными средствами, правда жульническую — с участием потусторонней нечистой силы. Сперва оглянемся назад. В этой книжке мы бежим от удивления падению. Хотим понять, почему с равной быстротой падают песчинка и жернов. Причина отыскана в конце второй главы: равенство тяжелой и инертной масс. Это была заметная веха в нашем бегстве. Однако объяснение показалось слишком формальным. Мы побежали дальше. По дороге заглянули в астрономию — взвесили Землю и Солнце, завернули в геофизику — раскопали клад золота, сделали солидный крюк в учение об энергии, где занялись забиванием гвоздя и разговорами о вечных движениях. Зачем это нам понадобилось? Затем, чтобы набраться эрудиции, а главное, чтобы понять, как тесно связано свойство падения со всем миром, со всеми его законами. Это-то сейчас зримо раскроется в катастрофе, которую, по нашей воле, намеревается совершить сам дьявол. Слушайте, какое он делает предисловие: Все эти удивления, смею вас уверить, сплошная чепуха. Зачем удивляться? Зачем мучить себя бегством от удивлений? Надо уметь жить без тревог. Неужели вам не надоела возня с песчинками, жерновами и вечными двигателями? Куда приятнее не думать о них, а сыграть с приятелями в подкидного дурака... Но мир-то, — говорю я, — он удивителен! Пустяки, — отвечает мой собеседник, почесывая рог.— Я так забочусь о вашем покое, что за одну минуту переделаю мир в совсем не странный, в привычный и обыкновенный. Чтобы не было никаких удивлений. Стойте, стойте! — кричу я, чувствуя, что он может натворить недоброе.— Не надо! Пусть мир останется по-прежнему удивительным! Нет, надо! — отвечает он, и злобный огонь светится в его глазках.— Надо! — И он хлопает в ладоши, топает копытом и нехорошим, замогильным голосом орет: — Да сгинет удивительность падения! Приказываю тяжелым телам падать быстрее легких! Пусть падающие жернова обгоняют песчинки, а большие сосульки оставляют позади маленькие, когда падают. Да будет так, как человеку кажется естественным. Ну, а остальное пускай пока остается по-прежнему. Пока!.. В этот момент раздается шум. Я вижу в окно: разламываются дома, рушатся деревья, а облака, крутясь и распадаясь, смешиваются с землей. Звенят стекла, подо мной проваливается пол... Охо-хо! — грохочет сатанинский голос.— Теперь вы не будете удивляться!.. Катастрофа в паркеНезадолго перед этим две подружки, храбрая Аня и робкая Таня, гуляли в Измайловском парке. Они беседовали о том о сем, а потом решили покататься на русских горках. Здорово! — восклицала Аня, когда тележка катилась вниз. Только немножко страшно! — говорила Таня и прижималась к подруге. Не трусь! — подбадривала Аня. И когда тележка поднималась, осмелевшая Таня отстранялась, чтобы, однако, вновь прильнуть к Ане на очередном спуске. Обратите внимание на подчеркнутые слова. В них — суть. Вдруг все вокруг неуловимо переменилось (это был тот самый момент, когда мой рогатый собеседник лишил мир удивительности и приказал тяжелым телам падать быстрее легких). Тележка полетела вниз гораздо стремительнее, чем раньше. Таня испугалась пуще прежнего, теснее прижалась к Ане. Из-за этого тележка помчалась еще скорее, потому что Аня и Таня, соединенные вместе, стали тяжелее, чем каждая по отдельности. Ведь обнявшись, они падали бы с большим ускорением, чем порознь. Так невесть откуда появилась у тележки дополнительная кинетическая энергия. Нарушился закон сохранения энергии! Несколько взлетов — и тележка вознеслась в небо, порвала оковы земного тяготения, устремилась куда-то в. сторону Луны. Печальна судьба Ани и Тани! Быть может, убедительнее цирковой пример. Двое акробатов прыгают на батуте. С некоторой высоты они падают в обнимку, а, оттолкнувшись от упругой сетки, летят вверх порознь. После дьявольского приказа ускорение падения циркачей будет больше, чем замедление подъема — в нервам, случае тяжелая масса акробатов увеличена за счет инертной, во втором, наоборот, инертная увеличена за счет тяжелой. Каждое падение быстрее, чем подъем. При каждом падении акробаты получают прибавку конечной скорости, следовательно, и кинетической энергии. Значит, каждый подъем выше, чем предыдущий. Попрыгав таким образом, циркачи пробивают купол и улетают к звездам. Похожие невероятные события в мире, «лишенном удивительности», произошли повсюду. Везде нарушился закон сохранения энергии, воцарился хаос. Природа буйствовала. Планеты сошли со своих путей, звезды разбрызгали свое вещество. Вселенная взорвалась, погибла! Все это я смог вам описать только потому, что на самом деле ничего подобного не было. Да и не могло быть, несмотря на колдовское могущество сатаны[5]. Ибо никаким чудодейством нельзя лишить природу ее неисчерпаемой удивительности. Примечания:1 Потому-то с глубокой древности начала развиваться статика— область физики, занимающаяся всякого рода неподвижностями: уравновешенными весами, блоками, рычагами. Все это вещи нужные, понимать их важно и полезно, недаром им посвятил много времени прославленный грек Архимед. Даже в неподвижности он подметил многое, что необходимо изобретателям всевозможных машин. Тем не менее, если быть придирчивым, это еще не была настоящая физика. Это была только подготовка к ней. А подлинная физика началась с изучения движений. 2 Кое-кто из современных историков науки ставит под сомнение рассказы первых биографов Галилея о его широких экспериментах. Сведения об этих опытах (вплоть до эпизодов с Пизанской башней) считают вымыслом восторженных учеников великого итальянца. Однако главенствует сегодня точка зрения, разделенная в этой книжке. Она провозглашает Галилея достоверным основателем именно экспериментальной физики. 3 Хоть, честно говоря, и не очень строг. В нем предполагается, что соединение разных тел сопровождается простым арифметическим сложением их весов, а это верно лишь в нашем мире, мире больших тел и не очень больших сил. В микромире иногда дело обстоит сложнее — в своем месте об этом будет сказано. 4 Под таким заголовком у нас издается многотомный курс общей физики, читанный Фейнманом в одном из американских институтов (изд. «Мир», 1965—1967 гг.). 5 Честно говоря, изложенный преступный «мысленный эксперимент» довольно искусствен: кроме непропорциональности тяжелой и инертной масс, он требует сохранения их суммы. В силу привнесения этого дополнительного предположения, нельзя утверждать, что пропорциональность тяжелой и инертной масс есть следствие одного лишь закона сохранения энергии. В рамках классики эта пропорциональность — непонятная случайность. |
|
|||
|
Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх |
||||
|
|
||||