|
||||
Глава 5. Головоломки для умников и умницГоловоломки – одни из самых интересных игр, требующие проявления находчивости, смекалки, оригинальности мышления и умения критически оценить условия или постановку вопроса. Вы можете играть в одиночестве или устроить веселые соревнования с друзьями. Головоломки с цифрамиСумма цифрВ эту игру следует играть вдвоем. Игра довольно сложная, но, если придерживаться правильной тактики, можно без труда одержать победу над соперником. Условие Для игры вам следует выбрать многозначное число, например 999, вычислить сумму его цифр (27), а затем уже приступить к соревнованию. Первый игрок называет число от 27 до 999 (27 называть можно, 999 – нельзя). У выбранного числа следует вычислить сумму цифр, после чего второй игрок должен назвать число, которое меньше названного, но не меньше суммы его цифр и т. д. Проигрывает тот, кто не может назвать следующее число.
Подсказка Попробуйте решить задачу с конца. Для этого рассмотрите текущее число (первоначальное или только что названное соперником), на которое нужно назвать свое число. Однозначные числа всегда проигрышны, поскольку нельзя сделать ход по правилам. А вот числа от 10 до 18 – выигрышны, так как можно назвать однозначное число. Проигрышным является и число 19, поскольку приходится называть число от 10 до 18, и соперник выигрывает. Решение Рассмотрим текущее число (первоначальное или только что названное соперником), на которое нужно назвать свое число. Как уже отмечалось выше, однозначные числа являются проигрышными, поскольку нельзя сделать ход по правилам, а числа от 10 до 18 выигрышны, так как можно назвать однозначное число. Число 19 тоже проигрышное. Выигрышными являются числа от 20 до 298 (можно назвать число 19), а число 299 проигрышное (наименьшее число, имеющее сумму цифр 19 + 1, – это 20. Следующим проигрышным числом является то, что определяется как наименьшее, имеющее сумму цифр 299 + 1, то есть 300. Учитывая все отмеченное выше, чтобы выигрыть, нужно назвать числа 299, 19 или 9. В этом случае соперник не выиграет. Суперкрестики-ноликиВы знаете простую игру в крестики-нолики? Если да, то вы без труда освоите и ее усложненный вариант. Прежде чем начать игру, вам следует начертить на листке бумаги в клетку поле 5 x 5.
На игровом поле игроки ста вят по очереди в любую клетку крестик или нолик. Тот, кому удалось поставить три одинаковых знака в ряд (по горизонтали, вертикали или диагонали), побеждает. Если это не удалось никому из игроков, игра считается сыгранной в ничью. Бесконечная играЭто достаточно сложная игра, больше подходящая для проведения математических олимпиад. Однако, если вы обладаете незаурядными математическими способностями и можете найти достойного соперника, вы интересно и с пользой проведете время. Игроки ходят по очереди. Один называет два числа, являющиеся концами отрезка. Соперник называет два других числа, являющиеся концами отрезка, вложенного в предыдущий. Игра может продолжаться бесконечно долго. Условие
Первый игрок стремится, чтобы в пересечении всех названных отрезков было хотя бы одно рациональное число, а противник старается ему помешать. Решение Чтобы выиграть в эту игру, следует соблюдать правильную стратегию. Первым своим ходом необходимо выбрать такой отрезок, чтобы в нем не было ни одной целой точки вида g/2, где g – целое число. Соблюдая такую стратегию, на n-ом ходу следует выбрать такой отрезок, чтобы в нем не было ни одной точки вида g/n, где g – целое число. При любой игре соперника вы можете выбирать отрезки согласно изложенным выше правилам. А теперь попробуем доказать, что в пересечении всех названных отрезков не может быть ни одного рационального числа. Итак, пусть рациональное число s/d (для некоторого целого числа s и натурального числа d) лежит в пересечении всех отрезков. Но это противоречит тому, что игрок на d-ом ходу назвал отрезок, не содержащий рациональных чисел, представленных в виде дроби со знаменателем d. Синие и зеленые точкиЭта игра довольно сложная. В нее следует играть вдвоем. Для игры потребуется лист бумаги, а также ручки с синим и зеленым стержнями. Условие Игроки ходят по очереди. Первый ставит на листе бумаги зеленую точку, второй ставит на свободные места 10 синих точек. После этого первый игрок опять ставит на свободное место зеленую точку, второй ставит на свободные места 10 синих точек и т. д.
Первый игрок считается победителем, если 3 зеленые точки образуют правильный треугольник. Если второй ему помешает, то, соответственно, выигрывает он. Решение Предположим, первый игрок ставит точки на одной прямой, заботясь только о том, чтобы не попасть в уже поставленную точку (это всегда возможно, поскольку на прямой бесконечно много точек). Если уже поставлено s зеленых точек на прямой, прибавление еще одной точки на этой прямой только увеличивает количество мест, на которые можно поставить зеленую точку так, чтобы с уже поставленными она образовала правильный треугольник. Итак, число мест, куда можно поставить точку, чтобы получился правильный треугольник, после постановки (s + 1) – й зеленой точки равно сумме арифметической прогрессии 2 + 4 + 6 + ... + 2s = s(s + 1). Число синих точек после этого хода станет равным 10(s + 1), что при s > 10 уже меньше, чем число возможных мест для зеленой точки, создающей правильный треугольник. Учитывая все сказанное выше, можно сделать вывод, что у первого игрока всегда есть возможность после 10-го хода одержать победу. Угадывание чиселЭто очень сложная головоломка, в которую следует играть вдвоем. При этом соперники должны обладать математическими способностями и определенными знаниями. Условие Один из игроков задумывает 10 натуральных чисел: sp s2, s3, s10. Соперник старается угадать их, задавая определенные вопросы. Разрешается задавать вопросы следующего типа: чему равна сумма b1s1 + b2s2 + ... + b10s10, где b1, b2, b10 – некоторые натуральные числа? При этом угадать задуманные числа следует не более, чем за 5 вопросов. Решение Выяснить, какие числа загадал соперник, вы можете всего за два вопроса. За первый вопрос следует узнать значение выражения s1 + s2 + s3 + ... + s10. Предположим, что оно равно m. Возьмем достаточно большое число n, такое, что 10n > m. Задав второй вопрос, нужно узнать значение выражения s1 + 10ns2 + 102ns3 + ... + 109ns10.
Если значение этого выражения равно г, то в десятичной записи числа г справа налево будут идти группы из n-цифр, дающие десятичные записи чисел s1, s2, s3, s10, возможно с несколькими нулями впереди (поскольку s1, s2, s3, s10 < 10n, при сложении чисел s1, 10ns2, 102ns3, 109ns10 в столбик переносов не возникает). Вычеркивание чиселВ эту игру следует играть вдвоем. Как и в предыдущей игре, соперникам нужны определенные знания математики. Условие Игроки по очереди вычеркивают 9 чисел (по своему выбору) из последовательности 1, 2,100, 101. После одиннадцати таких вычеркиваний останутся 2 числа. Первому игроку присуждается столько очков, какова разница между этими оставшимися числами.
Решение Первым ходом вам следует вычеркнуть 9 чисел от 47 до 55. Остальные числа разбиваются на пары: 1 – 56, 2 – 57, 46 – 101. После каждого хода соперника, вам нужно вычеркнуть числа таким образом, чтобы в каждой паре было вычеркнуто или оба числа, или ни одного. Таким образом, в конце останется пара чисел, разность которых равна 55. Это самое большое количество очков, которое можно получить в этой игре. Простые игры-головоломкиВ такие игры могут играть даже дети. Тем не менее они интересны и взрослым. Для большинства таких игр вам потребуются листы бумаги и ручки. Собаки и кошкиВ эту игру следует играть вдвоем. Первый игрок задумывает любое четырехзначное число, содержащие разные цифры. Соперник старается угадать это число. При каждом ходе отгадывающий называет четырехзначное число с разными цифрами. Если цифра из названного числа присутствует в отгадываемом числе, такая ситуация называется «собака». Если же цифра из названного числа есть в отгадываемом числе и стоит на том же самом месте, такая ситуация называется «кошка». Предположим, первый игрок задумал число 5732, а его соперник назвал число 3798. Первый игрок должен сказать противнику: «Одна кошка и одна собака». Второй в свою очередь запоминает это или записывает на листке бумаги. Свое число задумывает каждый из игроков. Они ходят по очереди. Выигрывает тот, кто раньше отгадает число соперника. Морской бойЦель этой игры – уничтожить объекты (корабли) противника. Играют в «морской бой» вдвоем. Каждому из игроков следует начертить по два квадратных поля размером 10 х 10 клеток и нарисовать на одном из них корабли (рис. 1).  Рис. 1. Вооруженные силы каждого игрока должны содержать следующие объекты: – четыре однопалубных корабля (1 клетка); – два двухпалубных корабля (2 клетки); – два трехпалубных корабля (3 клетки); – один четырехпалубный корабль (4 клетки). Корабли нельзя располагать вплотную друг к другу, то есть между двумя соседними объектами должна быть как минимум одна свободная клетка. Вы выбираете клетку, называете ее координаты и «стреляете» в этот квадрат. Если вы потопили корабль противника, последний должен сказать: «Убил». Если вы ранили корабль (то есть попали в объект, имеющий больше чем одну палубу), то соперник должен сказать: «Ранил». В случае попадания в корабль соперника вы получаете дополнительный ход. Игра заканчиваеся, когда один из ее участников теряет все корабли. Морской бой по-английскиВ эту игру, как и в традиционный морской бой, играют вдвоем. Каждому игроку сначала нужно начертить два квадратных поля размером 10 х 10 клеток и нарисовать такое же количество кораблей, как и в предыдущей игре. После этого один из игроков называет сразу несколько (от 3 до 10, по уговору) координат клеток на поле противника. Последний сообщает нападающему, сколько попаданий произошло, однако не указывает, на каких делениях находятся убитые или раненые корабли, а затем сам делает ход. С каждым ходом соперников уменьшается количество уцелевших кораблей. Победа присуждается самому меткому игроку. Морской бой по-американскиКаждый игрок чертит два игровых поля размером 22 х 14 клеток, после чего делят их по-полам – на море и сушу. На море располагаются такие же объекты, как и в традиционном морском бое, а на суше игроки рисуют четыре танка (по 1 клетке) и четыре самолета (по 4 клетки). Игру проводят по тем же правилам, что и традиционный морской бой.
Бой канонерокЭто еще один из вариантов «Морского боя». Каждый из игроков чертит два поля размером 10 х 10 клеток и, как в традиционной игре, рисует на одном из них боевые единицы – корабли, которые состоят из одной клетки. Игра проводится по правилам обычного морского боя. Летучий голландецВ этой игре, в отличие от традиционного морского боя, фигурирует только один многопалубный (8 клеток) корабль. Игроки рисуют по два игровых поля размером 20 х 20 клеток. Корабль должен занимать несколько клеток по горизонтали, вертикали и диагонали. Противники ходят по очереди. Если кто-нибудь из них попадает в палубу корабля соперника, последний имеет право передвинуть своего «летучего голландца» на любое другое свободное место своего игрового поля. При этом корабль теряет затонувшую палубу, но его контур остается прежним. ВиселицаЭто популярная игра-головоломка, созданная специально для двух игроков. Для нее вам понадобятся чистый лист бумаги и ручка (карандаш). Один из игроков задумывает слово. При этом он должен быть уверен, что его соперник знает это слово и знаком с его правильным написанием. На листке бумаги он пишет первую и последнюю букву этого слова, а вместо остальных букв ставит звездочки или точки. Например, г*******а (гильотина). Соперник называет любую букву, которая, по его мнению, входит в состав этого слова. Если такая буква в слове есть, другой игрок вписывает ее вместо звездочки (если таких букв две, три и более, он вписывает их все). Если буква отсутствует в этом слове, он рисует первую деталь виселицы. Противник продолжает называть буквы до тех пор, пока не отгадает все слово. За каждый неправильный ответ первый игрок рисует по очереди все детали виселицы, а затем части туловища повешенного. Если туловище нарисовано раньше, чем противник угадывает слово, первый игрок побеждает. Если его соперник отгадывает слово правильно до того, как детали виселицы и туловище нарисовано полностью, побеждает он, и тогда наступает его очередь задумывать слово. КоридорчикиДля этой игры вам понадобятся лист бумаги в клетку прямоугольной или квадратной формы. Игроки по очереди проводят вертикальные или горизонтальные линии в одну клетку. Тот, кому удалось замкнуть линиями клетку, ставит в ней крестик (нолик) и получает еще один ход. Когда все клетки окажутся занятыми, подсчитывают, кто из игроков захватил больше клеток. Головоломки со взвешиваниемВ такие игры вы можете играть как в одиночестве, так и в компании друзей, предложив им решить одну из головоломок за определенное время. Выигрывает тот, кто первым правильно решит задачу. Фальшивые монетыУсловие На столе лежит десять пронумерованных коробочек. В каждой из них лежит по десять монет. В одной из коробочек находятся фальшивые монеты. Настоящая монета весит 10 г, а поддельная – 9. В помощь даны весы со шкалой в граммах. Как определить, в какой коробочке находятся фальшивые монеты, используя весы только для одного взвешивания? Весы могут взвешивать не более 750 г. Ответ Возьмем из первой коробочки одну монету, из второй две, из третьей три и т. д. Всего получается 55 монет, общий вес которых должен быть 550 г. Но так как среди них есть фальшивые, то показанный весами вес будет отличаться от 550 г на номер коробочки с фальшивыми монетами. Другими словами, если весы покажут 544 г, то фальшивые монеты в шестой коробочке: 550–544 = 6.
ПленникиУсловие Граф, графиня и их дочь находятся в темнице высокой башни. Они весят 80, 42 и 36 кг соответственно. Еду им поднимали в двух больших корзинах, прикрепленных к концам длинной и прочной веревки, которая была перекинута через балку, вбитую под самой крышей. Однажды получилось так, что, когда одна корзина находилась на земле, другая была на уровне окна в камере пленников. Эти корзины стали единственной надеждой на спасение. Разумеется, когда одна корзина становилась тяжелее другой, она опускалась. Но если разница в весе превышает 6 кг, корзина опускалась вниз. Единственное, что может помочь пленникам бежать из замка, это находящееся в их камере пушечное ядро весом 30 кг. Попробуйте, используя пушечное ядро как противовес, помочь пленникам очутиться на свободе. Ответ Сначала спускается дочь, используя пушечное ядро в качестве противовеса. Достигнув земли, она не вылезает из корзины. Графиня занимает место ядра и спускается вниз, используя дочь в качестве противовеса. Затем дочь поднимается вверх и вместе с графом кладет в корзину ядро. В опустившуюся корзину вместе с ядром садится графиня, что позволяет графу опуститься на землю. Когда он оказывается внизу, графиня с ядром поднимается наверх, она вылезает, а корзина с ядром опускается вниз. В пустую корзину наверху садится дочь и спускается на землю. Графиня вытаскивает ядро из поднявшейся корзины и спускается вниз, используя дочь как противовес. Дочь кладет в пустую корзину ядро, а сама садится в поднявшуюся корзину и спускается, используя ядро в качестве противовеса. Кофе в коробкахУсловие Как развесить 20 кг кофе в 10 коробок по 2 кг в каждой за девять взвешиваний, имея только гири весом по 5 и 9 кг и используя большие весы с двумя чашами? Ответ На одну чашу весов следует положить гирю весом 5 кг, на другую – гирю весом 9 кг. После этого нужно уравновесить весы, насыпав 4 кг кофе в чашу с гирей 5 кг. Затем необходимо убрать гири с чаш весов, оставить 4 кг кофе в одной чаше и уравновесит весы, насыпав во вторую чашу еще 4 кг кофе. После этого следует отвесить еще 4 кг кофе, а затем еще 4 кг и еще 4 кг. Таким образом, после четырех взвешиваний в остатке будет тоже 4 кг кофе. Их нужно разделить пополам, уравновесив чаши весов. Серебро и медьУсловие Имеется 100 серебряных монет разных размеров и 101 медная монеты также разных размеров. Если у одной монеты размер больше, чем у другой, то она весит больше, но это верно только для монет, изготовленных из одного и того же металла. Все монеты можно легко упорядочить по размерам на глаз. Разумеется, отличить серебро от меди тоже можно. Как за восемь взвешиваний определить, какая монета из всех занимает по весу 101-е место? Решая головоломку, следует помнить, что все монеты различаются не только по размеру, но и по весу. Ответ Сначала все монеты следует выложить в два ряда в порядке возрастания размера: медные отдельно, серебряные отдельно. Пусть первая по счету в каждом ряду монета самая большая и тяжелая. Среднюю по весу монету можно найти, одну за другой взвешивая средние монеты каждого ряда. Сначала нужно взвесить 51-ю медную монету и 50-ю серебряную. Если первая тяжелее, то искомая монета находится среди 52-101-й медной и 51-100-й серебряной, то есть 51 + 50 монет. Остальные монеты можно отложить. После этого следует снова взвесить средние монеты. Поскольку число вариантов растет в геометрической прогрессии, мы рассмотрим только итоги. Из 51 + 50 монет нужно выбрать и сравнить 25-ю и 26-ю монеты. Остается 26 + 25 монет. Затем необходимо взвесить 13-ю монету каждого ряда. Остается 13 + 13 или 13 + 12 монет. Далее мы рассмотрим только случай 13 + 13 и 13 + 12 аналогично. После этого надо взвесить 7-ю монету каждого ряда. Остается 7 + 7 монет. Затем – 4-ю и 3-ю монеты каждого ряда. Остается 4 + 3 монеты. Предположим, что остались медные монеты А, В,С,Би серебряные X, Y, Z (все в порядке возрастания). Следует взвесить монеты В и Y. Если В > Y, то средняя по весу монета – это одна из C, D, X, Y, если нет, то это одна из А, В, Z. В первом случае нужно взвесить монеты С и Y. Какая из них больше, та и искомая. Если же С > Х, следует взвесить монеты D и Х: какая из них больше, та и искомая. Пиво на троихУсловие Три человека купили сосуд, полностью заполненный 24 л пива. Потом они приобрели три пустых сосуда объемом 5, 11 и 13 л. Как им поделить пиво на равные части за пять переливаний, используя только эти четыре сосуда? Ответ Как видно из условия, сосуды могут содержать 24, 13, 11 и 5 л пива. Их начальное состояние: 24, 0, 0 и 0 л пива. Решение: 1– е переливание – 8, 0, 11, 5; 2– е перливание – 8, 11, 0, 5; 3– е переливание – 8, 13, 3, 0; 4– е переливание – 8, 8, 3, 5; 5– е переливание – 8, 8, 8, 0. Вино на двоихДва человека купили 8 ведер вина, налитого в большой бочонок. У них имеется еще два пустых бочонка, вместимостью 5 ведер и 3 ведра. Как им разделить вино поровну, пользуясь только этими тремя бочонками? Ответ Как видно из условия, имеется три бочонка вместимостью 8, 5 и 3 ведра. Их начальное состояние: 8, 0 и 0 л вина. Разделить вино можно двумя способами. Способ 1-й: 1– е переливание – 3, 5, 0; 2– е переливание – 3, 2, 3; 3– е переливание – 6, 2, 0; 4– е переливание – 6, 0, 2; 5– е переливание – 1, 5, 2; 6– е переливание – 1, 4, 3; 7– е переливание – 4, 4, 0. Способ 2-й: 1– е переливание – 5, 0, 3; 2– е переливание – 5, 3, 0; 3– е переливание – 2, 3, 3; 4– е переливание – 2, 5, 1; 5– е переливание – 7, 0, 1; 6– е переливание – 7, 1, 0; 7– е переливание – 4, 1, 3; 8– е переливание – 4, 4, 0. Три литра компотаУсловие Имеются трехлитровая банка компота и две пустые банки: одна – литровая, другая – двухлитровая. Как разлить компот так, чтобы во всех трех банках было по одному литру? Ответ Способ 1-й: наполнить литровую банку, вылить ее содержимое в двухлитровую банку, наполнить литровую банку из трехлитровой банки. Способ 2-й: наполнить двухлитровую банку, наполнить из нее литровую банку. РазрезаниеЭто очень интересные геометрические головоломки, которые интересны и детям, и взрослым. Их можно разгадывать как в одиночку, так и в компании. Квадрат из крестаУсловие Разрежьте крест (рис. 2) на четыре равные части и сложите из них квадрат. При этом высота и ширина квадрата должны быть такими же, как высота и ширина креста. 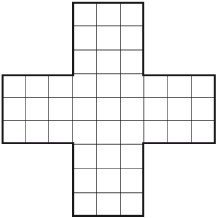 Рис. 2. Ответ Сначала следует разрезать крест так, как показано на рисунке 3, а затем из полученных частей, «вывернув их наизнанку», сложить квадрат, который будет иметь отверстие в середине (рис. 4). 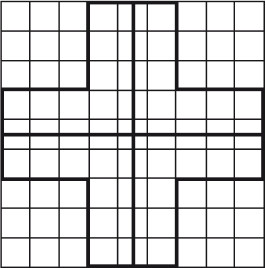 Рис. 3. 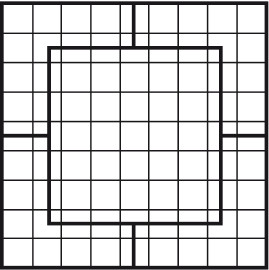 Рис. 4. Доска с отверстиемУсловие Распилите квадратную доску с отверстием у одного из углов (рис. 5) на минимальное количество кусков так, чтобы, сложив их заново, получилась точно такая же доска, но с отверстием, расположенным в центре.  Рис. 5. Ответ Сначала отпилите у доски указанный на рисунке 6 фрагмент и, развернув, приставьте его к правому верхнему углу уменьшенного квадрата.  Рис. 6. 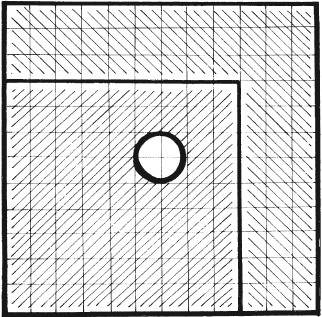 Рис. 7. В результате получится доска исходного размера, но с отверстием в центре (рис. 7).
Восемь частейУсловие Разделите фигуру, приведенную на рисунке 8, на восемь одинаковых частей. 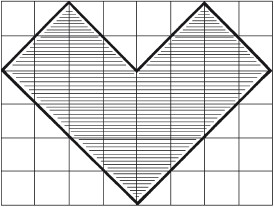 Рис. 8. Ответ Разделить исходную фигуру на восемь одинаковых частей можно так, как показано на рисунке 9. Как получить квадрат из буквы ZУсловие Разрежьте приведенную на рисунке 10 фигуру в виде буквы Z на три части и сложите из них квадрат. Решите головоломку двумя способами.  Рис. 9.  Рис. 10. 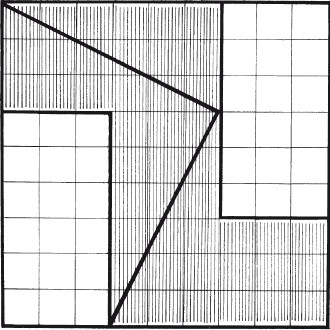 Рис. 11. 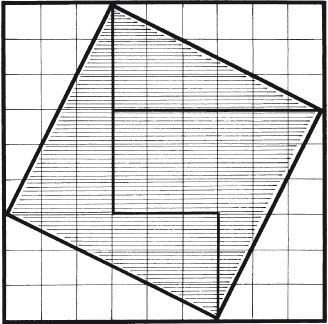 Рис. 12. Ответ Первый способ деления фигуры показан на рисунках 11 и 12. Второй способ деления фигуры показан на рисунках 13 и 14. 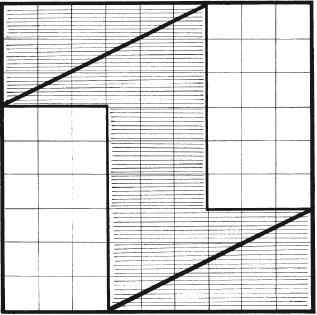 Рис. 13. ТрапецияУсловие Разрежьте трапецию (рис. 15) на четыре равные и одинаковые по форме части, не повторяющие исходную форму. Ответ Разрезать трапецию на четыре части можно так, как показано на рисунке 16. 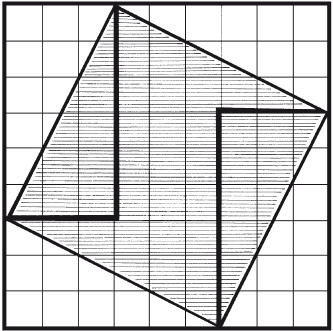 Рис. 14. 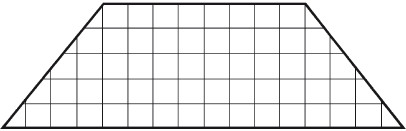 Рис. 15. 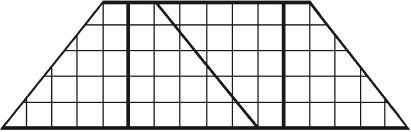 Рис. 16. КвадратУсловие На рисунке 17 представлен квадрат 13 х 13 клеток, состоящий из 169 квадратиков.  Рис. 17. Попробуйте разделить этот большой квадрат на квадраты меньшего размера. При этом линии должны проходить по границам маленьких квадратов. Ответ Разделить большой квадрат можно на одиннадцать меньших квадратов так, как показано на рисунке 18. 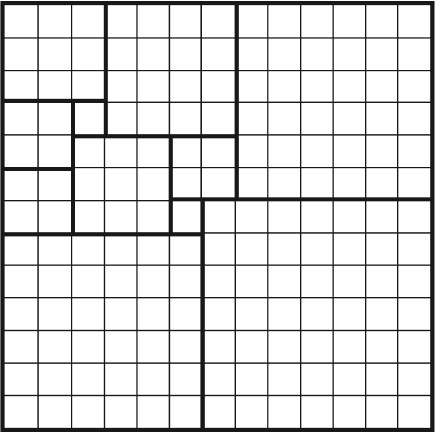 Рис. 18. Пять из двадцати пятиУсловие Заштрихуйте пять квадратов из двадцати пяти на приведенной на рисунке 19 фигуре так, чтобы поделить изображение на пять равных частей одинаковой формы. Решите эту головоломку двумя способами. 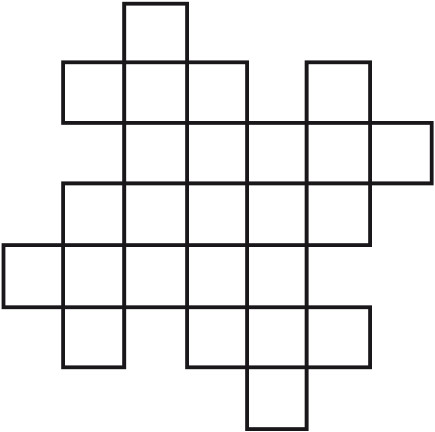 Рис. 19. Ответ Первый способ. На рисунке 20 пять заштрихованных клеток образуют крест, а сама фигура делится еще на четыре таких же креста. Второй способ. На рисунке 21 заштрихованные клетки делят фигуру на пять частей по четыре клетки в каждой.  Рис. 20. 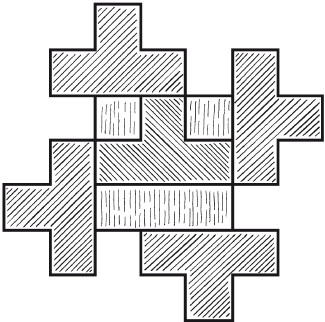 Рис. 21. Завещание помещикаУсловие Помещик завещал принадлежавшие ему 400 га земли и пять домов (рис. 22) своим пятерым сыновьям.  Рис. 22. По завещанию земля делилась следующим образом: – старшему сыну – 200 га; – второму сыну – 100 га; – третьему сыну – 50 га; – четвертому сыну – 25 га; – младшему сыну – 25 га. В условии завещения говорилось, что все наделы земли должны иметь одинаковую форму и на каждом из них должен стоять дом. Помогите сыновьям выполнить волю отца. Ответ Старшему сыну – половину всего участка. Второму – половину от оставшегося. Третьему – половину от оставшегося. Четвертому и младшему – по половине от оставшегося. Таким образом, каждый из сыновей получает участок треугольной формы (рис. 23). 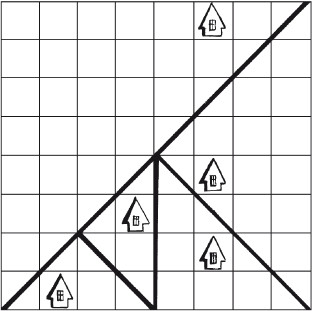 Рис. 23. Деление поляУсловие Разделите поле (рис. 24) размером 12 х 8 квадратов семью прямыми линиями на восемь участков, имеющих одинаковую площадь, так, чтобы на каждом из участков оказалось по два дерева. При этом линии следует проводить только по границам маленьких квадратов.  Рис. 24. Ответ Разделить поле можно так, как показано на рисунке 25. 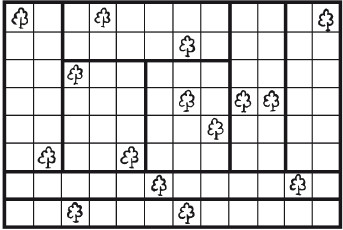 Рис. 25. ОкружностьУсловие На какое максимальное количество частей можно разрезать окружность (рис. 26) четырьмя разрезами? При этом перекладывать части после разрезания нельзя.  Рис. 26. Ответ Окружность можно разрезать на одиннадцать частей так, как показано на рисунке 27.  Рис. 27. ДачникиУсловие Попробуйте разделить поровну земельный участок (рис. 28), не нарушая при этом указанных границ и не трогая дачников так, чтобы все они получили земельные наделы одинакавой формы. 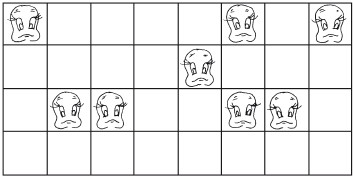 Рис. 28. Ответ Разделить земельный участок между дачниками можно так, как показано на рисунке 29. 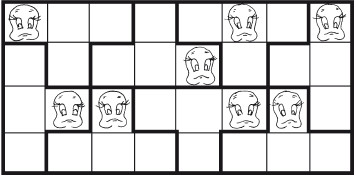 Рис. 29. МногоугольникУсловие Разделите многоугольник, изображенный на рисунке 30, на две равные меньшие фигуры одинаковой формы. 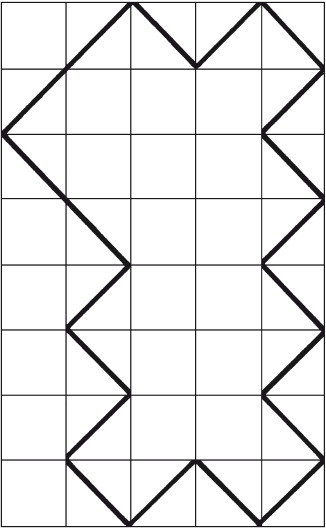 Рис. 30. Ответ Разделить многоугольник на две фигуры одинаковой формы можно так, как показано на рисунке 31. 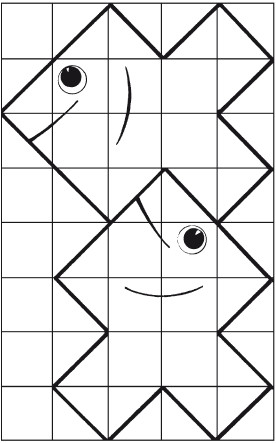 Рис. 31. Праздничный пирогУсловие Квадратный пирог (рис. 32) хотели разрезать на шестнадцать частей, но хозяйка решила разрезать его на шесть квадратных кусков – пять одинаковых и один большой. Можно ли разрезать пирог таким образом? 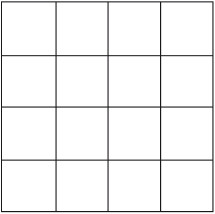 Рис. 32. Ответ Разрезать пирог на шесть кусков можно так, как показано на рисунке 33.  Рис. 33. Задачки для математических викторинЭти игры-задачки больше всего подходят для математических олимпиад, однако вы можете предложить решить их своим друзьям или коллегам, устроив что-то наподобие занимательной викторины. ВаннаУсловие Ванна заполняется холодной водой за 6 минут 40 секунд, горячей – за 8 минут. Если из полной ванны вынуть пробку, вода вытечет за 13 минут 20 секунд. Сколько времени нужно, чтобы наполнить ванну полностью, при условии, что открыты оба крана, но ванна не заткнута пробкой? Ответ Сначала нужно перевести время в секунды: чтобы наполнить ванну холодной водой требуется 400 секунд, значит, за одну секунду наполняется 1/400 часть ванны. Аналогично для горячей воды. За одну секунду наполняется 1/480 часть ванны. Аналогично для спуска воды. За одну секунду выливается 1/800 часть ванны. Примем за общий знаменатель 4800 и запишем уравнение: 12/4800 + 10/4800 – 6/4800 = 16/ 4800= 1/300 Полученная величина равна количеству воды, наливающейся в ванну каждую секунду. Таким образом, потребуется 5 минут, чтобы наполнить ванну полностью. ЩукаУсловие Рыболов поймал щуку, у которой голова была длиной 6 см, хвост размером с голову и половину тушки, а тушка размером с половину длины рыбы с головы до хвоста. Сколько сантиметров щука была в длину? Ответ Голова 6 см, тушка 24 см, хвост 18 см. Длина щуки с головы до хвоста равна 48 см. Диалог о детяхУсловие – Сколько детей у твоей сестры? – Трое. – И сколько им лет? – Если перемножить все три возраста, то получится 36. – Этой информации недостаточно. – В сумме их возраст равен номеру моего дома, и ты его знаешь. – Все равно сведений мало. – Самый старший ребенок любит играть в теннис. – Отлично, теперь я смогу назвать возраст каждого из детей. Какого возраста дети? Ответ Существует восемь комбинаций, когда произведение трех чисел дает 36: 3 х 3 х 4, 1 х 1 х 36, 12 х 3 х 1, 2 х 2 х 9, 6 х 3 х 2, 6 х 6 х 1, 9 х 4 х 1, 18 х 2 х 1. После подсказки о том, что сумма возрастов равна номеру дома, а он известен, информации все равно недостаточно, следовательно такую сумму дают как минимум две комбинации из всех возможных. Единственным числом, которому в сумме равны две комбинации чисел, является 13 (6 + 6 + 1 и 2 + 2 + 9). Последняя подсказка исключает первый вариант, значит возраст детей 2, 2 и 9 лет. Пешеходы и осаУсловие Два города A и B находятся на расстоянии 30 км друг от друга. Из этих городов одновременно выходят друг другу навстречу два пешехода и двигаются, не останавливаясь, каждый со скоростью 5 км/ч. Но вместе с первым пешеходом из города A вылетает оса, пролетающая в час 10 км. Она опережает первого пешехода и летит навстречу второму, вышедшему из города B. Встретив его, она сразу поворачивает назад к пешеходу, двигающемуся из города A. Повстречав его, оса снова летит обратно навстречу второму пешеходу. Она продолжала свои полеты вперед и назад до тех пор, пока пешеходы не встретились. Тогда она успокоилась и села на дерево. Сколько километров пролетела оса? Ответ Оса, не останавливаясь, летела ровно 3 часа, а значит она пролетела 30 км. Многодетная семьяУсловие Сколько детей в многодетной семье, если известно, что у каждого сына сестер столько же, сколько и братьев, а у каждой дочери братьев вдвое больше, чем сестер? Сколько братьев и сестер в многодетной семье? Ответ В многодетной семье 7 детей: 4 сына и 3 дочери. День рождения ИванаУсловие Этому парню по имени Иван не позавидуешь. Вот уже много лет подряд его дед Никита мучает его одним и тем же фокусом. Как только наступает день рождения внука старый скупердяй предлагает ему следующее: дав Ивану десять однодолларовых купюр и десять стодолларовых, он просит разложить их в две одинаковые коробочки. После этого дед завязывает внуку глаза и несколько раз передвигает коробочки по столу – так, чтобы Иван не догадался, где какая. Если внук кладет стодолларовые купюры сверху, вредный старик еще и перемешивает их в коробочке. Затем дед позволяет Ивану вытащить единственную купюру, которая, чаще всего оказывается однодолларовой.
Каким образом Иван может увеличить свои шансы на успех и вытащить стодолларовую купюру? Ответ Ивану следует положить стодолларовую купюру в одну коробочку, а все остальные – в другую, после чего его шансы попасть в коробочку с заветной купюрой оцениваются как 50 на 50. Но, если он запустит руку в коробочку с девятнадцатью купюрами, то его шансы выудить стодолларовую составят 9 из 19. Поэтому в целом вероятность того, что Иван достанет желанную купюру, можно определить так: 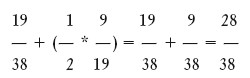 Это означает, что шансы Ивана вытаскивать ежегодно на свой день рождения по стодолларовой купюре равны 0,7368, или примерно 74 %. Звезды балетаУсловие Звезды балета, сестры Ирина и Елена, вовсе не собирались открывать поклонникам свой возраст. Их пресс-секретарь на вопрос репортеров о возрасте сестер сказал следующее: «Если сложить возраст обеих сестер, в сумме получится 44. Сейчас Ирине вдвое больше, чем было Елене, когда Ирине было наполовину столько же, сколько будет Елене, когда она станет вдвое старше, чем была Ирина тогда, когда ей было в три раза больше, чем тогда Елене». Сколько лет сестрам? Ответ Чтобы ответить на этот вопрос, следует начать решение задачи с конца. Когда Елене было 5,5 лет, Ирине было 16,5 лет, когда Елене будет в три раза столько же, то есть 49,5 лет, то, разделив это число пополам, получим 24 и 3/4. Когда Ирине было столько лет, Елене было 13 и 3/4 лет. Следовательно, возраст Ирины в два раза больше, то есть 27,5 лет. Теперь нетрудно узнать возраст другой сестры: 44–27,5 = 16,5. Максимальная суммаУсловие На рисунке 34 числа 1, 18, 17 и 14 стоят в углах воображаемого квадрата и дают в сумме 50. Найдите квадрат (любого размера) с числами, стоящими в его углах, которые давали бы максимальную сумму. 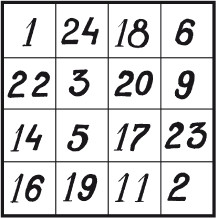 Рис. 34. Ответ Максимальная сумма чисел, находящихся в углах квадрата равна 82 (рис. 35). Попрыгунья-стрекозаУсловие Попрыгунья-стрекоза 1/2 каждых суток лета спала, 1/3 каждых суток танцевала, 1/6 часть – пела. Остальное время она решила посвятить подготовке к зиме. Сколько часов в сутки стрекоза готовилась к зиме? 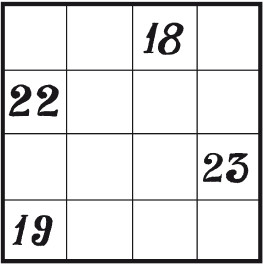 Рис. 35. Ответ На подготовку к зиме у стрекозы не оставалось времени. Разбитый циферблатУсловие Циферблат часов (рис. 36) разбился на четыре части так, что сумма римских чисел на каждом куске стала равняться двадцати. Определите, как треснул циферблат. 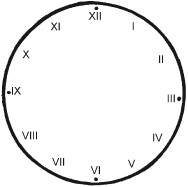 Рис. 36. Ответ Ответ показан на рисунке 37.  Рис. 37. Разбитый циферблат Сумма и произведениеУсловие Назовите состоящие из одинаковых цифр числа, сумма которых равна их произведению. При этом числа должны состоять не менее, чем из двух цифр. Ответ Это числа 11 и 1,1. При сложении и перемножении результат равен 12,1. ТараканыУсловие В углах квадрата со стороной 10 см находится по таракану. Если все четыре насекомых начнут двигаться одновременно и с постоянной скоростью, каждый – по одной из сторон квадрата по направлению к другому таракану (по часовой стрелке), какое расстояние преодолеет каждый из них до того момента, когда тараканы встретятся? При этом следует помнить, что тараканы всегда ползут по кратчайшему пути к своей цели. Для точности следует принять тараканов за безразмерную точку. Ответ В любой момент времени таракан-преследователь ползет по направлению, перпендикулярному пути преследуемого насекомого. По этой причине последнее никак не может оторваться от преследователя или приблизиться к нему. А таракану-преследователю нужно преодолеть лишь те самые 10 см, которые разделяли их в самом начале. Колода картУсловие На столе лежит колода карт, все карты на месте. Игроки по очереди берут из колоды произвольное количество карт, но не более трех. Выигрывает тот, кто забрал из колоды последние карты (или карту).
В одном из розыгрышей победил участник, который ходил первым, причем он был уверен в выигрыше с самого начала. Определите, какая была колода – пикетная (32 карты), средняя (36 карт) или полная (54 карты)? Объясните свой ответ. Ответ Правильная стратегия – всегда оставлять в колоде число карт, кратное четырем. Игрок, который ходит первым, выгрывает в том случае, если в колоде 54 карты. Первым ходом он берет две карты, а затем, если соперник при ходе берет n карт, всегда должен брать 4 – n. Если в колоде 32 или 36 карт, при правильной игре соперника тот участник, который ходит первым, проигрывает. ВыборыУсловие В государстве Заполярное имеется 999 избирательных округов с одинаковым числом избирателей в каждом. От них нужно выбрать по одному депутату. Однако в этой стране всего три партии – партия любителей водки, партия любителей пива и партия любителей безалкогольных напитков. Согласно проведенным социологическим исследованиям, симпатии населения в Заполярном распределились следующим образом: – партия любителей водки (PLV) – 15 % избирателей; – партия любителей пива (PLP) – 30 % избирателей; – партия любителей безалкогольных напитков (PLBN) – 55 % избирателей. Если в первом туре ни один кандидат не набирает 50 % голосов, во второй тур проходят двое, набравшие наибольшее число голосов. Так как сторонников партий PLV и PLP объединяет тяга к спиртному, они всегда поддерживают кандидатов друг друга во втором туре (за исключением случаев, когда оба их кандидата проходят во второй тур). Также во втором туре сторонники партии PLBN всегда голосуют за кандидата от партии PLV, если кандидат от PLBN в этом округе проиграл в первом туре. Оцените, какое наименьшее и какое наибольшее число кандидатов от каждой партии может быть избрано в парламент государства Заполярное. Ответ PLV. Минимальное число кандидатов – 0. Теперь определим максимальное число кандидатов. При выборах в два тура оно будет с минимальным перевесом PLV над PLP в части округов, то есть когда PLV наберет 25 % + 1 человек, PLP – 25 %, а PLBN – 50 % – 1 человек. Тогда во второй тур выйдут PLV и PLBN, и PLV при поддержке PLP выиграет с перевесом в 1 голос. Поскольку PLV имеет 15 % голосов, то 25 % может набрать в 60 % округов, то есть 0,6 х 999 = 599,4 округа. Получается, что PLV может победить максимум в 599 округах. В 600-м округе будет только (0,4 х 0,25) = 0,1 = 10 % избирателей, что недостаточно для прохождения во второй тур, но при достаточно большом числе избирателей в каждом округе должно хватить для обеспечения не 25 %, а 25 % + 1 человек, необходимых для победы в 599 округах. PLP. Минимальное число кандидатов – 0. Как и в предыдущем случае, попробуем определить максимальное число кандидатов. В 599 округах PLP могут победить аналогично PLV, то есть, набрав в первом туре 25 % + 1 голос, а PLV наберут в этих округах ровно 25 % голосов. В остальных округах сторонников PLV практически не останется, зато сторонники PLP будут. Их количество от общего числа избирателей 999 округов (0,30 -0,25 х 599/999) = 0,14989. Чтобы выиграть в части из оставшихся 400 округов, им необходимо набрать там 50 % голосов. Это возможно в округах в количестве (999 х 0,14989/05) = 299,5. Таким образом, PLP может победить в (599 + 299) = 898 округах, после чего останется не-задействовано (0,30 – 0,25 х 599/999 – 0,5 х 299/999) = 0,00045 = 0,045 % избирателей. В одном округе это составило бы 0,045 % х 999 = 44,9 %. Но там может быть только (0,15 х 999 – 0,25 х 599) = 0,1 = 10 % сторонников PLV. В таком случае в этом округе во второй тур выходят PLP и PLBN, и во втором туре PLP при поддержке PLV выигрывает. Получается, что PLP может выиграть в 899 округах. PLBN. Случай с минимальным числом депутатов от PLBN похож на случай с максимальным числом депутатов от PLP. Другими словами, в части округов, где PLBN проигрывают, у нее 50 % – 1 голос, а у PLV и PLP в сумме 50 % + 1 человек. В остальных округах у PLBN 100 % голосов. При этом PLBN победит в 100 округах. Максимальное количество округов, в которых может выиграть эта партия, – 999 (например, при равномерном распределении). Пятьдесят шестьУсловие Получите из четырех пятерок число 56, используя математические знаки действий. Ответ 55 + 5/5 = 56. Страусиные яйцаУсловие Если 1,5 страуса несут 1,5 яйца в 1,5 дня, то сколько яиц снесут 6 страусов за 6 дней? Ответ Получается, что один страус несет 2/3 яйца ежедневно, значит, 6 страусов снесут за день 4 яйца, а за 6 дней – 24 яйца. Наследство пасечникаУсловие После смерти пасечника трем его сыновьям досталась в наследство огромная пасека. Согласно завещанию ульи были разделены между наследниками в такой пропорции: Иван получил на 20 % больше, чем Петр, и на 25 % больше, чем Николай. При этом Петру досталось 3600 ульев. Посчитайте, сколько досталось ульев Николаю и сколько всего ульев получили в наследство сыновья пасечника. Ответ Иван получил 4320 ульев, Петр – 3600, а Николай – 3456. Все наследство составило 11376 ульев. Любители автомобилей NissanУсловие Федор и Валерий обсуждали достоинства новой покупки Валерия – автомобиля Nissan Micra. «Отличное приобретение, – сказал другу Федор, – сколько же теперь у тебя автомобилей?». «Попробуй сам сосчитать, – ответил другу Валерий. – Все модели в моем гараже, кроме двух, Nissan Micra, все, кроме двух, Nissan Almera, все, кроме двух, – Nissan Primera». Посчитайте, сколько всего автомобилей в гараже Валерия. Ответ В гараже Валерия всего три автомобиля: Nissan Micra, Nissan Almera и Nissan Primera. Поставщик банановУсловие Иван Иванович Иванов занимается оптовой продажей бананов. В один из дней, получив заказ от заведений, с которыми он работает, он погрузил в свой грузовик 20 ящиков бананов и отвез клиентам: ресторан «Клубничка» получил на 2 ящика бананов больше, чем кафе «Лакомка»; ночной клуб «Чикаго» – на 6 ящиков меньше, чем магазин «Банановая роща», магазин «Банановая роща» на 2 ящика больше, чем ресторан «Клубничка», кафе «Лакомка» – на 2 ящика больше, чем ночной клуб «Чикаго». Сколько ящиков бананов получило каждое заведение? Ответ Ресторан «Клубничка» – 6 ящиков, кафе «Лакомка» – 4 ящика, магазин «Банановая роща» – 8 ящиков, ночной клуб «Чикаго» – 2 ящика. Максимальное произведениеУсловие Поменяйте цифры местами так, чтобы в результате умножения получилось максимальное произведение. 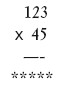 Ответ 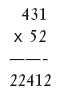 СуммыУсловие Какая сумма из приведенных примеров окажется больше?   Ответ Оба столбца в сумме дают один результат: 1083676269. Окна и зеркалаУсловие Две уборщицы моют 60 окон за 7 часов 20 минут. Сколько времени потребуется им, чтобы вымыть 30 зеркал. Учтите, что все окна и зеркала прямоугольной формы и одинакового размера. Ответ Уборщицам потребуется 1 час 50 минут: зеркала нужно мыть только с одной стороны, а окна с двух. Владелец автосалонаУсловие Владелец автосалона продал два автомобиля: первый с прибылью в 10 %, а второй с убытком в 10 %. В результате этой сделки он получил 5 % прибыли. Во сколько обошелся каждый из автомобилей владельцу магазина, если его прибыль составила 1000 долларов? Ответ Владелец автосалона купил первый автомобиль за 15 000 долларов, а второй – за 5 000 долларов. Его прибыль в первом случае составила 1500 долларов, а во втором убытки составили 500 долларов. Таким образом, чистый доход владельца автосалона составил 1000 долларов или 5 %. НумизматУсловие Нумизмат положил все свои монеты в 4 коробочки, в каждую из которых он поместил одинаковое количество монет одного достоинства. Потом он смешал монеты из 3 коробочек и поделил их на 3 части, снова сложив в коробочки, в каждой из которых оказалось по одинаковому числу монет разного достоинства. Каким минимальным количеством монет обладал нумизмат? Ответ У коллекционера было не менее 60 монет каждого достоинства. Табун лошадейУсловие Отец оставл своим сыновьям в наследство табун лошадей. Старший сын получил 1 лошадь и 1/7 часть всех остальных лошадей, второй – 2 лошади и 1/7 часть всех остальных лошадей, третий – 3 лошади и 1/7 всех остальных лошадей, четвертый – 4 лошади и 1/7 часть всех остальных лошадей и т. д. Таким образом, табун лошадей был разделен между всеми наследниками без остатка. Сколько у отца было сыновей и какова была численность лошадей в табуне? Ответ Сыновей было шесть, а лошадей в табуне – 36. Рваная колода картУсловие Представьте, что некий силач разорвал колоду карт пополам, сложил в стопку две половины, снова разорвал стопку пополам и т. д. Такая процедура была проделана 52 раза, а все полученные кусочки были сложены в стопку. Какой высоты окажется такая стопка? Ответ Высота стопки будет больше расстояния от Земли до Солнца. Сделка фермеровУсловие Один фермер предложил другому купить у него 4 коровы и 3 теленка по цене 370 долларов или 3 коровы и 4 теленка по цене 330 долларов. Сколько стоит одна корова и один теленок? Ответ Корова стоит 70 долларов, а теленок 30 долларов. Строительство котеджаУсловие При строительстве расходы хозяина на 4 маляров и 3 каменщиков составили 37 000 рублей в неделю, а на 3 маляров и 4 каменщиков – 33 000 рублей в неделю. Сколько рублей платил хозяин каждому из мастеров в неделю? Ответ Каждому маляру хозяин платил 7000 рублей в неделю, а каждому каменщику – 3000 рублей в неделю. Три собакиУсловие Если 3 собаки могут съесть 3 больших куска мяса за 3 минуты, то за сколько минут 30 собак управятся с 30 большими кусками мяса? Ответ Если 3 собаки могут за 3 минуты съесть 3 больших куска мяса, то каждой собаке в отдельности на один кусок мяса понадобится 3 минуты. Поэтому 30 собак управятся с 30 кусками мяса за те же 3 минуты. Семья СидоровыхУсловие Всем членам семьи Сидоровых сейчас 77 лет. Состав семьи таков: отец, мать, дочь и сын. Муж старше жены на 3 года, дочь старше сына на 2 года. Четыре года назад всем членам семьи вместе исполнился 61 год. Сколько лет каждому члену семьи? Ответ Отцу – 33 года, матери – 31 год, дочери – 7 лет, сыну – 5 лет. Происшествие на дорогеУсловие Везла бабушка на базар корзину с яйцами, но когда она переходила дорогу, из-за угла неожиданно выехал автомобиль. От испуга старушка уронила корзину, и все яйца разбились. Водитель автомобиля оказался порядочным парнем, предложив бабушке возместить причиненный ущерб, он спросил, сколько яиц было в ее корзине. «Не знаю, сынок, – ответила автомобилисту старушка. – Разложила я яйца на две кучки поровну, осталось одно яйцо. То же самое повторилось, когда я разложила их поровну на четыре, пять и шесть кучек. И только когда я разложила яйца на семь кучек, ни одного не осталось». Сколько яиц было в корзине у бабушки? Ответ 301 яйцо. Числитель и знаменательУсловие Может ли дробь, в которой числитель меньше знаменателя, быть равной дроби, в которой числитель больше знаменателя? Ответ Да. Например: – 3/6 = 5/-10 Букет цветовУсловие Сколько в букете цветов, если все они гвоздики, кроме двух, все они розы, кроме двух, и все они тюльпаны, кроме двух? Ответ В букете 3 цветка: гвоздика, роза и тюльпан. Три ряда чиселУсловие Представлены три ряда чисел. Используя первые два, восстановите третий ряд. Какое число нужно поставить вместо *? 4: 6, 11, 7 3: 8, 4, 12 *: 10, 55, 15 Ответ Вместо звездочки следует поставить число 8. Все числа перед двоеточием получаются путем суммирования трех чисел ряда и деления полученной суммы на первое число ряда. Для третьего ряда будет: (10 + 55 + 15)/10 = 8. Скромное наследствоУсловие Скончавшись, отец семейства оставил своим родным весьма скромное наследство – 7999,68 долларов. Эти деньги согласно завещанию нужно было разделить между его вдовой, 5 сыновьями и 4 дочерями. Он хотел, чтобы каждый сын получил в 3 раза больше того, что должна получить каждая дочь, и чтобы каждая дочь получила в 2 раза больше, чем их мать. Сколько денег должна получить вдова умершего? Ответ Вдова должна получить 205,12 долларов. Это 1/39 всей оставленной в наследство суммы. Коробка елочных шаровУсловие В коробку помещается 60 больших елочных шара красного цвета или 72 маленьких шаров синего цвета. Если в коробку положить 45 красных шаров, сколько синих шаров поместится в коробку? Ответ В коробку можно положить 18 синих шаров, поскольку 3/4 коробки уже занято шарами красного цвета, соответственно, туда можно положить 1/4 от 72 синих шаров. Четыре плотникаУсловие Четыре плотника были наняты, чтобы выполнить определенный объем работы за определенный срок. Каждый из них работал с одинаковой скоростью, однако после первого дня работы два плотника уволились. Два оставшихся плотника могут закончить работу на два дня позже запланированного срока. Сколько дней первоначально отводилось для выполнения всего объема работы? Ответ Работу планировалось выполнить за 3 дня. Рождественские сувенирыУсловие Покупатель приобрел в магазине 2 рождественских сувенира и еще половину всех оставшихся рождественских сувениров. Второй покупатель купил 3 рождественских сувенира и еще 1/3 оставшихся рождественских сувениров. Третий покупатель приобрел 4 рождественских сувенира и еще 1/4 оставшихся рождественских сувениров и т. д. Сколько покупателей уйдут из магазина с рождественскими сувенирами? Ответ С рождественскими сувенирами могут уйти четыре покупателя, поскольку не имеется такого начального числа сувениров, которые позволят в соответствии с условиями пятому покупателю забрать шесть рождественских сувениров и еще 1/6 оставшихся. ГусеницаУсловие В 6 часов утра в воскресенье гусеница начала подниматься по стволу дерева. В течение дня, то есть до 18 часов, она поднималась на высоту 5 м, а в течение ночи спускалась на 2 м. В какой день и час она будет на высоте 9 м? Ответ Довольно часто при решении таких задач рассуждают так: гусеница за 24 часа поднимается на высоту 5 м без 2 м, то есть – на 3 м. Следовательно, высоты 9 м она достигнет по истечении 3 суток – в среду в 6 часов утра. Но этот ответ неверен: в конце вторых суток, то есть во вторник в 6 часов утра, гусеница окажется на высоте 6 м, но в этот же день, начиная с 6 часов утра, она до 18 часов может подняться еще на 5 м. Поэтому на высоте 9 м гусеница окажется во вторник в 13 часов 12 минут. ГрибникиУсловие Отец пошел со своими сыновьями в лес за грибами. В лесу они разошлись в разные стороны и стали искать грибы. Через 30 минут отец сел под дерево отдохнуть и пересчитал найденные грибы: их оказалось 45 штук. Через несколько минут прибежали дети – ни один из них ничего не нашел. Дети попросили отца дать им немного грибов. Он раздал им все свои грибы, затем он и сыновья снова разбрелись в разные стороны. После этого произошло следующее: один мальчик нашел 2 гриба, второй потерял 2 гриба, третий нашел еще столько же, сколько ему дал отец, а четвертый потерял половину полученных от отца грибов. Когда дети пришли домой, оказалось, что у всех них грибов поровну. Сколько каждый из сыновей получил от отца грибов и сколько было у каждого, когда они пришли домой? Ответ Как видно из условия задачи, третьему сыну отец дал грибов меньше всего, поскольку он должен был набрать еще столько же грибов, чтобы сравняться с братьями. Для простоты представим, что третьему сыну отец дал одну горсть грибов. Тогда сколько же таких горстей он дал четвертому сыну? Третий мальчик принес домой две горсти, потому что сам нашел столько же грибов, сколько дал ему отец. Четвертый сын принес домой ровно столько же грибов, сколько и третий мальчик, то есть тоже две горсти. Но, дело в том, что половину своих грибов он потерял по дороге, значит, отец дал ему четыре горсти. Первый сын принес домой две горсти, но из них 2 гриба он нашел сам. Получается, что отец дал ему две горсти без 2 грибов. Второй мальчик принес домой две горсти, но по дороге он потерял 2 гриба – значит, отец дал ему две горсти и еще два гриба. Получается, что отец дал сыновьям одну горсть, четыре горсти, две горсти без 2 грибов и две горсти с 2 грибами, то есть всего девять полных горстей (в двух горстях не хватало 2 гриба, зато в двух других горстях было 2 лишних гриба). Зная первоначальное количество грибов, которые собрал отец, можно сделать вывод, что в каждой горсти было по 5 грибов (45: 9 = 5). Итак, третьему сыну отец дал одну горсть, то есть 5 грибов; четвертому – четыре горсти, то есть 5 х 4 = 20 грибов; первому – две горсти без двух грибов, то есть (5 х 2) – 2 = 8 грибов; второму – две горсти с 2 грибами, то есть (5 х 2) + 2 = 12 грибов. Сумма возрастовУсловие Через 13 лет сумма возрастов детей Ивана Ивановича будет 97. Какая сумма возрастов детей Ивана Ивановича будет через 7 лет? Ответ Сумма возрастов составит 73 года. Четырехзначное числоУсловие Назовите четырехзначное число, в котором первая цифра – треть второй, третья – сумма первых двух, и последняя утроенная вторая? Ответ Это число 1349. Плюс и минусПоставьте вместо звездочек знаки плюс и минус между цифрами так, чтобы получилось верное выражение: 0 * 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 = -1. Ответ Знаки плюс и минус следует поставить следующим образом: 0 + 1 + 2–3 – 4 + 5 + 6–7 – 8 + 9 = -1. Алекс – ЮстасуУсловие Штирлиц должен передать в Центр набор из четырех секретных натуральных чисел А, В, С, D. Для большей секретности он отправил набор чисел А + В, А + С, А + D, В + С, В + D неизвестно в каком порядке.
Центр, получив от Штирлица числа 13, 15, 16, 20, 22, расшифровал сообщение и нашел требуемый набор из четырех секретных натуральных чисел. Какие числа Штирлиц должен был передать в Центр? Ответ Это числа – 6, 7, 9, 13. Поскольку (А + С) + (В + D) = (А + D) + (В + С), а из попарных сумм чисел 13, 15, 16, 20, 22 совпадают только 13 + 22 = 15 + 20 = 35, то А + В = 16, С + D = 19. Поскольку А и В одинаковой четности, то получаем систему двух уравнений с двумя неизвестными: А + В = 16 |A – B| = 2. Решая систему, находим два числа 7 и 9 (то есть А = 7, В = 9 или А = 9, В = 7). Далее легко находим два недостающих числа: 6 и 13. Рыцари и лжецыУсловие Путешественник приехал на остров, каждый из 100 жителей которого или лжец, который всегда обманывает, или рыцарь, который всегда говорит правду. При этом среди жителей острова есть хотя бы один лжец. Лжецы решили лгать таким образом, чтобы каких бы 50 жителей путешественник не собирал вместе, присутствующие среди них лжецы всегда отвечали на вопрос о числе рыцарей среди собранных туземцев так, чтобы путешественник получал один и тот же набор из 50 ответов. Какое наибольшее число рыцарей могло быть на острове? Ответ Решая эту головоломку, нужно рассуждать следующим образом: рыцарей на острове менее 50, иначе путешественник, выбрав всех рыцарей, получил бы 50 ответов «пятьдесят», а, выбрав одного лжеца и 49 рыцарей, услышал бы иной набор ответов. Получается, что лжецов на острове не менее 50 человек. Поскольку набор ответов должен выглядеть правдоподобно, в наборе ответов должен быть 1 ответ «один», 2 ответа «два», 3 ответа «три», 9 ответов «девять» и еще 5 неправдоподобных ответов. Из этого можно сделать вывод, что на острове может быть не больше 9 рыцарей. ДесантУсловие В игре «Десант» две армии захватывают страну. Игроки ходят по очереди, каждым ходом занимая один из свободных городов. Первый город захватывается с воздуха, а каждым следующим ходом можно захватить любой населенный пункт, соединенный дорогой с каким-либо городом, уже занятым этой армией. Если таких городов нет, армия прекращает боевые действия, и игрок считается проигравшим. Постройте такую схему городов и дорог, чтобы игрок, который ходит вторым, смог захватить более половины всех городов, независимо от того, как будет действовать армия его соперника. Ответ Пусть на кольце последовательно расположены точки А1, В2, А3, В1, А2, В3, причем от точек А1, А3, А2 отходят «ветки» с N городами в каждой. Если первый игрок первым ходом занимает точку на ветке, армия второго игрока должна занять соответствующую точку Аi. Если первая армия первым ходом занимает точку Ai, то вторая – Bi. Если первый игрок первым ходом занимает точку Bi, то второй – любую из точек Aj (j не равно i). Дальнейшие действия очевидны. Поскольку в конце игры вторая армия занимает хотя бы две точки Ai, первый игрок захватывает не более, чем n + 3 точек. Поэтому доля городов, захваченных армией второго игрока, не менее (2n + 3)/(3n + 6) > 1/2. В условии задачи вместо 1/2 можно взять любое число, меньшее 2/3 (в этом случае N надо выбирать достаточно большим). ФокусникиУсловие Два фокусника показывают зрителям интересный фокус. Одному из присутствующих они дают колоду карточек с числами от 1 до 78, чтобы он перемешал ее, отобрал любые 40 карточек и отдал их первому фокуснику. Тот выбирает из полученных карточек две и возвращает их зрителю. Последний добавляет к ним одну карточку из своих 38 и, перемешав, отдает эти карточки второму фокуснику, который сразу же показывает, какая из карточек была добавлена в стопку зрителем. Попробуйте разоблачить фокус. Ответ Фокусники любым образом разбивают 78 карточек на 39 групп по две карты и запоминают эту комбинацию. Какие бы 40 карточек зритель не отдал первому фокуснику, среди них обязательно окажутся две карточки из одной пары (поскольку пар всего 39). Первый фокусник должен дать зрителю две карточки из одной пары. Тогда карта, добавленная зрителем, будет из другой пары, ее сможет определить второй фокусник. КладоискателиУсловие Три кладосикателя – Илья, Дмитрий и Алексей – нашли шкатулку, в которой было 6 монет: 3 золотых и 3 серебряных. Кладоискатели перемешали все монеты и по очереди с завязанными глазами вытащили по 2 монеты, не сказав друг другу, кому какие монеты достались. Илья не знает, какие монеты досрались Дмитрию, а какие Алексею, но знает, какие монеты достались ему самому. Придумайте вопрос, на который Илья ответит «да», «нет» или «не знаю», и по ответу на который вы сможете догадаться, какие монеты ему достались. Ответ Вопрос: «Правда ли, что у тебя золотых монет больше, чем у Алексея?». Если у Ильи 2 золотые монеты, он скажет «да», поскольку у Алексея не может быть больше одной золотой монеты. Если обе монеты у Ильи серебряные, а у Алексея хотя бы одна золотая, он ответит «нет». Если же ему достались разные монеты, он ответит «не знаю», так как у Алексея может оказаться как 2 золотые, так и 2 серебряные монеты. Пятидесятикопеечные монетыУсловие В ряд выложили 2001 монету достоинством 5, 10 и 50 копеек. Оказалось, что между любыми двумя пятикопеечными монетами лежит хотя бы одна монета, между двумя десятикопеечными монетами лежат хотя бы две монеты, а между любыми двумя пятидесятикопеечными монетами лежат хотя бы три монеты. Определите, сколько в ряду пятидесятикопеечных монет. Ответ Рассмотрим любые четыре идущие подряд монеты и попробуем доказать, что среди них есть одна пятидесятикопеечная. Если среди них нет пятидесятикопеечной, то пятикопеечные и десятикопеечные монеты чередуются, что невозможно. Двух пятидесятикопеечных монет тоже быть не может, поскольку между ними должно быть хотя бы три монеты. Из этого можно сделать вывод, что среди первых 2000 монет ровно 500 пятидесятикопеечных. Следовательно, всего пятидесятикопеечных монет может быть 500 или 501. Неверные мужьяУсловие В некотором королевстве правил король. Все мужчины этого королевства хорошо разбирались в математике, все они почитали своего короля и выполняли все, что он им прикажет. Король всегда говорил только правду. Все выстрелы в королевстве слышны в каждом доме, а все перечисленные факты известны каждому жителю королевства. Король был озабочен неверностью некоторых жен в королевстве и решил покончить с их изменами раз и навседа. Поэтому он собрал всех женатых мужчин на городской площади и сделал следующее заявление: «Существует по крайней мере одна неверная жена в королевстве. Все женатые мужчины знают о верности или неверности всех чужих жен, но о своей супруге не имеют никакой информации. Я запрещаю вам обсуждать верность своей жены с другими мужчинами. Как только муж узнает, что его жена изменяет ему, он должен застрелить ее в тот же день в полночь». Тридцать девять тихих ночей минуло после речи короля. В сороковую ночь прозвучали выстрелы. Сколько жен было убито? Ответ Обозначим n – число неверных жен. Тогда муж каждой неверной жены знает о существовании (n – 1) неверной жены. Пусть n = 1. Тогда муж этой жены полагает, что все жены верны. Услышав от корял, что существует по крайней мере одна неверная жена – он понимает, что это его супруга, которую он обязан застрелить. Далее пусть n = 2. Мужья этих женщин полагают, что в королевстве есть лишь одна неверная жена и ждут, что ее супруг застрелит ее в первую же ночь. Поскольку убийства не произошло, это значит, что их собственная жена неверна и ее следует застрелить. Действуя далее по индукции, получаем, что n неверных жен будет застрелено в n-ю ночь, то есть в сороковую ночь было убито 40 неверных жен. Адрес СашиУсловие Даша и Наташа хотят отправиться в гости к Саше. Все они живут на одной и той же улице (в разных домах), но Даша и Наташа не знают, где живет Саша. Дома на улице имеют номера от 1 до 99. Даша спросила Сашу: «Верно ли, что номер твоего дома – полный квадрат?». Саша ответил. Затем Даша спросила: «Верно ли, что номер твоего дома больше 50?». Саша ответил. Затем Даша подумала, что она знает адрес Саши и пошла к нему в гости. Оказалось, что она ошиблась, что неудивительно, поскольку Саша ответил правдиво только на второй вопрос. После этого Наташа спросила Сашу: «Верно ли, что номер твоего дома – полный куб?». Саша ответил. Затем Наташа спросила: «Верно ли, что номер твоего дома больше 25?». Саша ответил. Наташа решила, что она знает номер дома Саши и отправилась к нему в гости. Оказалось, что и она ошиблась, поскольку Саша ответил правдиво только на второй вопрос. Определите адрес всех троих друзей, если известно, что номер дома Саши меньше, чем номера домов девушек и что сумма всех трех номеров – удвоенный полный квадрат. Ответ Обозначим Nd, Nn, Ns – номера домов Даши, Наташи и Саши. Очевидно, что Саша ответил Даше оба раза утвердительно. Существует только два квадрата больше 50: 64 и 81 – значит в одном из этих домов живет Даша. Поэтому она и подумала, что Саша живет в другом. Значит, на самом деле, Ns > 50 и Ns не равно 64 и не равно 81; Nd = 64 или Nd = 81. Аналогично Саша ответил Наташе оба раза «да». Существует только два куба больше 25: 27 и 64 – значит в одном из этих домов живет Наташа. Именно поэтому она и подумала, что Саша живет по другому адресу. Учитывая, что Ns > 50 и Ns не равно 64 и не равно 81, получаем Nd = 81, Nn = 64, Ns > 50, Ns < 64. Перебором находим, что Ns = 55 (81 + 64 + 55 = 2 х 102). Получается, что номер дома Даши 81, Наташи – 64, а Саши – 55. ОпечаткаУсловие В одном из учебников по математике написано, что наибольшее известное простое число – это разность 23021377-1. Не опечатка ли это? Ответ Это опечатка. Любая степень числа, оканчивающегося на 1, тоже оканчивается на 1. Поэтому, разность 23021377 – 1 оканчивается на 0 и, следовательно, не является простым числом. ТортУсловие Хозяйка купила торт. К ней может прийти или 10, или 11 гостей. На какое наименьшее число кусков ей необходимо заранее разрезать торт так, чтобы его можно было поделить поровну как между 10, так и между 11 гостями? Ответ Хозяйке следует разрезать торт на 20 кусков. Докажем сначала, что разрезать торт меньше, чем на 20 кусков, не удастся. Если придут 10 человек, то каждый из них должен получить не меньше двух кусков. В самом деле, в противном случае один из 10 гостей получил бы один кусок в 1/10 часть торта, а если бы пришло 11 гостей, то этот кусок нужно было бы дополнительно разрезать. Таким образом, количество кусков не меньше, чем 2 х 10 = 20. Покажем, что 20 кусков торта хватит всем гостям. Разрежем торт на 10 кусков по части и на 10 кусков по 1/110. Если придут 10 гостей, то каждый получит один большой кусок и один маленький – всего + 1/110 = 1/10. Если же придут 11 человек, то 10 из них получат по одному большому куску, а один человек – 10 маленьких кусков. РулеткаУсловие Пьер никогда не проигрывает в рулетку больше четырех раз подряд и никогда не ставит на кон больше 20 долларов. Каким образом он может выиграть 1000 долларов, если в случае выигрыша в рулетку возвращается удвоенная ставка и в самом начале игры у Пьера есть 100 долларов? Ответ Пусть Пьер поставит сначала 1 доллар и, если выиграет, скажет: «Ок'ей» и снова поставит 1 доллар. Если проиграет, то в следующей ставке он ставит 2 доллара. Если выиграет, то его выигрыш покроет предыдущий проигрыш, и по сумме двух ставок он выиграет 1 доллар. После этого пусть Пьер снова скажет: «Ок'ей» и в новой ставке ставит 1 доллар. Если он проиграет и во второй раз, в третий раз он поставит 4 доллара, чтобы в случае выигрыша покрыть предыдущие проигрыши. Если проигрывает в третий раз, то в четвертый раз ставит 8 долларов, если проигрывает и в четвертый, то в пятый раз ставит 16 долларов. По условию он не проигрывает пять раз подряд, значит играя таким образом до первого выигрыша, он заработает 1 доллар не более, чем за 5 ставок. После этого он скажет: «Ок'ей» и будет делать ставки также, как вначале. Получается, что после 1000 «Ок'ей» Пьер выиграет 1000 долларов. Для этого ему потребуется сделать не более 5000 ставок. АльпинистУсловие Альпинисты стоят на горе высотой 100 м. На вершине горы – дерево, на высоте 50 м (посередине горы) – еще одно дерево. У альпиниста есть только 75 м веревки и нож. Может ли он спуститься с горы?
Ответ Альпинисту нужно отрезать 25 м веревки, один конец привязать к дереву на вершине горы, а на другом сделать петлю, через которую следует пропустить оставшиеся 50 м веревки, сложенные вдвое: 25 + 50 х 1/2 = 50, то есть ему как раз хватит веревки, чтобы добраться до дерева, расположенного на высоте 50 м. Далее альпинисту необходимо вытянуть веревку из петли, привязать дереву и спуститься вниз. Можно ли «сотку» разделить на 9?Условие В следующих многозначных числах цифры заменены буквами (одинаковые цифры – одинаковыми буквами, а разные – разными). Оказалось, что слово «девяносто» делится на 90, а «девятка» – на 9. Можно ли «сотку» разделить на 9? Ответ Буква «о» равна нулю. Сумма восьми различных цифр д + е + в + я + н + о + с + т делится на 9. Поскольку сумма всех цифр 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 делится на 9, то сумма двух оставшихся цифр а + к делится на 9. В этом случае слово «сотка» делится на 9 тогда, когда с + т делится на 9 (так как о = 0, а + к делится на 9). С другой стороны, д + е + в + я + т + к + а делится на 9 (д + е + в + я + т делится на 9, н + с делится на 9, так как д + е + в + я + н + о + с + т делится на 9 и о = 0). Из этого можно сделать вывод, что с + т не может делиться на 9, следовательно слово «сотка» тоже на 9 не делится. КлоуныУсловие В шеренгу выстроено n клоунов. На голову каждому надевают колпак одного из цветов: красного, желтого или зеленого. Клоун, стоящий в шеренге n-м видит всех остальных клоунов, n-1-й клоун видит n-2 клоунов, стоящих впереди, ... 2-й клоун видит только первого, первый клоун не видит никого. Цвет своего колпака клоун определить не может. Каждого клоуна по порядку, начиная с n-го, просят ответить, какого цвета у него колпак. Клоун обязан назвать один из трех цветов. Какое максимальное число клонов могут гарантированно угадать цвет своего колпака? При этом клоуны перед опоросом могут договориться, но не могут заранее знать, какие колпаки на них наденут. Ответ Пронумеруем цвета числами от 0 до 2. n-й клоун, видя всех, кроме себя, складывает числа, соответствующие цветам видимых им колпаков, и называет цвет, соответствующий остатку от деления полученной им суммы на 3. n-1-й клоун слышит ответ n-го и видит всех остальных клоунов, кроме себя и n-го. Он также может сложить числа, соответствующие видимым им колпакам и взять остаток от деления на 3. Разность между ответом n-го клоуна и этим числом будет соответствовать цвету колпака на п-1-м клоуне, что даст ему возможность правильно назвать цвет своего колпака. Таким же образом действует и n-2-й клоун, учитывая два предыдущих ответа. Получается, что все клоуны, кроме n-го, гарантированно узнают цвет своего колпака (n-й клоун не может узнать цвет своего колпака, так как его колпак никто не видит). Бесконечные крестики-ноликиУсловие На бесконечной клетчатой бумаге двое играют в крестики-нолики. Один игрок ставит своим ходом два крестика (не обязательно рядом), а другой – один нолик. Сможет ли играющий крестиками поставить 10 крестиков в ряд? Ответ Первые 29 = 512 крестика (за 256 ходов) следует ставить далеко друг от друга (например, на расстоянии 30 клеток друг от друга по горизонтальной прямой). Ответными ходами второй игрок может «испортить» только 256 крестиков, поставив рядом нолик, а 28 = 256 останутся «неиспорченными». Поставив 256 крестиков (за 128 ходов) рядом с каждым «неиспорченным», получим не менее 27 = 128 «неиспорченных» пар. Далее аналогично получаем 26 = 64 «неиспорченных» тройки крестиков, 25 = 32 «неиспорченных» четверки крестиков, 2 «неиспорченных» восьмерки и 1 «неиспорченную» девятку. За один ход второй игрок не сможет закрыть ряд из девяти крестиков с двух сторон. И следующим ходом первый игрок поставит еще один крестик, то есть получит ряд из 10 крестиков. Коммунальная квартираУсловие В коммунальной квартире 10 комнат. Жители этих комнат просыпаются по очереди. Если дверь их комнаты на месте, они снимают дверь какой-либо другой комнаты и относят ее в подвал. Если же дверь их комнаты отсутствует, они забирают из подвала любую дверь и ставят ее на место своей (если ни одно из этих действий невозможно, они не делают ничего). Какое наибольшее количество дверей может оказаться в подвале после того, как все жители комнат проснутся? Ответ Представим, что жильцы коммунальной квартиры просыпаются в порядке нумерации их комнат: сначала – первой, потом – второй и т. д. Рассмотрим комнату, с которой сняли дверь жители первой комнаты. Когда жильцы комнаты со снятой дверью проснутся, они повесят свою дверь на место. В результате этих двух операций ни одной двери в подвале не прибавится и, если даже жильцы остальных восьми комнат снимут по двери, в подвале окажется не более 8 дверей. Например: жители первой комнаты снимают дверь с десятой комнаты, жители второй комнаты снимают дверь с первой, жители n-й комнаты снимают дверь с n – 1 (1 < n < 10) комнаты. Проснувшиеся последними жители десятой комнаты вешают свою дверь на место, после чего в подвале окажется 8 дверей от первой, второй, третьей, четвертой, пятой, шестой, седьмой и восьмой комнат. КонструкторУсловие Никите подарили игру «Конструктор», в которой было 100 деталей разной длины. В инструкции к игре написано, что из любых трех деталей можно составить треугольник. Никита решил проверить это утверждение и стал составлять из деталей треугольники. Детали лежат в наборе по возрастанию длин. Какое наименьшее число проверок необходимо сделать Никите, чтобы доказать или опровергнуть то, что написано в инструкции? Ответ Никите нужна только одна проверка. Ему достаточно проверить, можно ли составить треугольник из двух самых коротких деталей и одной самой длинной. Если треугольник не составляется, то утверждение инструкции опровергнуто. Если же его можно составить, то сумма длин двух самых коротких деталей больше длины самой длинной, а это означает, что из любых деталей можно составить треугольник. Карточный фокусУсловие На одном столе лежат карты, 10 из которых лежат рубашкой вниз. Фокусник с повязкой на глазах подходит к столу, берет несколько карт и перекладывает их на другой стол, при этом, возможно, переворачивая некоторые из них. Такую операцию разрешается повторять несколько раз (можно брать карты как с первого, так и со второго стола). Как переложить карты так, чтобы на обоих столах было одинаковое количество карт, лежащих рубашкой вниз? Ответ Переложим на второй стол 10 карт, переворачивая каждую из них. Предположим, что среди этих карт оказалось n лежащих рубашкой вниз и 10-n лежащих рубашкой вверх. В этом случае после перекладывания на втором столе будет 10-n лежащих рубашкой вниз карт, а на первом столе останется 10-n карт, лежащих рубашкой вниз (было 10 карт, из них n штук переложили). Таким образом, мы получим то, что требуется в условии головоломки. Сто сумасшедших художниковУсловие Сто сумасшедших художников последовательно красят часть стены 100 х 100 клеток в сто цветов, соблюдая единственное правило: в одной строке и в одном столбце не может оказаться 2 клеток одинакового цвета. Смогут ли 99 сумасшедших художников правильно покрасить стену, если первый художник уже покрасил «свои» 100 клеток? Ответ К сожалению, план сумасшедших художников обречен на провал: например, если в первой строке первые 99 клеток покрашены в 99 различных цветов, а последняя клетка второй строки покрашена в сотый цвет. Хоккейный матчУсловие Хоккейный матч между командами «Дружба» и «Мир» закончился со счетом 8: 5. Докажите, что в матче был такой момент, когда «Дружбе» оставалось забить столько голов, сколько «Мир» уже забил к этому времени. Ответ Матч начался с суммарного счета 0, а потом изменялся на единицу и окончательный суммарный счет стал равен 13. Из этого можно сделать вывод, что в матче был такой момент, когда было забито 8 голов. Пусть n голов забил «Мир», тогда 8-n голов забила «Дружба», что и требовалось доказать. Шахматные фигурыУсловие Можно ли расположить шахматные фигуры в клетках доски размером 8 х 8 (в каждой клетке не более одной фигуры) так, чтобы в любых двух столбцах фигур было поровну, а в любых двух строках – разное количество? Ответ Разобьем строки на 4 пары. В каждой паре строк поставим 8 шахматных фигур: n фигур (n – номер пары строк) – в первой строке данной пары и 8-n фигур – во второй строке пары. Причем расположим их в тех столбцах, в которых не стоит фигура из первой строки данной пары. В результате в каждом столбце доски 8 х 8 будет стоять по 4 фигуры (по одной в каждой паре строк), а в 8 строках – 0, 1, 2, 3, 5, 6, 7, 8 фигур. Таким образом, условие задачи выполняется. Вредный старикУсловие При посадке в автобус выстроилась очередь из n пассажиров, у каждого из которых имелся билет на одно из m мест. Первым в очереди стоял вредный старик, который, как только водитель открыл дверь, вбежал в салон и сел на случайное место (возможно, и на свое). После этого пассажиры по очереди заняли свои места. При этом, если место кого-нибудь из пассажиров занято, он садится случайным образом на одно из свободных мест. Какова вероятность того, что последний пассажир займет свое место? Ответ Представим, что при определенном стечении обстоятельств последний пассажир сел не на свое место (такой случай назовем неудачным). Тогда до прихода последнего пассажира его место было занято пассажиром S (S может быть и вредным стариком). У пассажира S был выбор – какое место занять. В рассматриваемом случае он занял место последнего пассажира. Но с этой же вероятностью он мог занять и место вредного старика, тогда в дальнейшем все пассажиры, включая последнего, займут свои собственные места. Получается, что каждому неудачному случаю соответствует удачный, который может произойти с той же вероятностью. Это говорит о том, что в половине случаев распределение пассажиров по местам будет неудачным. Упорядоченные тройкиУсловие Можно ли из любых пяти чисел, написанных в ряд, выбрать три, идущие в порядке убывания или в порядке возрастания? Ответ Предположим, что n и s – наибольшее и наименьшее из написанных чисел. Если между ними есть какое-либо число, то утверждение верно. Если они располагаются рядом, то либо справа, либо слева от них есть еще два числа. Именно они и образуют нужную тройку чисел либо с числом n, либо с числом s. Упорядоченные четверкиУсловие Можно ли из любых девяти различных чисел, написанных в ряд, выбрать четыре, идущих в порядке убывания или возрастания? Ответ Напишем ряд из следующих девяти чисел: 3, 2, 1, 6, 5, 4, 9, 8, 7. Докажем, что никакие четыре числа в этой последовательности не идут ни в порядке возрастания, ни в порядке убывания. Для этого разобьем их на тройки: 321, 654, 987. Если какие-то два числа из этих девяти упорядочены по возрастанию, они будут из разных троек. Поскольку троек всего три, нельзя выбрать более трех цифр, располагающихся в возрастающем порядке. Если же какие-то два числа из этих девяти стоят в убывающем порядке, они обязательно из одной тройки. Поэтому нельзя выбрать более трех чисел, стоящих в убывающем порядке, так как все они должны располагаться в одной тройке. Хитрая последовательность чиселУсловие Продолжите следующую последовательность чисел: 1, 11, 21, 1112, 3112, 211213, 312213, 212223, 114213. Ответ Каждое следующее число описывает предыдущее: в числе была одна единица – 11; две единицы – 21; одна единица, одна двойка – 1112, три единицы, одна двойка – 3112 и т. д. Ошибка журналистаУсловие Главный редактор газеты «Новость дня» Матвей Сигизмундович нашел ошибку в большой статье, которую писали вместе три журналиста: Арнольд Никифорович, Петр Вахтангович и Ричард Львович. На планерке они стали оправдываться. Арнольд Никифорович: 1. «Не я ошибся». 2. «Ошибку допустил Ричард Львович». 3. «Я написал другую часть статьи». Петр Вахтангович: 1. «Ошибся Арнольд Никифорович». 2. «Я знаю, как исправить эту ошибку». 3. «Всем людям свойственно ошибаться». Ричард Львович: 1. «Не я ошибся». 2. «Я с самого начала подозревал, что в статье – ошибка». 3. «Арнольд Никифорович действительно писал другую часть статьи». Ответ Предположим, что ошибку допустил Арнольд Никифорович. Но тогда неверны сразу два его высказывания, что противоречит условию задачи. Предположим, что ошибся Петр Вахтангович. Построим схему, в которой словом «нет» отмечены заведомо ложные в этом случае высказывания, а словом «да» – те, которые могут быть правдивыми. Арнольд Никифорович: 1 – да;2 – нет; 3 – да. Петр Вахтангович: 1 – нет; 2 – да; 3 – да. Ричард Львович: 1 – да; 2 – нет; 3 – да. Схема показывает, что противоречий с условием не возникает, то есть Петр Вахтангович мог ошибиться. Предположим, что ошибся Ричард Львович. Тогда неверно третье высказывание Арнольда Никифоровича (поскольку два первых его высказывания верны), поэтому неверно третье высказывания Ричарда Львовича (оно точно такое же), но тогда верно первое высказывание Ричарда Львовича (только одно из его высказываний – третье – неверно), а это противоречит предположениям. Итак, ошибиться мог только Петр Вахтангович, значит, он это и сделал. ПереправаУсловие Группа туристов ночью подошла к мосту. Павел может перейти его за 1 минуту, Михаил – за 2, Мария – за 5, а Белла – за 10 минут. У них есть только один фонарик. Мост может выдержать только двоих. Как туристы могут перейти мост за 17 минут? При этом, если переходят двое, они идут с меньшей из скоростей. Двигаться по мосту без фонарика нельзя точно так же, как и носить друг друга на руках. Кидаться фонариком тоже нельзя. Ответ Сначала переходят Павел и Михаил (2 минуты). Затем Павел с фонариком возвращается (1 минута). Далее переходят Белла и Мария (10 минут), после чего Михаил с фонариком возвращается (2 минуты). Потом переходят Павел и Михаил (2 минуты). Итого – 17 минут. Число 203Условие Можно ли число 203 представить в виде суммы нескольких натуральных чисел так, чтобы произведение всех этих чисел тоже было равно 203? Ответ Можно: 203 = 7 + 29 + 1 + 1 + ... + 1 = 7 х 29 х 1 х 1 х ... х 1. Бикфордов шнурУсловие Как известно, бикфордов шнур горит неравномерно, но сгорает ровно за 1 минуту. Можно ли с помощью двух таких шнуров отмерить ровно 45 секунд? Ответ Подожжем одновременно один из шнуров с обоих концов и второй – с одного конца.
Первый шнур сгорит через 30 секунд; в этот момент подожжем второй шнур со второго конца. Как не опоздать на работуУсловие Коллектив сотрудников (12 человек) отправился на выходные на турбазу, расположенную в 20 км от места их работы. В понедельник утром они должны были одновременно как можно скорее прибыть на работу. Для этого они остановили такси. «Я еду со скоростью 20 км/час, – сказал водитель, – и могу взять только 4 человека. С какой скоростью вы идете пешком?». Один из сотрудников ответил: «Каждый из нас идет со скоростью 4 км/час». «Отлично!» – воскликнул водитель. – Тогда я поеду с четверыми из вас, подвезу их на какое-то расстояние, затем вернусь и посажу еще четверых, подвезу их и вернусь за остальными. От вас же требуется только одно: все время, пока вы не едете на такси, идти пешком».
Сотрудники отправились в путь ровно в 8 утра. Когда они приедут на работу? Ответ Водитель такси должен подвезти четверых сотрудников на 12 км и высадить в 8 км от работы. Затем ему следует вернуться на 8 км и подобрать еще четверых (из восьми), которые к тому времени как раз окажутся там. Их ему нужно подвезти на 12 км и высадить в 4 км от работы. Затем, вернувшись на 8 км за остальными, которые к тому времени успеют пройти 8 км, отвезти их на 12 км, то есть прямо до места работы. Таким образом весь коллектив сотрудников прибудет на работу одновременно, причем такси пройдет 52 км за 2 и 3/5 часа. Следовательно, сотрудники окажутся на рабочих местах в 10 часов 26 минут. Три воскресеньяУсловие В месяце три воскресенья выпали на четные числа. Какой день недели был седьмого числа этого месяца? Ответ Через семь дней повторяется каждый день недели. Поэтому первые 28 дней содержат четыре понедельника, четыре вторника и т. д. и четыре воскресенья. При этом два воскресенья падают на четные числа, а два – на нечетные. Поэтому третье воскресенье выпадает на 30-е число. Получается, что 2-го числа также было воскресенье, а 7-го числа – пятница. Воздушные шарикиУсловие У Тани и Оксаны есть несколько воздушных шариков, среди которых имеются большие и маленькие, а также красные и зеленые. Докажите, что подруги могут взять по одному шарику так, чтобы они одновременно оказались разного размера и разного цвета. Ответ Предположим, что Таня взяла какой-нибудь большой шарик, а Оксана – маленький. Если эти шарики оказались разных цветов, то задача решена. Пусть шарики оказались одного цвета, например красного. В этом случае по условию задачи среди оставшихся шариков есть зеленый. Если это большой зеленый шарик, пусть его возьмет Таня вместо своего, а если – маленький, пусть его возьмет Оксана. После этого шарики у подруг будут разного цвета и разного размера. АпельсиныУсловие На продуктовом складе апельсины расфасованы в ящики по 24, 23, 17 и 16 кг. Можно ли отправить в магазин со склада 100 кг апельсинов, не раскрывая ящики? Ответ Можно: четыре ящика по 17 кг и два ящика по 16 кг. Рыбаки и щукиУсловие Пять рыбаков съели пять щук за пять дней. За сколько дней десять рыбаков съедят десять щук? Ответ Если пять рыбаков съели пять щук за пять дней, то другие пять рыбаков съедят за те же пять дней еще пять щук. Получается, что десять рыбаков съедят десять щук за пять дней. Баба-яга и тараканыУсловие Все животные Бабы-яги, кроме двух, – жабы, все, кроме двух, – кошки, и все, кроме двух, – вороны. Остальные – тараканы. Сколько тараканов у Бабы-яги? Ответ У Бабы-яги либо два таракана, либо одна кошка, одна жаба и одна ворона. Цыплята и утятаУсловие У цыплят и утят 42 ноги и 12 голов. Сколько цыплят и сколько утят? Ответ 9 цыплят и 3 утенка. Остановившиеся часыУсловие У Ромы нет карманных часов, а только настенные, которые остановились. Он пошел к своему другу Володе, часы которого идут верно, пробыл у него некоторое время и, вернувшись домой, поставил свои часы правильно. Как ему удалось это сделать, если он не знал, сколько времени у него займет дорога от своего дома до дома Володи? Ответ Рома завел остановившиеся часы, пошел к Володе, а, вернувшись, подсчитал время, затраченное на дорогу. Толщина книгиУсловие Известно, что 60 листов книги имеют толщину 1 см. Какова толщина книги, если в ней 240 страниц? Ответ Страниц 240, на каждом листе 2 страницы, значит, всего листов 120: их толщина в 2 раза больше, чем 60, и следовательно, равняется 2 см. Шуточные головоломки на смекалкуЭти головоломки вы можете решать в одиночестве или предложить их в качестве игр для веселой компании. Выигрывает тот, кто первым даст правильный ответ на вопрос. КорабльУсловие Недалеко от берега стоит корабль со спущенной на воду веревочной лестницей вдоль борта. У лестницы 10 ступенек, а расстояние между ними —30 см. Самая нижняя ступенька касается поверхности воды. Начинается прилив, который поднимает воду за каждый час на 15 см. Через сколько времени покроется водой третья ступенька лестницы? Ответ Вода никогда не покроет третью ступеньку, поскольку вместе с водой поднимутся и корабль, и лестница. Жилец с двадцать пятого этажаУсловие Андрей живет на двадцать пятом этаже тридцатиэтажного дома. Каждое утро (кроме субботы и воскресенья) он входит в лифт, спускается вниз и отправляется на работу. Вечером, вернувшись домой, он входит в лифт, поднимается на двадцать четвертый этаж, а оттуда поднимается пешком еще на один этаж. Почему Андрей выходит из лифта на двадцать четвертом этаже? Ответ Он просто не достает до кнопки. ТросУсловие Трос растягивается на 0,5 см от нагрузки в 100 кг. На сколько сантиметров растянется трос от нагрузки в 10 тонн? Ответ Разорвется. Кнопка лифтаУсловие В 9-этажном доме есть лифт. На 1-м этаже живет 5 человек, от этажа к этажу количество жильцов удваивается. Какую кнопку в лифте этого дома нажимают чаще других? Ответ Кнопку первого этажа. Произведение последовательных чиселУсловие Чему равно произведение последовательных целых чисел, начинающихся числом 5 и оканчивающихся числом 5? Ответ Нулю. КрышаУсловие Крыша одного дома несимметрична: один скат ее составляет с горизонталью угол 60°, другой – 70°. Предположим, что селезень снес яйцо на гребень крыши. В какую сторону упадет яйцо – в сторону более пологого или более крутого ската? Ответ Селезни не несут яиц. ЛивеньУсловие Человек попал под ливень, и ему негде и нечем было укрыться. Домой он пришел весь мокрый, но ни один волос на его голове не промок. Почему? Ответ Он был лысым. Красная, черная, белая, зеленаяУсловие Двое гуляющих остановились около одного предмета и заспорили. Один сказал: «Это красная». Второй возразил: «Нет, это черная». «Почему же она белая?» – спросил первый. «А потому, что зеленая». Что это? Ответ Куст смородины. ДвухтомникУсловие На полке рядом стоят два тома одного произведения. Сколько страниц находится между 1-й страницей 1-го тома и последней страницей 2-го тома, если в первом томе 320 страниц, а во втором 290 страниц? Ответ Только 2 обложки, поскольку второй том стоит справа от первого. ТрехтомникУсловие На книжной полке стоит трехтомник. Толщина каждого тома 5 см. Книжный червь прополз от первой страницы первого тома до последней страницы третьего тома (по прямой линии). Какой путь он проделал? Толщиной обложки следует пренебречь. Ответ Первая страница первого тома и последняя страница третьего тома примыкают ко второму тому. Так что путь червяка равен толщине второго тома, то есть составляет 5 см. Два поездаУсловие Один поезд идет из Саратова в Москву, а другой – из Москвы в Саратов. Вышли они одновременно, но скорость первого в три раза больше скорости второго. Какой поезд будет дальше от Москвы в момент встречи? Ответ Поезда будут на одинаковом расстоянии. |
|
|||
|
Главная | В избранное | Наш E-MAIL | Добавить материал | Нашёл ошибку | Наверх |
||||
|
|
||||
